In the debate over the relationship between economy-wide productivity and typical workers’ pay the numbers are clear: typical workers’ pay hasn’t come close to keeping up with productivity, and a wide gap between the two has developed. There has been no credible challenge to this basic finding.

Some have moved past the debate over the numbers to argue that this divergence is not a sign that the economy, and economic policy, is failing these workers. Instead, they argue that the underlying productivity of most workers must have stagnated, and that it is their productivity stagnation that has driven their wage stagnation. This essentially argues that relatively stagnant pay for typical workers is because most Americans are no more productive now than decades ago, and hence did not deserve to see gains in hourly pay in recent decades. A corollary to this argument is the notion that the pay and productivity divergence therefore requires no policy response other than attempting to raise workers’ productivity.

We noted in our recent paper the glaring lack of any actual evidence for the claim that most workers have not become more productive in the past three decades. In fact, most evidence (which we’ll highlight a bit later) indicates that most American workers have become substantially more productive over time. However, in a recent blog post, Evan Soltas claims to have marshalled evidence indicating that most American workers have not seen productivity gains in recent years. Soltas’ conclusion that most American workers must not have become more productive in recent decades is predicated upon looking at industry-level measures of productivity and average pay. He claims to have found a strong correlation between the growth of industry productivity and industry pay, and then claims this (somehow) implies that we know the divergence between economy-wide productivity and typical workers’ pay must, therefore, have been driven by the failure of typical workers to become more productive in recent decades.

We explain in this post why his suggested empirical test for assessing this question is actually meaningless, and will also show how the execution of his test is flawed, and his empirical conclusions (which would be irrelevant in any case) are false. Estimated correctly, there is no correlation between industry productivity and average industry pay. More importantly, even if there was such a correlation, this would be entirely uninformative about the underlying productivity of individuals. In short, Soltas asked the wrong question and then answered it incorrectly.

In what follows, we’ll first demonstrate why his answer is wrong—the empirical claim of a correlation between industry pay and productivity does not exist. Then we’ll explain why the question is wrong—one cannot actually infer anything about the underlying productivity of individuals from industry data.

Wrong answer: there is no link between industry productivity and industry average pay

Soltas describes his data work as using 246 “reasonably granular” industry categories to examine “changes in sector-level labor productivity” and “changes in sector-level hourly labor compensation.” Soltas was kind enough to provide greater detail by email. Our judgment is that his quick and dirty empirical work is fatally flawed along many dimensions and provides no useful information even about the narrow question of industry pay and productivity correlations. Rather than try to fix his analysis we offer two straightforward analyses using the same data series available from BLS, Labor Productivity and Costs by Industry Tables from August 6, 2015.

Here are the major shortcomings of Soltas’ data analysis:

Industry categories: he does not use 246 “granular categories,” he uses every industry category available at every level of aggregation—two, three, four, and five digit. This means that there are observations for a two-digit industry and for underlying three digit industries as well as for three digit industries with some underlying four digit industries. This means he has far fewer truly independent observations than he thinks. It is important to use non-redundant data in such an exercise.

Labor productivity: Soltas does not use the labor productivity measure provided by BLS but instead tries to construct his own. He divides a measure of industry output by the product of total hours worked in an industry and total employment. This is a clear mistake—total hours worked already has total employment embedded in it (it is itself the product of average hours worked multiplied by total employment), and only total hours worked should show up in the denominator of a productivity calculation. We informed Soltas of this mistake and he has revised his data and his results. As will be discussed below, the relationship between industry productivity and compensation growth has been halved using the revised data but Soltas has not revised any of his conclusions.

We should also note that we’re not happy with the industry measure of output used by the BLS labor productivity series, but that’s not Soltas’s problem—that’s a problem with the data. The BLS measure is best thought of as revenue per work hour, with revenue adjusted for changes in inventory and intra-industry sales. They do not provide a value-added measure that takes into account changes in the volume of inputs (from outsourcing overseas or contracting out domestically). In subsequent analysis we will try to measure industry productivity trends using better data.

Nominal values: Soltas’ metrics for labor productivity and compensation are measured in nominal dollars, meaning that he doesn’t account for price changes over time. Nominal measures of productivity (like nominal measures of output) are meaningless. For instance, Zimbabwe’s hyperinflation in the 2000s would have made it far and away the world’s leader in productivity growth if measured by nominal productivity. Productivity is real (inflation-adjusted) value-added generated per hour of work, and productivity experts expend great effort developing (quality-adjusted) prices series to make accurate productivity estimations. This mistake makes his whole exercise invalid.

Starting from Scratch

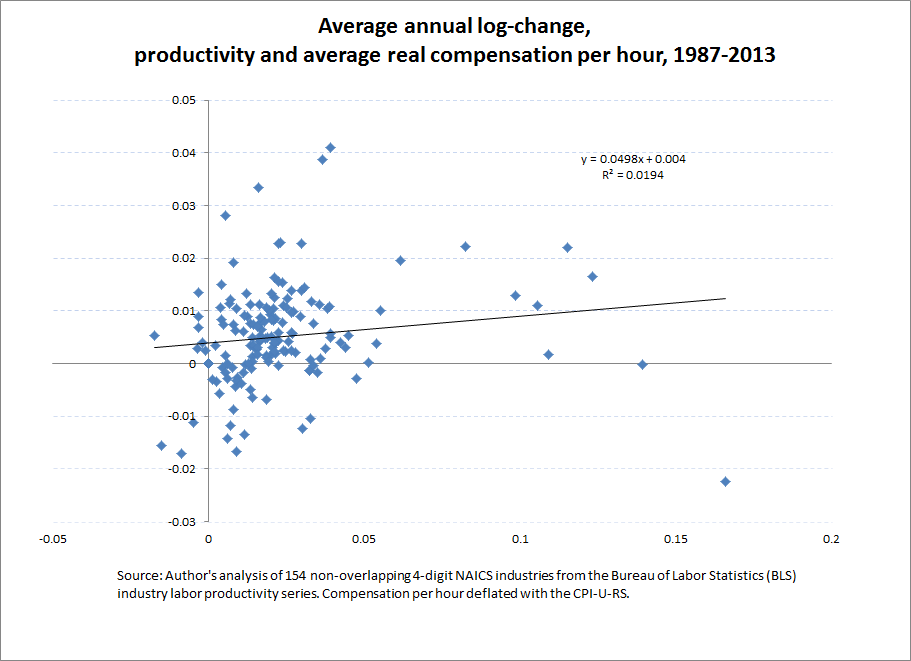
Rather than try to correct Soltas’ data, we provide our own analyses using the same BLS data set. First we replicate his exercise by estimating the relationship between the available measure of hourly productivity and hourly labor compensation deflated (appropriately) by the overall consumer price index. Our sample includes only non-overlapping industries (154 4-digit NAICS codes). The results in Figure A clearly show no relationship between growth in industry productivity and average industry compensation: the coefficient on productivity is near zero and the variation in industry average pay explained by variation in productivity is completely trivial.

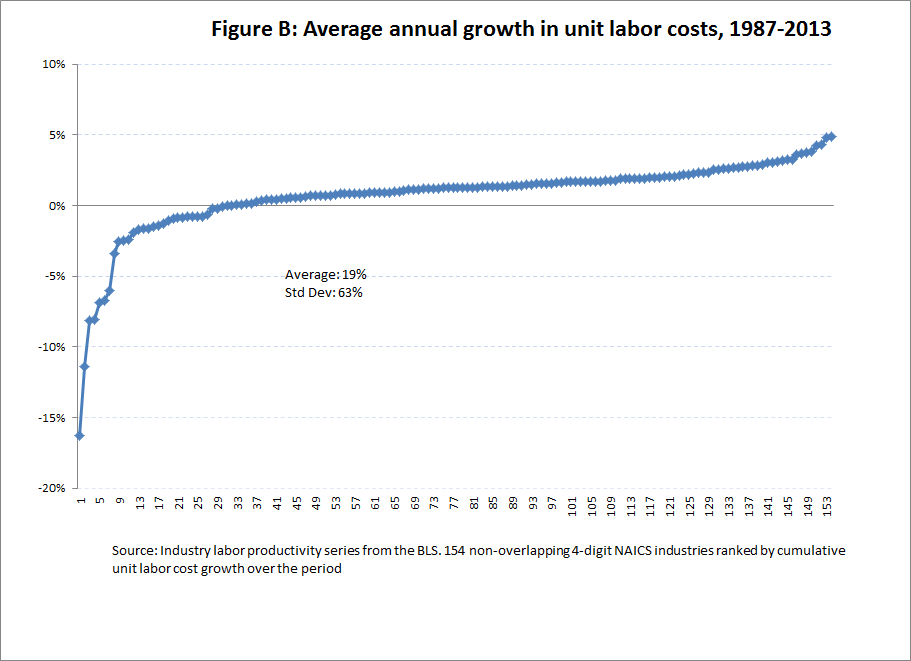
The same point can be made by looking at the change in unit labor costs over time. BLS defines unit labor costs as “a measure that represents the compensation for labor services used to produce each unit of goods and services produced.” Unit labor cost growth is growth in nominal compensation minus the growth of productivity by industry. If there were a strong correlation between pay and productivity at the industry level, unit labor cost growth would be nearly uniform across industries. It’s not —Figure B below shows the distribution of unit labor cost annual rate of growth from 1979 to 2013 across the 160 industries. It runs from strongly negative to very large (more than 100 percent cumulative) increases.

Wrong question: you can’t use industry trends to infer anything about individuals’ productivity

In our recent paper on productivity and pay, we warned precisely about the confusion that Soltas fell into: trying to infer anything about individuals’ productivity from data on industry productivity.

Even if a correlation between productivity and pay growth were found at the industry level, this would not allow you to infer anything about the productivity of individual workers. An industry link between productivity and pay would be an interesting heterodox result. Soltas somewhat oddly thinks that such a link is indicative of the “classical” view of labor markets. It’s not. Instead, it would indicate that something (monopoly profits? unionization?) was allowing workers to capture more of the industry productivity gains than textbook labor market models would indicate is possible. For those more convinced by an appeal to authority, here’s noted labor market expert Alan Manning in Chapter 8 of his book Monopsony in Motion on what the “classical” view of labor markets argues:

In a competitive labor market [ed notes: in the “classical” view] wages should, after controlling for other relevant characteristics of the worker, only be related to employer and job characteristics to the extent that they affect the non-pecuniary aspects of the job…

But heterodox or not (and true or not), there is nothing about an industry-level correlation between productivity and pay that would allow one to conclude that most workers in the U.S. economy had not improved their underlying productivity in recent decades. For example, say that industries that increased their share of highly credentialed workers in recent decades saw both faster productivity growth and higher pay, simply through compositional effects. That is, assume that more highly-credentialed workers are both more productive and more highly paid than other workers. Hence industries that saw an increasing share of highly-credentialed workers over time would see industry-level pay and industry productivity both rise. But a correlation driven by this compositional effect would tell us nothing at all about whether or not the underlying productivity of less-credentialed workers has risen or not. So even if Soltas’s finding that productivity and pay changes over time were correlated at the industry-level was correct (and it’s not, as we’ve shown before), this would go nowhere in proving that most American workers’ productivity have not grown in recent decades.

It’s probably also worth noting that Soltas’s measure of industry pay is average compensation per hour. But one of the main points of our aggregate productivity/pay analysis is that the growth in pay of most American workers has actually lagged far behind growth in average pay. Average pay includes the compensation of a small sliver of workers (especially corporate managers and finance sector professionals) that have seen stratospheric growth rates over the past generation. If this wedge between growth in average pay and the pay of most workers holds across industries (i.e., compensation inequality is pervasive within industries), then this is just one more reason why examining industry level correlations between average pay and productivity are uninformative.

Given that one cannot infer anything from industry trends, it’s important to recognize why most of the relevant evidence actually points to thinking that most American workers have become significantly more productive over time. For one, simple capital-deepening (workers having more and better equipment to do their jobs) and growth in multi-factor productivity (technological and efficiency improvements) have accounted for lots of overall productivity growth in recent decades. Absent strong direct evidence otherwise, these influences should have helped both credentialed and non-credentialed labor alike. Doctors have better imaging machines than 30 years ago while cashiers have better registers and scanners and both have benefited from overall technological improvements. Besides these two influences (capital-deepening and multi-factor productivity), the major influence on productivity growth is “labor quality”. On this, we know that most American workers—and particularly those in the bottom fifth of the wage distribution—have become significantly older and better-educated over time (with education and potential experience being two of the better empirical proxies for productivity) and that “labor quality” grew as strongly in the last forty years as in the earlier post-war period. Moreover, we noted that to believe that pay lags average productivity because the workers productivity itself lags would need to apply to an implausibly large group, since pay lagged productivity 1979-2013 period for ninety to ninety-five percent of the workforce.

Finally, setting aside the meaninglessness of the entire empirical exercise for a moment, one should wonder about Soltas’s interpretation of his results—and how it changes (or doesn’t) when the magnitude of his result is cut in half. As noted above, Soltas revised his results in response to our pointing out his error in computing hours worked. The initial results were: “A one-percentage point increase in productivity generated a 0.81-percentage-point increase in compensation [and explains 74 percent of the variance].” His revised results showed a significantly  smaller correlation between productivity and pay (though obviously still too large, as our results above showed): “A one-percentage point increase in productivity generated a 0.41-percentage-point increase in compensation [and explains 35 percent of the variance].”

Yet his conclusion is unchanged following this large change in the magnitude of his estimated effect: “If labor productivity predicts labor compensation, then it seems fair to say that, at the industry level, workers have been compensated for their productivity gains.”

Soltas never explains why a 0.41 growth in compensation for every percentage rise in productivity implies workers at the industry level are “being compensated” for their productivity. It does not.

Summing up

A key warning of our earlier paper—that one cannot use industry trends to infer anything about individuals’ productivity—remains true. Anybody who looks at industry-level correlations between productivity and average pay and thinks that they’re informative about the question  of whether or not most American workers have become more productive in recent decades is misunderstanding economic theory. Anybody who thinks that “classical” labor market theory predicts a relationship between industry-level productivity and average pay is also misunderstanding this theory.

To be clear, we hold no particular brief for this classical theory—we think there’s lots of power being exercised all over the labor market and would not be surprised if institutions and other influences did actually let workers (or their managers or capital-owners) in some industry capture a greater share of industry productivity gains than textbook theory would indicate. We just know that this remains irrelevant to the question of whether or not most American workers have become more productive over time. And crucially, this is not some heterodox proposition—this irrelevance is also true even if one believes in “classical” labor market theory.