Economic Indicators State jobs and unemployment
Each month, the Bureau of Labor Statistics releases data on employment, unemployment, and the labor force for all states in the previous month. These measures are important indicators of state labor market health. The unemployment rate is the share of the state’s labor force that is not currently employed and is actively looking for work. Healthy job growth is growth that provides employment for all individuals wanting a job. A growing labor force means more people working or seeking jobs. The map and charts below help us understand state labor market conditions, and how states are faring relative to their neighbors and the country as a whole.
State labor market measures are more volatile than national estimates. For this reason, it’s generally better to look at changes over a three, six, or twelve-month period. Month-to-month changes may not be reflective of the underlying trends. For August 2020, we are making an exception to look at the six month change since February 2020, to analyze the economic effect of the coronavirus pandemic.
Key numbers • July 2023
July 2023
Charting jobs, unemployment, and labor force changes across the states and over time
The map below shows the current unemployment rate in each state, and the percent change in the number of jobs in each state over the preceding 12 months. Clicking on a state will also show the change in that state’s unemployment rate or change in the number of jobs over the last 3 months, 12 months, and since December 2007—the peak of the previous business cycle.
The charts below the map show the unemployment rate over time, the change in the total number of jobs since December 2007, and the change in the labor force since December 2007 for the selected state, as well as all other states in the same Census division.
Current state unemployment rate and percent change in total number of jobs over last 12 months
| State | Current unemployment rate | Change in unemployment rate in last 3 months | Change in unemployment rate in last 12 months | Change in unemployment rate since February 2020 | State unemployment rate raking from lowest to highest | Percent change in number of jobs in last 12 months | Change in number of jobs in last 12 months | Percent change in numbers of jobs in last 3 months | Change in number of jobs in last 3 months | Percent change in number of jobs since February 2020 | Change in number of jobs since February 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alabama | 2.1% | -0.1% | -0.5% | -1.3% | 7 | 2.0% | 42500 | 0.7% | 14300 | 3.5% | 72800 |
| Alaska | 3.8% | 0.1% | 0.0% | -1.4% | 43 | 1.6% | 5200 | -0.1% | -400 | -1.5% | -4800 |
| Arizona | 3.6% | 0.2% | -0.3% | -1.4% | 41 | 1.8% | 56600 | 0.1% | 3700 | 5.4% | 162300 |
| Arkansas | 2.6% | -0.2% | -0.7% | -1.0% | 14 | 1.8% | 24300 | 0.6% | 8200 | 5.3% | 68800 |
| California | 4.6% | 0.1% | 0.8% | 0.5% | 49 | 2.0% | 363600 | 0.4% | 76000 | 2.4% | 424200 |
| Colorado | 2.9% | 0.1% | 0.2% | 0.1% | 23 | 1.4% | 38800 | 0.4% | 11200 | 3.1% | 88200 |
| Connecticut | 3.6% | -0.2% | -0.4% | 0.2% | 40 | 1.3% | 21400 | 0.3% | 5700 | -0.4% | -6800 |
| Delaware | 4.1% | -0.2% | -0.3% | 0.4% | 48 | 2.4% | 11200 | -0.1% | -400 | 3.0% | 14200 |
| Washington D.C. | 5.0% | 0.0% | 0.9% | -0.4% | 50 | 0.9% | 6600 | 0.3% | 2200 | -3.8% | -30400 |
| Florida | 2.7% | 0.1% | 0.0% | 0.0% | 19 | 3.2% | 300600 | 0.6% | 63000 | 7.7% | 696100 |
| Georgia | 3.2% | 0.1% | 0.2% | -0.4% | 29 | 1.8% | 88300 | 0.3% | 14400 | 5.2% | 241900 |
| Hawaii | 2.8% | -0.5% | -0.7% | 0.6% | 22 | 2.0% | 12700 | 0.8% | 4900 | -4.1% | -27500 |
| Idaho | 2.8% | 0.2% | 0.1% | -0.2% | 21 | 2.8% | 23600 | 0.8% | 6800 | 10.2% | 78800 |
| Illinois | 4.0% | -0.2% | -0.4% | 0.2% | 46 | 1.5% | 89700 | 0.4% | 26300 | 0.1% | 8900 |
| Indiana | 3.3% | 0.3% | 0.3% | -0.1% | 32 | 1.8% | 57500 | 0.3% | 10500 | 3.1% | 98900 |
| Iowa | 2.7% | 0.0% | -0.1% | 0.1% | 18 | 0.9% | 14400 | -0.7% | -11200 | -0.3% | -5100 |
| Kansas | 2.7% | -0.2% | 0.0% | -0.4% | 17 | 1.6% | 23100 | 0.2% | 2600 | 1.1% | 16200 |
| Kentucky | 3.8% | 0.1% | -0.1% | -0.3% | 42 | 2.6% | 50200 | 0.5% | 10400 | 2.8% | 54100 |
| Louisiana | 3.4% | -0.2% | -0.1% | -1.8% | 35 | 1.6% | 30200 | -0.1% | -1400 | -1.8% | -36400 |
| Maine | 2.4% | 0.0% | -0.3% | -0.4% | 9 | 0.5% | 3200 | -0.4% | -2500 | 0.5% | 3100 |
| Maryland | 1.8% | -0.7% | -1.4% | -2.4% | 3 | 0.8% | 21100 | 0.2% | 5800 | -1.4% | -39500 |
| Massachusetts | 2.5% | -0.6% | -1.2% | -0.4% | 12 | 2.4% | 90300 | 0.6% | 21200 | 1.1% | 41100 |
| Michigan | 3.6% | -0.2% | -0.5% | -0.2% | 39 | 1.4% | 63100 | 0.3% | 13600 | -0.3% | -13500 |
| Minnesota | 3.0% | 0.2% | 0.4% | -0.9% | 26 | 1.4% | 41200 | 0.1% | 3600 | -0.4% | -12900 |
| Mississippi | 3.0% | -0.4% | -0.8% | -2.7% | 25 | 0.3% | 3200 | -0.4% | -5000 | 0.9% | 11000 |
| Missouri | 2.7% | 0.2% | 0.5% | -0.6% | 16 | 2.0% | 58900 | 0.9% | 27200 | 2.6% | 75800 |
| Montana | 2.5% | 0.2% | -0.2% | -1.2% | 11 | 0.5% | 2700 | -0.4% | -2300 | 5.2% | 25400 |
| Nebraska | 2.0% | 0.0% | -0.4% | -1.0% | 6 | 2.0% | 20100 | 0.3% | 3600 | 1.3% | 13800 |
| Nevada | 5.3% | -0.1% | 0.0% | 1.3% | 51 | 3.8% | 56500 | 0.7% | 10600 | 6.9% | 100400 |
| New Hampshire | 1.7% | -0.4% | -0.8% | -1.0% | 1 | 1.5% | 10400 | -0.2% | -1300 | 1.2% | 8600 |
| New Jersey | 3.9% | 0.4% | 0.7% | 0.4% | 45 | 1.7% | 73300 | 0.2% | 9100 | 2.5% | 106700 |
| New Mexico | 3.6% | 0.1% | 0.0% | -1.8% | 38 | 2.6% | 21700 | 0.6% | 5100 | 1.0% | 8900 |
| New York | 3.9% | -0.1% | -0.1% | 0.0% | 44 | 1.3% | 124900 | 0.4% | 35600 | -1.4% | -142100 |
| North Carolina | 3.3% | -0.1% | -0.4% | -0.4% | 31 | 2.2% | 108000 | 0.7% | 33300 | 6.7% | 308000 |
| North Dakota | 2.0% | -0.1% | 0.0% | -0.2% | 5 | 2.0% | 8800 | 1.0% | 4500 | -0.5% | -2300 |
| Ohio | 3.3% | -0.4% | -0.7% | -1.3% | 30 | 1.6% | 89200 | 0.6% | 31200 | 0.5% | 25400 |
| Oklahoma | 2.7% | -0.2% | -0.4% | -0.5% | 15 | 1.7% | 28400 | 0.4% | 6700 | 1.7% | 29800 |
| Oregon | 3.4% | -0.6% | -0.7% | 0.0% | 34 | 2.6% | 49900 | 0.8% | 16700 | 1.7% | 33300 |
| Pennsylvania | 3.5% | -0.6% | -0.8% | -1.5% | 36 | 2.4% | 143100 | 0.6% | 34400 | 0.9% | 53300 |
| Rhode Island | 2.8% | -0.2% | -0.4% | -0.9% | 20 | -1.1% | -5600 | -0.4% | -1900 | -2.8% | -14200 |
| South Carolina | 3.1% | 0.0% | -0.1% | 0.2% | 28 | 2.3% | 52900 | 0.6% | 14300 | 4.9% | 108500 |
| South Dakota | 1.9% | 0.0% | -0.2% | -0.7% | 4 | 1.6% | 7400 | -0.1% | -300 | 4.0% | 17600 |
| Tennessee | 3.1% | -0.2% | -0.2% | -0.5% | 27 | 2.2% | 72400 | 0.6% | 19600 | 5.6% | 175200 |
| Texas | 4.1% | 0.1% | 0.3% | 0.6% | 47 | 3.3% | 441700 | 0.7% | 101400 | 7.7% | 1002900 |
| Utah | 2.4% | 0.1% | 0.1% | -0.2% | 8 | 2.4% | 40700 | 0.3% | 4900 | 9.6% | 151000 |
| Vermont | 1.8% | -0.6% | -0.7% | -0.8% | 2 | 0.7% | 2100 | -0.4% | -1300 | -2.4% | -7500 |
| Virginia | 2.5% | -0.6% | -0.1% | -0.2% | 10 | 1.6% | 64400 | 0.2% | 7100 | 1.3% | 54400 |
| Washington | 3.6% | -0.7% | -0.5% | -0.3% | 37 | 2.6% | 92500 | 0.3% | 11400 | 3.3% | 117800 |
| West Virginia | 3.4% | 0.1% | -0.6% | -1.7% | 33 | 1.0% | 6800 | 0.3% | 2100 | -2.8% | -20200 |
| Wisconsin | 2.6% | 0.2% | -0.4% | -0.4% | 13 | 1.3% | 39500 | 0.2% | 5300 | 0.4% | 11300 |
| Wyoming | 3.0% | -0.5% | -0.5% | -1.9% | 24 | 2.2% | 6200 | 0.8% | 2200 | 0.5% | 1400 |
Jobs refers to the total number of jobs, part-time or full-time, in nonfarm establishments.
Source: EPI analysis of Bureau of Labor Statistics' Local Area Unemployment Statistics data.
State unemployment rates since January 2007: Choose a state to show the unemployment rate over time for that state and all other states in the same Census division. (The dashed line shows the national unemployment rate.)
| date | United States | Alabama | Alaska | Arizona | Arkansas | California | Colorado | Connecticut | Delaware | District of Columbia | Florida | Georgia | Hawaii | Idaho | Illinois | Indiana | Iowa | Kansas | Kentucky | Louisiana | Maine | Maryland | Massachusetts | Michigan | Minnesota | Mississippi | Missouri | Montana | Nebraska | Nevada | New Hampshire | New Jersey | New Mexico | New York | North Carolina | North Dakota | Ohio | Oklahoma | Oregon | Pennsylvania | Rhode Island | South Carolina | South Dakota | Tennessee | Texas | Utah | Vermont | Virginia | Washington | West Virginia | Wisconsin | Wyoming |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007-01-01 | 4.6% | 3.8% | 6.3% | 3.9% | 5.3% | 4.9% | 3.7% | 4.3% | 3.6% | 6.1% | 2.7% | 4.8% | 2.4% | 3.0% | 4.6% | 4.7% | 3.7% | 4.2% | 5.5% | 4.1% | 4.6% | 4.0% | 4.6% | 7.0% | 4.4% | 6.4% | 4.8% | 2.9% | 2.9% | 4.1% | 3.7% | 4.1% | 3.7% | 4.2% | 5.0% | 3.0% | 5.4% | 4.1% | 5.1% | 4.4% | 4.8% | 6.4% | 2.9% | 4.6% | 4.5% | 2.4% | 3.9% | 3.2% | 4.7% | 5.0% | 4.8% | 2.7% |
| 2007-02-01 | 4.5% | 3.8% | 6.2% | 3.9% | 5.3% | 5.0% | 3.5% | 4.3% | 3.6% | 6.1% | 2.8% | 4.7% | 2.4% | 2.9% | 4.6% | 4.6% | 3.7% | 4.2% | 5.4% | 4.2% | 4.6% | 3.9% | 4.6% | 6.9% | 4.4% | 6.4% | 4.8% | 2.8% | 2.8% | 4.2% | 3.7% | 4.1% | 3.7% | 4.2% | 4.9% | 3.0% | 5.5% | 4.1% | 5.0% | 4.4% | 4.7% | 6.3% | 2.9% | 4.5% | 4.4% | 2.4% | 3.9% | 3.2% | 4.6% | 4.9% | 4.8% | 2.6% |
| 2007-03-01 | 4.4% | 3.9% | 6.2% | 3.8% | 5.3% | 5.0% | 3.5% | 4.3% | 3.6% | 6.0% | 2.9% | 4.7% | 2.5% | 2.9% | 4.7% | 4.5% | 3.7% | 4.2% | 5.3% | 4.2% | 4.6% | 3.8% | 4.5% | 6.9% | 4.4% | 6.3% | 4.8% | 2.9% | 2.8% | 4.2% | 3.7% | 4.1% | 3.6% | 4.2% | 4.9% | 3.0% | 5.5% | 4.1% | 5.0% | 4.4% | 4.7% | 6.2% | 2.8% | 4.4% | 4.4% | 2.4% | 3.9% | 3.1% | 4.5% | 4.8% | 4.8% | 2.6% |
| 2007-04-01 | 4.5% | 3.9% | 6.2% | 3.7% | 5.3% | 5.1% | 3.4% | 4.3% | 3.6% | 5.9% | 3.0% | 4.7% | 2.6% | 2.8% | 4.8% | 4.5% | 3.7% | 4.2% | 5.3% | 4.3% | 4.6% | 3.7% | 4.5% | 6.9% | 4.4% | 6.3% | 4.9% | 3.0% | 2.8% | 4.3% | 3.6% | 4.1% | 3.6% | 4.3% | 4.9% | 3.0% | 5.5% | 4.1% | 5.0% | 4.4% | 4.7% | 6.1% | 2.8% | 4.3% | 4.3% | 2.4% | 3.9% | 3.1% | 4.5% | 4.8% | 4.8% | 2.6% |
| 2007-05-01 | 4.4% | 3.9% | 6.2% | 3.6% | 5.4% | 5.1% | 3.4% | 4.3% | 3.6% | 5.9% | 3.1% | 4.8% | 2.6% | 2.8% | 4.9% | 4.5% | 3.7% | 4.2% | 5.3% | 4.3% | 4.6% | 3.7% | 4.5% | 6.9% | 4.5% | 6.2% | 4.9% | 3.2% | 2.9% | 4.4% | 3.6% | 4.1% | 3.5% | 4.3% | 4.9% | 3.0% | 5.6% | 4.1% | 5.0% | 4.4% | 4.8% | 6.0% | 2.8% | 4.3% | 4.3% | 2.5% | 3.9% | 3.1% | 4.5% | 4.7% | 4.8% | 2.7% |
| 2007-06-01 | 4.6% | 4.0% | 6.3% | 3.5% | 5.5% | 5.2% | 3.5% | 4.4% | 3.5% | 5.9% | 3.2% | 4.8% | 2.7% | 2.9% | 5.0% | 4.5% | 3.7% | 4.2% | 5.3% | 4.2% | 4.7% | 3.7% | 4.5% | 7.0% | 4.6% | 6.1% | 5.0% | 3.3% | 2.9% | 4.5% | 3.5% | 4.1% | 3.5% | 4.4% | 5.0% | 3.0% | 5.6% | 4.0% | 5.1% | 4.5% | 4.9% | 6.0% | 2.8% | 4.3% | 4.3% | 2.5% | 3.9% | 3.2% | 4.5% | 4.7% | 4.8% | 2.7% |
| 2007-07-01 | 4.7% | 4.0% | 6.3% | 3.5% | 5.5% | 5.3% | 3.6% | 4.4% | 3.5% | 5.9% | 3.3% | 4.9% | 2.7% | 3.0% | 5.1% | 4.5% | 3.7% | 4.2% | 5.3% | 4.1% | 4.7% | 3.7% | 4.5% | 7.1% | 4.6% | 6.1% | 5.1% | 3.5% | 3.0% | 4.6% | 3.5% | 4.2% | 3.5% | 4.5% | 5.1% | 3.0% | 5.7% | 4.0% | 5.2% | 4.5% | 5.0% | 5.9% | 2.8% | 4.5% | 4.3% | 2.6% | 3.9% | 3.2% | 4.6% | 4.8% | 4.9% | 2.8% |
| 2007-08-01 | 4.6% | 4.1% | 6.3% | 3.5% | 5.5% | 5.4% | 3.7% | 4.5% | 3.5% | 5.9% | 3.4% | 4.9% | 2.8% | 3.1% | 5.2% | 4.6% | 3.7% | 4.2% | 5.4% | 4.0% | 4.8% | 3.7% | 4.5% | 7.2% | 4.7% | 6.0% | 5.2% | 3.6% | 3.0% | 4.7% | 3.4% | 4.2% | 3.5% | 4.5% | 5.2% | 3.1% | 5.7% | 4.0% | 5.3% | 4.6% | 5.2% | 6.0% | 2.9% | 4.6% | 4.3% | 2.6% | 4.0% | 3.3% | 4.6% | 4.8% | 4.9% | 2.8% |
| 2007-09-01 | 4.7% | 4.2% | 6.3% | 3.7% | 5.5% | 5.5% | 3.9% | 4.6% | 3.6% | 5.9% | 3.6% | 5.0% | 2.9% | 3.2% | 5.3% | 4.7% | 3.8% | 4.3% | 5.4% | 3.9% | 4.8% | 3.7% | 4.5% | 7.3% | 4.7% | 6.0% | 5.3% | 3.7% | 3.0% | 4.8% | 3.4% | 4.3% | 3.5% | 4.6% | 5.3% | 3.1% | 5.7% | 3.9% | 5.3% | 4.7% | 5.4% | 6.0% | 2.9% | 4.8% | 4.4% | 2.6% | 4.0% | 3.4% | 4.7% | 4.9% | 4.9% | 2.8% |
| 2007-10-01 | 4.7% | 4.2% | 6.3% | 3.8% | 5.5% | 5.7% | 4.0% | 4.6% | 3.7% | 5.9% | 3.7% | 5.1% | 3.0% | 3.3% | 5.5% | 4.8% | 3.8% | 4.3% | 5.4% | 3.9% | 4.8% | 3.7% | 4.5% | 7.3% | 4.8% | 6.0% | 5.4% | 3.8% | 3.0% | 5.0% | 3.4% | 4.3% | 3.6% | 4.6% | 5.3% | 3.0% | 5.7% | 3.9% | 5.4% | 4.8% | 5.5% | 6.0% | 2.8% | 5.0% | 4.4% | 2.7% | 4.0% | 3.5% | 4.7% | 4.9% | 4.9% | 2.7% |
| 2007-11-01 | 4.7% | 4.3% | 6.3% | 4.0% | 5.4% | 5.7% | 4.1% | 4.7% | 3.7% | 5.9% | 3.9% | 5.2% | 3.0% | 3.2% | 5.5% | 4.8% | 3.7% | 4.3% | 5.4% | 3.9% | 4.8% | 3.6% | 4.5% | 7.3% | 4.8% | 6.0% | 5.4% | 3.8% | 3.0% | 5.1% | 3.4% | 4.4% | 3.7% | 4.7% | 5.3% | 3.0% | 5.7% | 3.7% | 5.3% | 4.8% | 5.7% | 6.0% | 2.8% | 5.1% | 4.4% | 2.8% | 4.0% | 3.5% | 4.7% | 4.8% | 4.8% | 2.7% |
| 2007-12-01 | 5.0% | 4.4% | 6.2% | 4.1% | 5.2% | 5.8% | 4.1% | 4.7% | 3.8% | 6.0% | 4.0% | 5.3% | 3.1% | 3.2% | 5.6% | 4.8% | 3.7% | 4.3% | 5.4% | 4.0% | 4.7% | 3.6% | 4.5% | 7.2% | 4.7% | 6.0% | 5.4% | 3.8% | 3.0% | 5.2% | 3.4% | 4.5% | 3.7% | 4.7% | 5.3% | 3.0% | 5.7% | 3.6% | 5.2% | 4.8% | 5.9% | 5.9% | 2.7% | 5.2% | 4.4% | 2.8% | 4.0% | 3.6% | 4.6% | 4.8% | 4.7% | 2.6% |
| 2008-01-01 | 5.0% | 4.5% | 6.2% | 4.3% | 5.1% | 5.9% | 4.2% | 4.8% | 3.9% | 6.0% | 4.2% | 5.5% | 3.1% | 3.1% | 5.6% | 4.8% | 3.7% | 4.3% | 5.3% | 4.1% | 4.6% | 3.6% | 4.5% | 7.2% | 4.7% | 6.0% | 5.4% | 3.8% | 2.9% | 5.3% | 3.4% | 4.6% | 3.8% | 4.7% | 5.2% | 2.9% | 5.6% | 3.4% | 5.1% | 4.8% | 6.0% | 6.0% | 2.6% | 5.3% | 4.3% | 2.8% | 4.0% | 3.6% | 4.6% | 4.7% | 4.5% | 2.6% |
| 2008-02-01 | 4.9% | 4.7% | 6.2% | 4.4% | 5.0% | 6.0% | 4.2% | 4.9% | 4.0% | 6.1% | 4.4% | 5.6% | 3.1% | 3.1% | 5.7% | 4.8% | 3.7% | 4.2% | 5.4% | 4.1% | 4.6% | 3.6% | 4.6% | 7.2% | 4.7% | 6.1% | 5.4% | 3.9% | 2.9% | 5.5% | 3.4% | 4.6% | 3.8% | 4.8% | 5.2% | 2.8% | 5.6% | 3.3% | 5.1% | 4.8% | 6.2% | 6.0% | 2.6% | 5.4% | 4.3% | 2.9% | 4.1% | 3.7% | 4.6% | 4.6% | 4.4% | 2.6% |
| 2008-03-01 | 5.1% | 4.9% | 6.3% | 4.6% | 4.9% | 6.2% | 4.3% | 5.0% | 4.1% | 6.2% | 4.6% | 5.8% | 3.2% | 3.2% | 5.8% | 4.9% | 3.7% | 4.2% | 5.5% | 4.1% | 4.7% | 3.7% | 4.6% | 7.3% | 4.8% | 6.1% | 5.5% | 4.0% | 3.0% | 5.7% | 3.4% | 4.7% | 3.8% | 4.8% | 5.2% | 2.8% | 5.7% | 3.2% | 5.1% | 4.9% | 6.4% | 6.1% | 2.6% | 5.6% | 4.3% | 2.9% | 4.2% | 3.7% | 4.7% | 4.5% | 4.3% | 2.6% |
| 2008-04-01 | 5.0% | 5.1% | 6.3% | 4.9% | 5.0% | 6.4% | 4.4% | 5.1% | 4.2% | 6.3% | 4.9% | 6.0% | 3.4% | 4.1% | 5.9% | 5.1% | 3.8% | 4.2% | 5.6% | 4.2% | 4.8% | 3.8% | 4.8% | 7.4% | 4.9% | 6.3% | 5.6% | 4.1% | 3.0% | 5.9% | 3.5% | 4.8% | 3.9% | 4.9% | 5.3% | 2.9% | 5.9% | 3.2% | 5.2% | 4.9% | 6.6% | 6.3% | 2.7% | 5.8% | 4.4% | 3.0% | 4.2% | 3.9% | 4.8% | 4.4% | 4.4% | 2.6% |
| 2008-05-01 | 5.4% | 5.3% | 6.4% | 5.2% | 5.0% | 6.7% | 4.5% | 5.3% | 4.5% | 6.4% | 5.2% | 6.2% | 3.6% | 4.7% | 6.1% | 5.3% | 3.9% | 4.3% | 5.9% | 4.3% | 4.9% | 4.0% | 4.9% | 7.6% | 5.1% | 6.4% | 5.8% | 4.3% | 3.1% | 6.2% | 3.5% | 5.0% | 4.0% | 5.0% | 5.5% | 3.0% | 6.2% | 3.3% | 5.4% | 5.0% | 7.0% | 6.6% | 2.8% | 6.1% | 4.5% | 3.1% | 4.4% | 4.0% | 5.0% | 4.4% | 4.4% | 2.7% |
| 2008-06-01 | 5.6% | 5.6% | 6.5% | 5.5% | 5.1% | 7.0% | 4.7% | 5.5% | 4.7% | 6.6% | 5.5% | 6.4% | 3.8% | 5.1% | 6.4% | 5.5% | 4.0% | 4.4% | 6.1% | 4.4% | 5.1% | 4.2% | 5.1% | 7.9% | 5.3% | 6.6% | 6.0% | 4.5% | 3.2% | 6.5% | 3.6% | 5.2% | 4.1% | 5.2% | 5.7% | 3.1% | 6.4% | 3.4% | 5.7% | 5.1% | 7.3% | 6.9% | 2.9% | 6.4% | 4.7% | 3.2% | 4.5% | 4.1% | 5.2% | 4.4% | 4.6% | 2.8% |
| 2008-07-01 | 5.8% | 5.9% | 6.5% | 5.9% | 5.3% | 7.3% | 4.8% | 5.7% | 5.0% | 6.8% | 5.8% | 6.6% | 4.0% | 5.4% | 6.6% | 5.8% | 4.1% | 4.5% | 6.4% | 4.6% | 5.3% | 4.5% | 5.3% | 8.1% | 5.4% | 6.8% | 6.2% | 4.7% | 3.2% | 6.8% | 3.7% | 5.4% | 4.2% | 5.3% | 5.8% | 3.1% | 6.7% | 3.5% | 6.0% | 5.2% | 7.7% | 7.3% | 3.1% | 6.6% | 4.8% | 3.2% | 4.6% | 4.3% | 5.3% | 4.5% | 4.7% | 2.9% |
| 2008-08-01 | 6.1% | 6.1% | 6.5% | 6.2% | 5.4% | 7.6% | 5.0% | 5.9% | 5.3% | 7.0% | 6.1% | 6.9% | 4.3% | 5.6% | 6.7% | 6.0% | 4.2% | 4.7% | 6.7% | 4.8% | 5.5% | 4.7% | 5.5% | 8.4% | 5.6% | 6.9% | 6.4% | 4.9% | 3.3% | 7.2% | 3.8% | 5.6% | 4.4% | 5.5% | 6.0% | 3.2% | 6.9% | 3.6% | 6.4% | 5.4% | 8.0% | 7.6% | 3.2% | 6.8% | 5.0% | 3.3% | 4.7% | 4.4% | 5.4% | 4.5% | 4.9% | 3.0% |
| 2008-09-01 | 6.1% | 6.5% | 6.6% | 6.6% | 5.6% | 8.0% | 5.2% | 6.0% | 5.6% | 7.2% | 6.4% | 7.4% | 4.5% | 5.9% | 6.9% | 6.4% | 4.4% | 4.8% | 7.1% | 5.0% | 5.7% | 5.0% | 5.7% | 8.7% | 5.7% | 7.0% | 6.6% | 5.1% | 3.4% | 7.6% | 3.9% | 5.9% | 4.5% | 5.7% | 6.1% | 3.2% | 7.1% | 3.7% | 6.9% | 5.5% | 8.4% | 8.0% | 3.4% | 7.0% | 5.2% | 3.4% | 4.8% | 4.5% | 5.6% | 4.7% | 5.2% | 3.1% |
| 2008-10-01 | 6.5% | 6.9% | 6.6% | 6.9% | 5.9% | 8.4% | 5.4% | 6.3% | 6.0% | 7.5% | 6.7% | 7.9% | 4.8% | 6.3% | 7.1% | 6.9% | 4.6% | 5.0% | 7.5% | 5.2% | 6.1% | 5.3% | 6.0% | 9.1% | 6.0% | 7.2% | 6.9% | 5.4% | 3.5% | 8.1% | 4.1% | 6.2% | 4.7% | 6.0% | 6.3% | 3.3% | 7.3% | 3.9% | 7.4% | 5.8% | 8.7% | 8.4% | 3.5% | 7.3% | 5.4% | 3.5% | 4.9% | 4.7% | 5.8% | 5.0% | 5.6% | 3.2% |
| 2008-11-01 | 6.8% | 7.3% | 6.7% | 7.3% | 6.3% | 8.8% | 5.7% | 6.5% | 6.3% | 7.9% | 7.1% | 8.3% | 5.1% | 6.7% | 7.4% | 7.5% | 4.9% | 5.2% | 8.1% | 5.5% | 6.5% | 5.7% | 6.3% | 9.6% | 6.3% | 7.4% | 7.2% | 5.8% | 3.7% | 8.6% | 4.3% | 6.5% | 5.0% | 6.3% | 8.6% | 3.4% | 7.7% | 4.2% | 8.1% | 6.2% | 9.2% | 8.9% | 3.7% | 7.7% | 5.6% | 3.6% | 5.1% | 5.0% | 6.1% | 5.4% | 6.1% | 3.4% |
| 2008-12-01 | 7.3% | 7.8% | 6.9% | 7.7% | 6.7% | 9.3% | 6.1% | 6.8% | 6.8% | 8.2% | 7.4% | 8.8% | 5.5% | 7.2% | 7.9% | 8.3% | 5.2% | 5.5% | 8.7% | 5.7% | 7.0% | 6.2% | 6.7% | 10.1% | 6.7% | 7.7% | 7.6% | 6.2% | 3.9% | 9.2% | 4.6% | 6.9% | 5.4% | 6.7% | 9.6% | 3.6% | 8.1% | 4.7% | 8.9% | 6.6% | 9.7% | 9.4% | 3.9% | 8.2% | 5.9% | 5.2% | 5.3% | 5.4% | 6.4% | 5.9% | 6.7% | 3.7% |
| 2009-01-01 | 7.8% | 8.4% | 7.2% | 8.2% | 7.0% | 9.9% | 6.6% | 7.1% | 7.2% | 8.7% | 7.8% | 9.2% | 5.9% | 7.6% | 8.4% | 9.0% | 5.6% | 5.8% | 9.4% | 6.0% | 7.5% | 6.6% | 7.0% | 10.9% | 7.2% | 8.1% | 8.0% | 6.6% | 4.1% | 9.7% | 5.0% | 7.3% | 5.8% | 7.1% | 10.2% | 3.8% | 8.6% | 5.2% | 9.7% | 7.0% | 10.2% | 10.0% | 4.1% | 8.7% | 6.1% | 6.1% | 5.5% | 5.7% | 6.8% | 6.5% | 7.4% | 4.2% |
| 2009-02-01 | 8.3% | 8.8% | 7.4% | 8.6% | 7.4% | 10.4% | 7.0% | 7.4% | 7.6% | 9.0% | 8.2% | 9.6% | 6.2% | 7.9% | 8.9% | 9.8% | 6.0% | 6.1% | 10.0% | 6.2% | 7.9% | 7.0% | 7.4% | 11.8% | 7.6% | 8.5% | 8.3% | 6.9% | 4.3% | 10.2% | 5.3% | 7.8% | 6.2% | 7.5% | 10.8% | 3.9% | 9.1% | 5.7% | 10.5% | 7.4% | 10.7% | 10.5% | 4.4% | 9.2% | 6.3% | 6.5% | 5.7% | 6.1% | 7.2% | 7.1% | 8.1% | 4.8% |
| 2009-03-01 | 8.7% | 9.3% | 7.7% | 8.9% | 7.6% | 10.8% | 7.4% | 7.7% | 7.9% | 9.4% | 8.5% | 10.0% | 6.5% | 8.2% | 9.4% | 10.3% | 6.3% | 6.5% | 10.6% | 6.5% | 8.3% | 7.3% | 7.7% | 12.5% | 7.9% | 8.8% | 8.6% | 7.1% | 4.5% | 10.7% | 5.7% | 8.1% | 6.6% | 7.9% | 11.2% | 4.0% | 9.5% | 6.1% | 11.0% | 7.7% | 11.2% | 10.9% | 4.5% | 9.7% | 6.4% | 6.8% | 5.9% | 6.4% | 7.5% | 7.7% | 8.6% | 5.4% |
| 2009-04-01 | 9.0% | 9.6% | 7.9% | 9.2% | 7.8% | 11.2% | 7.7% | 7.9% | 8.2% | 9.7% | 8.8% | 10.2% | 6.6% | 8.2% | 9.8% | 10.7% | 6.5% | 6.8% | 10.9% | 6.8% | 8.5% | 7.5% | 7.9% | 13.1% | 8.1% | 9.0% | 8.9% | 7.2% | 4.6% | 11.1% | 5.9% | 8.5% | 6.9% | 8.1% | 11.4% | 4.0% | 9.9% | 6.5% | 11.3% | 8.0% | 11.4% | 11.2% | 4.7% | 10.1% | 6.5% | 7.0% | 6.1% | 6.6% | 7.8% | 8.1% | 9.0% | 5.9% |
| 2009-05-01 | 9.4% | 9.9% | 8.0% | 9.5% | 7.9% | 11.4% | 8.0% | 8.1% | 8.3% | 9.9% | 9.4% | 10.4% | 6.7% | 8.9% | 10.0% | 10.8% | 6.6% | 7.0% | 11.1% | 6.9% | 8.5% | 7.6% | 8.1% | 13.6% | 8.2% | 9.2% | 9.0% | 7.2% | 4.7% | 11.4% | 6.1% | 8.7% | 7.1% | 8.3% | 11.4% | 4.0% | 10.1% | 6.7% | 11.3% | 8.1% | 11.6% | 11.4% | 4.7% | 10.3% | 7.5% | 7.1% | 6.1% | 6.8% | 8.1% | 8.5% | 9.3% | 6.3% |
| 2009-06-01 | 9.5% | 10.2% | 8.1% | 9.7% | 7.9% | 11.7% | 8.1% | 8.3% | 8.4% | 10.1% | 9.7% | 10.6% | 6.8% | 9.1% | 10.3% | 10.8% | 6.6% | 7.2% | 11.2% | 7.0% | 8.6% | 7.7% | 8.2% | 14.0% | 8.2% | 9.3% | 9.1% | 7.2% | 4.7% | 11.7% | 6.3% | 9.0% | 7.3% | 8.5% | 11.3% | 3.9% | 10.2% | 6.9% | 11.2% | 8.2% | 11.6% | 11.5% | 4.7% | 10.4% | 8.0% | 7.3% | 6.2% | 6.9% | 8.3% | 8.7% | 9.4% | 6.5% |
| 2009-07-01 | 9.5% | 10.4% | 8.1% | 10.0% | 7.9% | 11.8% | 8.1% | 8.4% | 8.5% | 10.3% | 9.9% | 10.7% | 6.8% | 9.1% | 10.4% | 10.7% | 6.6% | 7.2% | 11.2% | 7.0% | 8.5% | 7.7% | 8.3% | 14.0% | 8.1% | 9.4% | 9.2% | 7.1% | 4.8% | 12.0% | 6.4% | 9.2% | 7.3% | 8.6% | 11.2% | 3.9% | 10.4% | 6.9% | 11.0% | 8.2% | 11.6% | 11.6% | 4.6% | 10.5% | 8.2% | 7.4% | 6.2% | 7.0% | 8.5% | 8.8% | 9.3% | 6.6% |
| 2009-08-01 | 9.6% | 10.6% | 8.2% | 10.1% | 7.8% | 12.0% | 8.1% | 8.6% | 8.6% | 10.5% | 10.1% | 10.8% | 6.8% | 9.1% | 10.6% | 10.7% | 6.6% | 7.3% | 11.1% | 7.0% | 8.5% | 7.7% | 8.4% | 13.8% | 8.0% | 9.6% | 9.3% | 7.1% | 4.8% | 12.3% | 6.5% | 9.4% | 7.4% | 8.7% | 11.0% | 3.9% | 10.5% | 6.9% | 10.8% | 8.2% | 11.6% | 11.8% | 4.6% | 10.5% | 8.3% | 7.6% | 6.3% | 7.1% | 8.7% | 8.8% | 9.3% | 6.7% |
| 2009-09-01 | 9.8% | 10.8% | 8.2% | 10.3% | 7.8% | 12.1% | 8.2% | 8.8% | 8.7% | 10.6% | 10.3% | 10.8% | 6.9% | 9.1% | 10.8% | 10.6% | 6.5% | 7.2% | 11.0% | 7.0% | 8.5% | 7.8% | 8.4% | 13.7% | 8.0% | 9.8% | 9.4% | 7.1% | 4.8% | 12.5% | 6.5% | 9.6% | 7.4% | 8.8% | 10.9% | 3.9% | 10.6% | 6.9% | 10.7% | 8.2% | 11.6% | 11.9% | 4.6% | 10.5% | 8.3% | 7.7% | 6.4% | 7.2% | 9.0% | 8.8% | 9.3% | 6.8% |
| 2009-10-01 | 10.0% | 10.9% | 8.3% | 10.4% | 7.8% | 12.3% | 8.3% | 9.0% | 8.8% | 10.6% | 10.5% | 10.9% | 6.9% | 9.1% | 11.0% | 10.6% | 6.5% | 7.2% | 10.9% | 7.0% | 8.6% | 7.8% | 8.5% | 13.5% | 7.9% | 10.0% | 9.4% | 7.2% | 4.8% | 12.8% | 6.6% | 9.8% | 7.5% | 8.9% | 10.9% | 3.9% | 10.8% | 6.9% | 10.6% | 8.2% | 11.7% | 12.0% | 4.6% | 10.5% | 8.3% | 7.8% | 6.5% | 7.3% | 9.0% | 8.8% | 9.2% | 7.1% |
| 2009-11-01 | 9.9% | 11.0% | 8.3% | 10.5% | 7.9% | 12.4% | 8.4% | 9.2% | 8.9% | 10.6% | 10.7% | 10.9% | 6.9% | 9.1% | 11.2% | 10.6% | 6.5% | 7.2% | 10.9% | 7.0% | 8.6% | 7.9% | 8.5% | 13.4% | 7.9% | 10.2% | 9.5% | 7.3% | 4.9% | 13.0% | 6.7% | 9.9% | 7.5% | 9.0% | 11.0% | 3.9% | 10.9% | 7.0% | 10.7% | 8.2% | 11.7% | 12.0% | 4.7% | 10.5% | 8.3% | 7.9% | 6.5% | 7.4% | 9.1% | 8.9% | 9.3% | 7.3% |
| 2009-12-01 | 9.9% | 11.1% | 8.4% | 10.6% | 7.9% | 12.5% | 8.6% | 9.4% | 9.0% | 10.6% | 10.8% | 10.8% | 6.9% | 9.1% | 11.4% | 10.6% | 6.5% | 7.2% | 10.9% | 7.1% | 8.7% | 8.0% | 8.5% | 13.3% | 7.8% | 10.4% | 9.6% | 7.4% | 4.9% | 13.3% | 6.7% | 9.9% | 7.6% | 9.0% | 11.1% | 3.9% | 11.1% | 7.0% | 10.7% | 8.3% | 11.8% | 12.1% | 4.8% | 10.5% | 8.3% | 7.9% | 6.6% | 7.5% | 9.2% | 8.9% | 9.3% | 7.5% |
| 2010-01-01 | 9.8% | 11.1% | 8.4% | 10.6% | 7.9% | 12.6% | 8.8% | 9.5% | 9.1% | 10.5% | 10.9% | 10.8% | 6.9% | 9.1% | 11.4% | 10.7% | 6.5% | 7.2% | 10.9% | 7.1% | 8.7% | 8.1% | 8.5% | 13.2% | 7.8% | 10.5% | 9.7% | 7.5% | 4.9% | 13.5% | 6.7% | 10.0% | 7.8% | 9.0% | 11.2% | 3.9% | 11.1% | 7.0% | 10.8% | 8.4% | 11.8% | 12.0% | 4.8% | 10.5% | 8.3% | 8.0% | 6.7% | 7.6% | 9.3% | 9.0% | 9.3% | 7.6% |
| 2010-02-01 | 9.8% | 11.0% | 8.4% | 10.6% | 7.9% | 12.6% | 9.0% | 9.6% | 9.0% | 10.3% | 10.9% | 10.8% | 6.9% | 9.1% | 11.3% | 10.7% | 6.4% | 7.2% | 10.8% | 7.2% | 8.7% | 8.1% | 8.4% | 13.1% | 7.7% | 10.5% | 9.7% | 7.5% | 4.9% | 13.6% | 6.6% | 9.9% | 7.8% | 9.0% | 11.2% | 3.9% | 11.1% | 6.9% | 10.9% | 8.5% | 11.9% | 11.8% | 4.9% | 10.4% | 8.3% | 8.0% | 6.6% | 7.6% | 9.3% | 8.9% | 9.2% | 7.6% |
| 2010-03-01 | 9.9% | 10.9% | 8.4% | 10.6% | 7.9% | 12.6% | 9.1% | 9.7% | 9.0% | 10.2% | 10.9% | 10.8% | 6.9% | 9.0% | 11.2% | 10.6% | 6.3% | 7.1% | 10.7% | 7.3% | 8.7% | 8.0% | 8.4% | 12.9% | 7.6% | 10.4% | 9.6% | 7.4% | 4.9% | 13.7% | 6.5% | 9.9% | 7.9% | 8.9% | 11.2% | 3.9% | 10.9% | 6.8% | 10.9% | 8.5% | 11.8% | 11.7% | 4.9% | 10.2% | 8.3% | 8.0% | 6.6% | 7.6% | 9.3% | 8.8% | 9.0% | 7.5% |
| 2010-04-01 | 9.9% | 10.5% | 8.3% | 10.5% | 7.8% | 12.5% | 9.1% | 9.6% | 8.8% | 10.0% | 10.9% | 10.7% | 6.8% | 8.9% | 10.9% | 10.4% | 6.2% | 7.0% | 10.5% | 7.3% | 8.6% | 7.9% | 8.3% | 12.7% | 7.5% | 10.4% | 9.6% | 7.4% | 4.8% | 13.8% | 6.3% | 9.8% | 7.9% | 8.8% | 11.0% | 3.8% | 10.7% | 6.7% | 10.9% | 8.4% | 11.8% | 11.5% | 4.9% | 10.0% | 8.2% | 8.0% | 6.5% | 7.5% | 9.2% | 8.7% | 8.8% | 7.2% |
| 2010-05-01 | 9.6% | 10.3% | 8.2% | 10.4% | 7.8% | 12.5% | 9.0% | 9.6% | 8.7% | 9.8% | 10.8% | 10.6% | 6.8% | 8.8% | 10.7% | 10.3% | 6.1% | 6.9% | 10.3% | 7.4% | 8.5% | 7.9% | 8.1% | 12.5% | 7.4% | 10.3% | 9.5% | 7.2% | 4.7% | 13.7% | 6.1% | 9.7% | 7.9% | 8.8% | 10.8% | 3.7% | 10.4% | 6.6% | 10.8% | 8.3% | 11.7% | 11.3% | 4.9% | 9.8% | 8.2% | 8.0% | 6.4% | 7.4% | 9.1% | 8.5% | 8.6% | 7.0% |
| 2010-06-01 | 9.4% | 10.1% | 8.0% | 10.3% | 7.7% | 12.4% | 9.0% | 9.5% | 8.6% | 9.7% | 10.8% | 10.5% | 6.8% | 8.7% | 10.4% | 10.1% | 6.0% | 6.8% | 10.1% | 7.4% | 8.3% | 7.8% | 8.0% | 12.4% | 7.3% | 9.9% | 9.4% | 7.1% | 4.6% | 13.7% | 6.0% | 9.6% | 7.8% | 8.7% | 10.6% | 3.7% | 10.2% | 6.4% | 10.7% | 8.1% | 11.6% | 11.2% | 4.9% | 9.6% | 8.1% | 7.9% | 6.3% | 7.3% | 9.0% | 8.5% | 8.4% | 6.8% |
| 2010-07-01 | 9.4% | 10.1% | 7.9% | 10.2% | 7.7% | 12.3% | 9.1% | 9.5% | 8.6% | 9.7% | 10.8% | 10.5% | 6.8% | 8.6% | 10.2% | 10.0% | 6.0% | 6.8% | 10.0% | 7.6% | 8.3% | 7.7% | 7.9% | 12.3% | 7.2% | 9.8% | 9.4% | 7.0% | 4.6% | 13.7% | 5.9% | 9.5% | 7.8% | 8.6% | 10.4% | 3.6% | 10.0% | 6.4% | 10.7% | 8.0% | 11.5% | 11.1% | 4.9% | 9.5% | 8.1% | 7.9% | 6.2% | 7.2% | 9.0% | 8.4% | 8.3% | 6.6% |
| 2010-08-01 | 9.5% | 10.0% | 7.9% | 10.2% | 7.8% | 12.4% | 9.2% | 9.5% | 8.5% | 9.7% | 10.8% | 10.6% | 6.8% | 8.6% | 10.1% | 9.9% | 6.0% | 6.8% | 10.0% | 7.7% | 8.3% | 7.7% | 7.9% | 12.0% | 7.3% | 9.8% | 9.4% | 7.0% | 4.6% | 13.7% | 5.8% | 9.5% | 7.8% | 8.6% | 10.4% | 3.6% | 9.9% | 6.3% | 10.6% | 8.0% | 11.5% | 11.1% | 4.9% | 9.5% | 8.1% | 7.9% | 6.1% | 7.2% | 9.1% | 8.5% | 8.2% | 6.6% |
| 2010-09-01 | 9.5% | 10.1% | 8.0% | 10.1% | 7.9% | 12.4% | 9.3% | 9.5% | 8.5% | 9.8% | 10.8% | 10.6% | 6.8% | 8.6% | 10.0% | 9.8% | 6.0% | 6.8% | 10.0% | 7.8% | 8.3% | 7.7% | 7.9% | 11.7% | 7.3% | 9.8% | 9.4% | 7.0% | 4.6% | 13.8% | 5.8% | 9.5% | 7.8% | 8.6% | 10.4% | 3.6% | 9.9% | 6.3% | 10.6% | 8.0% | 11.5% | 11.1% | 4.9% | 9.5% | 8.1% | 7.9% | 6.1% | 7.1% | 9.1% | 8.6% | 8.2% | 6.6% |
| 2010-10-01 | 9.4% | 10.1% | 8.0% | 10.1% | 7.9% | 12.4% | 9.4% | 9.6% | 8.5% | 9.9% | 10.8% | 10.7% | 6.8% | 8.6% | 9.9% | 9.7% | 6.0% | 6.9% | 10.0% | 7.8% | 8.3% | 7.7% | 7.8% | 11.5% | 7.3% | 9.8% | 9.5% | 7.0% | 4.6% | 13.9% | 5.8% | 9.5% | 7.7% | 8.6% | 10.4% | 3.6% | 9.8% | 6.3% | 10.6% | 8.0% | 11.5% | 11.0% | 4.9% | 9.6% | 8.2% | 7.9% | 6.1% | 7.1% | 9.1% | 8.6% | 8.1% | 6.6% |
| 2010-11-01 | 9.8% | 10.2% | 8.1% | 10.0% | 8.0% | 12.4% | 9.4% | 9.6% | 8.4% | 9.9% | 10.8% | 10.7% | 6.8% | 8.6% | 9.8% | 9.5% | 6.0% | 6.9% | 10.0% | 7.8% | 8.2% | 7.7% | 7.8% | 11.2% | 7.2% | 9.9% | 9.5% | 7.1% | 4.6% | 13.9% | 5.8% | 9.5% | 7.6% | 8.5% | 10.5% | 3.5% | 9.7% | 6.2% | 10.5% | 7.9% | 11.5% | 10.9% | 5.0% | 9.7% | 8.2% | 7.9% | 6.1% | 7.0% | 9.1% | 8.6% | 8.0% | 6.6% |
| 2010-12-01 | 9.3% | 10.1% | 8.0% | 10.0% | 8.0% | 12.4% | 9.3% | 9.5% | 8.2% | 9.9% | 10.7% | 10.6% | 6.8% | 8.5% | 9.7% | 9.3% | 5.9% | 6.8% | 9.9% | 7.8% | 8.1% | 7.6% | 7.7% | 10.8% | 7.1% | 9.9% | 9.4% | 7.0% | 4.6% | 13.8% | 5.7% | 9.5% | 7.5% | 8.5% | 10.5% | 3.5% | 9.5% | 6.1% | 10.3% | 7.9% | 11.4% | 10.9% | 5.0% | 9.6% | 8.2% | 7.8% | 6.1% | 6.9% | 9.0% | 8.5% | 7.9% | 6.6% |
| 2011-01-01 | 9.1% | 10.1% | 8.0% | 9.8% | 8.0% | 12.3% | 9.1% | 9.4% | 8.1% | 10.0% | 10.6% | 10.5% | 6.8% | 8.5% | 9.6% | 9.1% | 5.9% | 6.8% | 9.8% | 7.8% | 8.1% | 7.5% | 7.6% | 10.5% | 6.9% | 9.9% | 9.3% | 7.0% | 4.6% | 13.7% | 5.6% | 9.5% | 7.4% | 8.4% | 10.4% | 3.5% | 9.3% | 5.9% | 10.1% | 7.8% | 11.2% | 10.8% | 5.0% | 9.6% | 8.2% | 7.8% | 6.0% | 6.7% | 8.9% | 8.4% | 7.8% | 6.6% |
| 2011-02-01 | 9.0% | 10.0% | 7.9% | 9.8% | 8.0% | 12.2% | 8.9% | 9.4% | 7.9% | 10.0% | 10.5% | 10.4% | 6.7% | 8.4% | 9.5% | 8.9% | 5.8% | 6.7% | 9.6% | 7.7% | 8.0% | 7.4% | 7.5% | 10.4% | 6.8% | 9.8% | 9.2% | 6.9% | 4.6% | 13.6% | 5.5% | 9.4% | 7.2% | 8.3% | 10.3% | 3.4% | 9.1% | 5.8% | 9.8% | 7.7% | 11.1% | 10.7% | 4.9% | 9.5% | 8.2% | 7.7% | 5.9% | 6.6% | 8.8% | 8.3% | 7.7% | 6.5% |
| 2011-03-01 | 9.0% | 9.9% | 7.8% | 9.7% | 8.0% | 12.1% | 8.8% | 9.3% | 7.8% | 10.1% | 10.4% | 10.3% | 6.7% | 8.4% | 9.5% | 8.8% | 5.7% | 6.6% | 9.5% | 7.6% | 7.9% | 7.4% | 7.4% | 9.9% | 6.7% | 9.8% | 9.0% | 6.8% | 4.5% | 13.5% | 5.4% | 9.4% | 7.1% | 8.2% | 10.2% | 3.4% | 9.0% | 5.6% | 9.7% | 7.6% | 11.0% | 10.7% | 4.9% | 9.4% | 8.1% | 7.7% | 5.9% | 6.6% | 8.8% | 8.1% | 7.6% | 6.3% |
| 2011-04-01 | 9.1% | 9.9% | 7.8% | 9.6% | 8.0% | 12.0% | 8.7% | 9.2% | 7.7% | 10.3% | 10.3% | 10.3% | 6.7% | 8.4% | 9.6% | 8.7% | 5.7% | 6.5% | 9.5% | 7.5% | 7.8% | 7.3% | 7.4% | 10.0% | 6.7% | 9.9% | 8.9% | 6.8% | 4.5% | 13.5% | 5.4% | 9.4% | 7.1% | 8.2% | 10.2% | 3.4% | 9.0% | 5.6% | 9.6% | 7.6% | 11.0% | 10.7% | 4.8% | 9.3% | 8.1% | 7.7% | 5.8% | 6.5% | 8.7% | 8.0% | 7.6% | 6.2% |
| 2011-05-01 | 9.0% | 9.8% | 7.7% | 9.6% | 8.0% | 12.0% | 8.7% | 9.2% | 7.7% | 10.4% | 10.2% | 10.3% | 6.8% | 8.3% | 9.8% | 8.8% | 5.7% | 6.4% | 9.5% | 7.4% | 7.8% | 7.4% | 7.3% | 10.1% | 6.7% | 9.9% | 8.8% | 6.7% | 4.5% | 13.4% | 5.5% | 9.4% | 7.1% | 8.2% | 10.2% | 3.4% | 9.0% | 5.5% | 9.6% | 7.7% | 11.0% | 10.7% | 4.7% | 9.3% | 8.2% | 7.7% | 5.7% | 6.5% | 8.6% | 7.9% | 7.6% | 6.1% |
| 2011-06-01 | 9.1% | 9.8% | 7.7% | 9.6% | 8.0% | 12.0% | 8.7% | 9.1% | 7.7% | 10.5% | 10.1% | 10.3% | 6.9% | 8.3% | 9.9% | 8.9% | 5.7% | 6.4% | 9.5% | 7.4% | 7.8% | 7.4% | 7.3% | 10.2% | 6.7% | 9.9% | 8.8% | 6.7% | 4.4% | 13.5% | 5.5% | 9.4% | 7.1% | 8.3% | 10.3% | 3.4% | 9.0% | 5.5% | 9.7% | 7.8% | 11.0% | 10.7% | 4.6% | 9.2% | 8.3% | 7.7% | 5.7% | 6.6% | 8.6% | 7.8% | 7.6% | 6.0% |
| 2011-07-01 | 9.0% | 9.7% | 7.7% | 9.5% | 8.0% | 12.0% | 8.7% | 9.0% | 7.6% | 10.5% | 10.0% | 10.2% | 7.0% | 8.2% | 10.0% | 9.1% | 5.7% | 6.3% | 9.5% | 7.4% | 7.8% | 7.4% | 7.2% | 10.2% | 6.7% | 9.9% | 8.7% | 6.7% | 4.4% | 13.4% | 5.5% | 9.4% | 7.2% | 8.3% | 10.3% | 3.4% | 9.0% | 5.6% | 9.7% | 7.8% | 11.0% | 10.6% | 4.5% | 9.2% | 8.3% | 7.4% | 5.6% | 6.6% | 8.6% | 7.8% | 7.6% | 6.0% |
| 2011-08-01 | 9.0% | 9.6% | 7.7% | 9.4% | 8.0% | 11.9% | 8.6% | 9.0% | 7.6% | 10.4% | 9.9% | 10.2% | 7.0% | 8.1% | 10.1% | 9.1% | 5.7% | 6.3% | 9.4% | 7.3% | 7.7% | 7.4% | 7.2% | 10.1% | 6.6% | 9.9% | 8.6% | 6.6% | 4.4% | 13.4% | 5.5% | 9.4% | 7.3% | 8.4% | 10.4% | 3.4% | 8.9% | 5.6% | 9.6% | 7.9% | 11.0% | 10.5% | 4.5% | 9.1% | 8.2% | 7.0% | 5.5% | 6.6% | 8.5% | 7.8% | 7.6% | 6.0% |
| 2011-09-01 | 9.0% | 9.4% | 7.7% | 9.3% | 7.9% | 11.8% | 8.6% | 8.8% | 7.5% | 10.3% | 9.7% | 10.1% | 7.0% | 8.0% | 10.0% | 9.1% | 5.6% | 6.3% | 9.3% | 7.3% | 7.6% | 7.3% | 7.1% | 9.9% | 6.4% | 9.8% | 8.4% | 6.5% | 4.3% | 13.3% | 5.5% | 9.3% | 7.3% | 8.4% | 10.3% | 3.4% | 8.7% | 5.6% | 9.6% | 7.9% | 11.0% | 10.3% | 4.4% | 8.9% | 8.0% | 6.6% | 5.4% | 6.6% | 8.4% | 7.7% | 7.5% | 6.0% |
| 2011-10-01 | 8.8% | 9.2% | 7.7% | 9.1% | 7.8% | 11.6% | 8.6% | 8.7% | 7.4% | 10.1% | 9.6% | 9.9% | 6.9% | 7.9% | 9.9% | 9.0% | 5.5% | 6.2% | 9.2% | 7.3% | 7.5% | 7.2% | 7.0% | 9.8% | 6.2% | 9.7% | 8.2% | 6.4% | 4.3% | 13.1% | 5.4% | 9.3% | 7.3% | 8.5% | 10.2% | 3.3% | 8.5% | 5.5% | 9.4% | 7.8% | 11.0% | 10.1% | 4.4% | 8.8% | 7.8% | 6.2% | 5.2% | 6.5% | 8.3% | 7.5% | 7.4% | 6.0% |
| 2011-11-01 | 8.6% | 8.9% | 7.6% | 9.0% | 7.7% | 11.5% | 8.5% | 8.6% | 7.2% | 9.9% | 9.4% | 9.8% | 6.8% | 7.8% | 9.7% | 8.8% | 5.5% | 6.1% | 9.0% | 7.3% | 7.4% | 7.1% | 6.9% | 9.6% | 6.0% | 9.5% | 8.0% | 6.3% | 4.2% | 12.8% | 5.3% | 9.3% | 7.3% | 8.5% | 10.1% | 3.2% | 8.3% | 5.5% | 9.3% | 7.7% | 11.0% | 9.9% | 4.3% | 8.6% | 7.5% | 5.8% | 5.1% | 6.4% | 8.1% | 7.4% | 7.3% | 6.0% |
| 2011-12-01 | 8.5% | 8.7% | 7.5% | 8.8% | 7.5% | 11.3% | 8.4% | 8.5% | 7.1% | 9.8% | 9.3% | 9.6% | 6.7% | 7.7% | 9.5% | 8.6% | 5.3% | 6.0% | 8.7% | 7.2% | 7.3% | 7.0% | 6.8% | 9.4% | 5.9% | 9.3% | 7.8% | 6.1% | 4.1% | 12.6% | 5.3% | 9.3% | 7.2% | 8.6% | 9.9% | 3.1% | 8.0% | 5.4% | 9.2% | 7.6% | 10.9% | 9.7% | 4.2% | 8.4% | 7.3% | 5.4% | 5.0% | 6.3% | 8.0% | 7.2% | 7.1% | 5.9% |
| 2012-01-01 | 8.3% | 8.5% | 7.5% | 8.7% | 7.4% | 11.2% | 8.4% | 8.4% | 7.0% | 9.6% | 9.2% | 9.5% | 6.6% | 7.7% | 9.3% | 8.4% | 5.2% | 5.9% | 8.5% | 7.1% | 7.2% | 6.9% | 6.7% | 9.2% | 5.8% | 9.1% | 7.6% | 6.0% | 4.1% | 12.3% | 5.2% | 9.3% | 7.1% | 8.6% | 9.7% | 3.0% | 7.8% | 5.3% | 9.1% | 7.5% | 10.7% | 9.6% | 4.2% | 8.2% | 7.1% | 5.3% | 4.9% | 6.2% | 8.0% | 7.1% | 7.0% | 5.8% |
| 2012-02-01 | 8.3% | 8.4% | 7.4% | 8.6% | 7.3% | 11.0% | 8.3% | 8.3% | 7.0% | 9.5% | 9.1% | 9.4% | 6.5% | 7.6% | 9.1% | 8.3% | 5.2% | 5.9% | 8.4% | 7.1% | 7.2% | 6.9% | 6.7% | 9.1% | 5.7% | 9.0% | 7.5% | 5.9% | 4.0% | 12.2% | 5.2% | 9.3% | 7.0% | 8.6% | 9.6% | 2.9% | 7.7% | 5.1% | 9.0% | 7.5% | 10.6% | 9.5% | 4.1% | 8.1% | 7.0% | 4.7% | 4.9% | 6.2% | 7.9% | 7.0% | 6.9% | 5.7% |
| 2012-03-01 | 8.2% | 8.4% | 7.4% | 8.6% | 7.3% | 11.0% | 8.3% | 8.3% | 7.0% | 9.3% | 9.0% | 9.3% | 6.4% | 7.6% | 9.0% | 8.2% | 5.1% | 5.8% | 8.2% | 7.0% | 7.2% | 6.9% | 6.7% | 9.1% | 5.7% | 8.9% | 7.4% | 5.9% | 3.9% | 12.1% | 5.3% | 9.4% | 7.0% | 8.7% | 9.5% | 2.9% | 7.6% | 5.1% | 9.0% | 7.5% | 10.5% | 9.4% | 4.1% | 8.0% | 6.7% | 4.8% | 4.8% | 6.1% | 7.9% | 7.1% | 6.9% | 5.6% |
| 2012-04-01 | 8.2% | 8.4% | 7.3% | 8.5% | 7.3% | 10.9% | 8.3% | 8.4% | 7.0% | 9.2% | 8.9% | 9.3% | 6.3% | 7.6% | 9.0% | 8.2% | 5.1% | 5.8% | 8.2% | 7.0% | 7.2% | 6.9% | 6.7% | 9.1% | 5.7% | 8.9% | 7.3% | 5.9% | 3.9% | 12.0% | 5.4% | 9.5% | 7.0% | 8.8% | 9.5% | 2.9% | 7.5% | 5.1% | 8.9% | 7.6% | 10.5% | 9.4% | 4.1% | 8.0% | 6.8% | 4.8% | 4.9% | 6.1% | 7.9% | 7.2% | 7.0% | 5.6% |
| 2012-05-01 | 8.2% | 8.4% | 7.3% | 8.5% | 7.3% | 10.8% | 8.2% | 8.4% | 7.1% | 9.1% | 8.9% | 9.2% | 6.2% | 7.5% | 9.0% | 8.2% | 5.1% | 5.8% | 8.2% | 6.9% | 7.3% | 6.9% | 6.7% | 9.1% | 5.7% | 8.9% | 7.2% | 5.9% | 3.9% | 11.9% | 5.4% | 9.5% | 7.0% | 8.8% | 9.5% | 2.9% | 7.4% | 5.1% | 8.9% | 7.7% | 10.4% | 9.3% | 4.1% | 8.0% | 6.8% | 4.9% | 4.9% | 6.1% | 8.0% | 7.3% | 7.0% | 5.6% |
| 2012-06-01 | 8.2% | 8.3% | 7.3% | 8.4% | 7.3% | 10.7% | 8.2% | 8.4% | 7.1% | 9.0% | 8.8% | 9.1% | 6.1% | 7.5% | 9.1% | 8.2% | 5.1% | 5.7% | 8.2% | 6.8% | 7.3% | 6.9% | 6.7% | 9.1% | 5.7% | 8.9% | 7.2% | 5.9% | 3.9% | 11.8% | 5.5% | 9.5% | 6.9% | 8.8% | 9.5% | 2.9% | 7.3% | 5.1% | 8.9% | 7.7% | 10.4% | 9.2% | 4.1% | 8.0% | 6.8% | 4.8% | 4.9% | 6.0% | 8.0% | 7.4% | 7.0% | 5.6% |
| 2012-07-01 | 8.2% | 8.2% | 7.2% | 8.3% | 7.3% | 10.5% | 8.1% | 8.4% | 7.1% | 8.8% | 8.6% | 9.0% | 5.9% | 7.4% | 9.0% | 8.2% | 5.1% | 5.7% | 8.2% | 6.7% | 7.2% | 6.9% | 6.7% | 9.0% | 5.7% | 8.8% | 7.1% | 5.9% | 3.9% | 11.6% | 5.6% | 9.5% | 6.9% | 8.7% | 9.5% | 2.9% | 7.3% | 5.1% | 8.8% | 7.8% | 10.3% | 9.0% | 4.1% | 8.0% | 6.7% | 4.8% | 4.9% | 5.9% | 7.8% | 7.4% | 7.0% | 5.5% |
| 2012-08-01 | 8.1% | 8.1% | 7.2% | 8.2% | 7.2% | 10.3% | 7.9% | 8.4% | 7.1% | 8.7% | 8.5% | 8.9% | 5.7% | 7.3% | 9.0% | 8.2% | 5.0% | 5.6% | 8.2% | 6.6% | 7.2% | 6.9% | 6.7% | 9.0% | 5.7% | 8.8% | 7.0% | 5.8% | 3.8% | 11.4% | 5.6% | 9.4% | 6.9% | 8.6% | 9.5% | 2.9% | 7.2% | 5.1% | 8.7% | 7.8% | 10.1% | 8.8% | 4.1% | 7.9% | 6.6% | 4.7% | 4.8% | 5.9% | 7.6% | 7.4% | 6.9% | 5.5% |
| 2012-09-01 | 7.8% | 7.9% | 7.1% | 8.1% | 7.2% | 10.2% | 7.8% | 8.4% | 7.1% | 8.6% | 8.4% | 8.8% | 5.5% | 7.2% | 9.0% | 8.2% | 5.0% | 5.6% | 8.1% | 6.5% | 7.2% | 6.8% | 6.7% | 9.0% | 5.6% | 8.7% | 7.0% | 5.7% | 3.8% | 11.2% | 5.6% | 9.4% | 6.9% | 8.6% | 9.5% | 2.9% | 7.2% | 5.1% | 8.7% | 7.7% | 10.0% | 8.7% | 4.0% | 7.8% | 6.5% | 4.7% | 4.8% | 5.8% | 7.4% | 7.4% | 6.9% | 5.4% |
| 2012-10-01 | 7.8% | 7.8% | 7.1% | 8.1% | 7.2% | 10.0% | 7.6% | 8.3% | 7.1% | 8.6% | 8.3% | 8.7% | 5.3% | 7.2% | 9.0% | 8.2% | 5.0% | 5.6% | 8.1% | 6.4% | 7.1% | 6.8% | 6.7% | 9.0% | 5.6% | 8.7% | 7.0% | 5.6% | 3.8% | 11.1% | 5.6% | 9.3% | 6.9% | 8.5% | 9.5% | 3.0% | 7.2% | 5.1% | 8.6% | 7.7% | 9.8% | 8.6% | 4.0% | 7.8% | 6.5% | 4.6% | 4.7% | 5.7% | 7.2% | 7.3% | 6.8% | 5.3% |
| 2012-11-01 | 7.7% | 7.8% | 7.1% | 8.1% | 7.2% | 9.9% | 7.5% | 8.3% | 7.1% | 8.6% | 8.2% | 8.7% | 5.2% | 7.1% | 9.0% | 8.2% | 4.9% | 5.6% | 8.1% | 6.5% | 7.1% | 6.8% | 6.7% | 9.0% | 5.5% | 8.6% | 7.0% | 5.6% | 3.8% | 10.9% | 5.6% | 9.3% | 7.0% | 8.4% | 9.5% | 3.0% | 7.3% | 5.1% | 8.6% | 7.7% | 9.7% | 8.5% | 3.9% | 7.8% | 6.5% | 4.6% | 4.7% | 5.7% | 7.1% | 7.3% | 6.8% | 5.2% |
| 2012-12-01 | 7.9% | 7.7% | 7.1% | 8.1% | 7.2% | 9.8% | 7.4% | 8.3% | 7.1% | 8.7% | 8.1% | 8.6% | 5.1% | 7.1% | 9.1% | 8.2% | 4.9% | 5.6% | 8.0% | 6.6% | 7.1% | 6.8% | 6.7% | 9.0% | 5.4% | 8.6% | 7.0% | 5.5% | 3.8% | 10.8% | 5.6% | 9.2% | 7.0% | 8.4% | 9.4% | 3.0% | 7.4% | 5.1% | 8.5% | 7.7% | 9.6% | 8.4% | 3.9% | 7.9% | 6.5% | 4.6% | 4.6% | 5.7% | 6.9% | 7.2% | 6.9% | 5.2% |
| 2013-01-01 | 8.0% | 7.6% | 7.1% | 8.1% | 7.2% | 9.7% | 7.3% | 8.3% | 7.1% | 8.7% | 8.0% | 8.6% | 5.0% | 7.0% | 9.2% | 8.2% | 4.9% | 5.6% | 8.0% | 6.7% | 7.1% | 6.8% | 6.7% | 9.0% | 5.4% | 8.7% | 6.9% | 5.5% | 3.8% | 10.7% | 5.6% | 9.1% | 7.0% | 8.3% | 9.4% | 3.0% | 7.5% | 5.2% | 8.4% | 7.6% | 9.6% | 8.4% | 3.9% | 8.0% | 6.5% | 4.5% | 4.6% | 5.6% | 6.9% | 7.1% | 6.9% | 5.1% |
| 2013-02-01 | 7.7% | 7.6% | 7.0% | 8.1% | 7.2% | 9.5% | 7.2% | 8.3% | 7.0% | 8.7% | 8.0% | 8.6% | 4.9% | 7.0% | 9.3% | 8.2% | 4.9% | 5.5% | 8.0% | 6.8% | 7.0% | 6.8% | 6.8% | 9.0% | 5.3% | 8.7% | 6.9% | 5.5% | 3.8% | 10.6% | 5.5% | 9.0% | 7.0% | 8.2% | 9.1% | 3.0% | 7.6% | 5.2% | 8.3% | 7.5% | 9.5% | 8.3% | 3.8% | 8.0% | 6.6% | 4.4% | 4.6% | 5.6% | 6.7% | 6.9% | 6.9% | 5.0% |
| 2013-03-01 | 7.5% | 7.5% | 7.0% | 8.0% | 7.2% | 9.4% | 7.1% | 8.2% | 7.0% | 8.7% | 7.9% | 8.5% | 4.9% | 7.0% | 9.3% | 8.1% | 4.9% | 5.5% | 8.0% | 6.8% | 7.0% | 6.7% | 6.8% | 8.9% | 5.2% | 8.7% | 6.9% | 5.5% | 3.8% | 10.5% | 5.5% | 8.9% | 6.9% | 8.1% | 8.8% | 3.0% | 7.6% | 5.2% | 8.2% | 7.4% | 9.5% | 8.1% | 3.8% | 8.0% | 6.5% | 4.4% | 4.6% | 5.6% | 6.7% | 6.8% | 6.9% | 4.9% |
| 2013-04-01 | 7.6% | 7.4% | 7.0% | 8.0% | 7.2% | 9.3% | 7.0% | 8.2% | 6.9% | 8.6% | 7.8% | 8.4% | 4.8% | 7.0% | 9.3% | 8.0% | 4.9% | 5.4% | 8.0% | 6.7% | 6.9% | 6.7% | 6.8% | 8.9% | 5.2% | 8.7% | 6.9% | 5.5% | 3.8% | 10.4% | 5.4% | 8.8% | 6.9% | 8.0% | 8.5% | 2.9% | 7.6% | 5.2% | 8.0% | 7.3% | 9.5% | 7.9% | 3.8% | 8.0% | 6.5% | 4.3% | 4.5% | 5.6% | 6.7% | 6.7% | 6.9% | 4.8% |
| 2013-05-01 | 7.5% | 7.3% | 7.0% | 7.9% | 7.2% | 9.2% | 6.9% | 8.1% | 6.8% | 8.5% | 7.6% | 8.3% | 4.7% | 7.0% | 9.2% | 7.8% | 4.8% | 5.4% | 8.0% | 6.7% | 6.8% | 6.6% | 6.7% | 8.8% | 5.1% | 8.6% | 6.8% | 5.4% | 3.7% | 10.2% | 5.3% | 8.7% | 6.9% | 7.9% | 8.2% | 2.9% | 7.6% | 5.1% | 7.9% | 7.2% | 9.5% | 7.7% | 3.8% | 7.9% | 6.4% | 4.3% | 4.5% | 5.6% | 6.7% | 6.6% | 6.8% | 4.7% |
| 2013-06-01 | 7.5% | 7.3% | 7.0% | 7.9% | 7.1% | 9.1% | 6.8% | 8.1% | 6.7% | 8.5% | 7.6% | 8.2% | 4.7% | 6.9% | 9.2% | 7.7% | 4.8% | 5.4% | 8.0% | 6.6% | 6.7% | 6.6% | 6.7% | 8.8% | 5.1% | 8.5% | 6.8% | 5.4% | 3.7% | 10.1% | 5.2% | 8.5% | 6.9% | 7.9% | 7.8% | 2.9% | 7.6% | 5.1% | 7.8% | 7.1% | 9.6% | 7.5% | 3.7% | 7.9% | 6.4% | 4.2% | 4.5% | 5.6% | 6.7% | 6.6% | 6.7% | 4.7% |
| 2013-07-01 | 7.3% | 7.2% | 7.0% | 7.8% | 7.1% | 9.0% | 6.8% | 8.0% | 6.6% | 8.5% | 7.5% | 8.1% | 4.7% | 6.9% | 9.2% | 7.5% | 4.7% | 5.3% | 8.0% | 6.5% | 6.7% | 6.5% | 6.7% | 8.8% | 5.0% | 8.5% | 6.8% | 5.4% | 3.7% | 9.9% | 5.2% | 8.4% | 6.9% | 7.8% | 7.5% | 2.9% | 7.6% | 5.1% | 7.7% | 7.1% | 9.6% | 7.4% | 3.7% | 7.8% | 6.3% | 4.2% | 4.4% | 5.6% | 6.7% | 6.6% | 6.7% | 4.6% |
| 2013-08-01 | 7.2% | 7.2% | 7.0% | 7.8% | 7.1% | 8.9% | 6.7% | 7.9% | 6.5% | 8.4% | 7.4% | 8.0% | 4.7% | 6.9% | 9.1% | 7.3% | 4.7% | 5.3% | 8.0% | 6.4% | 6.6% | 6.5% | 6.7% | 8.8% | 5.0% | 8.5% | 6.8% | 5.3% | 3.7% | 9.8% | 5.2% | 8.2% | 6.9% | 7.8% | 7.3% | 2.9% | 7.6% | 5.1% | 7.6% | 7.0% | 9.6% | 7.2% | 3.7% | 7.7% | 6.3% | 4.2% | 4.4% | 5.6% | 6.7% | 6.6% | 6.6% | 4.6% |
| 2013-09-01 | 7.2% | 7.2% | 7.0% | 7.7% | 7.0% | 8.8% | 6.5% | 7.8% | 6.3% | 8.3% | 7.3% | 7.9% | 4.7% | 6.9% | 9.0% | 7.1% | 4.6% | 5.2% | 7.9% | 6.2% | 6.5% | 6.4% | 6.6% | 8.6% | 4.9% | 8.4% | 6.7% | 5.3% | 3.6% | 9.6% | 5.1% | 8.0% | 6.9% | 7.6% | 6.7% | 2.8% | 7.5% | 5.1% | 7.4% | 6.9% | 9.5% | 7.0% | 3.6% | 7.6% | 6.2% | 4.1% | 4.3% | 5.5% | 6.6% | 6.6% | 6.5% | 4.6% |
| 2013-10-01 | 7.2% | 7.2% | 7.0% | 7.6% | 6.9% | 8.6% | 6.4% | 7.6% | 6.2% | 8.2% | 7.2% | 7.8% | 4.7% | 6.8% | 8.8% | 6.9% | 4.5% | 5.1% | 7.8% | 6.0% | 6.4% | 6.3% | 6.5% | 8.5% | 4.8% | 8.3% | 6.6% | 5.2% | 3.5% | 9.4% | 5.1% | 7.8% | 6.9% | 7.5% | 6.6% | 2.8% | 7.3% | 5.1% | 7.3% | 6.8% | 9.4% | 6.8% | 3.6% | 7.4% | 6.1% | 4.0% | 4.3% | 5.5% | 6.5% | 6.7% | 6.4% | 4.6% |
| 2013-11-01 | 6.9% | 7.2% | 6.9% | 7.5% | 6.7% | 8.5% | 6.2% | 7.5% | 6.1% | 8.1% | 7.1% | 7.7% | 4.7% | 6.4% | 8.7% | 6.7% | 4.5% | 5.0% | 7.7% | 5.9% | 6.3% | 6.2% | 6.4% | 8.4% | 4.8% | 8.2% | 6.6% | 5.1% | 3.5% | 9.3% | 5.0% | 7.6% | 6.9% | 7.3% | 6.5% | 2.8% | 7.1% | 5.0% | 7.2% | 6.7% | 9.3% | 6.5% | 3.5% | 7.3% | 6.0% | 4.0% | 4.2% | 5.4% | 6.4% | 6.7% | 6.3% | 4.6% |
| 2013-12-01 | 6.7% | 7.2% | 6.9% | 7.4% | 6.6% | 8.4% | 6.1% | 7.4% | 6.1% | 8.0% | 7.0% | 7.6% | 4.6% | 6.0% | 8.6% | 6.5% | 4.5% | 4.9% | 7.6% | 5.7% | 6.2% | 6.1% | 6.3% | 8.2% | 4.7% | 8.1% | 6.6% | 5.0% | 3.5% | 9.1% | 4.9% | 7.5% | 6.8% | 7.1% | 6.4% | 2.8% | 6.9% | 5.0% | 7.2% | 6.6% | 9.1% | 6.3% | 3.5% | 7.1% | 5.8% | 3.9% | 4.1% | 5.4% | 6.3% | 6.7% | 6.1% | 4.6% |
| 2014-01-01 | 6.6% | 7.2% | 6.9% | 7.2% | 6.5% | 8.2% | 6.0% | 7.2% | 6.0% | 7.9% | 6.9% | 7.5% | 4.6% | 5.6% | 8.4% | 6.4% | 4.4% | 4.8% | 7.5% | 5.6% | 6.1% | 6.1% | 6.2% | 8.1% | 4.7% | 8.1% | 6.6% | 5.0% | 3.5% | 8.9% | 4.8% | 7.3% | 6.8% | 7.0% | 6.4% | 2.7% | 6.6% | 4.9% | 7.2% | 6.5% | 8.9% | 6.1% | 3.5% | 6.9% | 5.7% | 3.8% | 4.1% | 5.3% | 6.2% | 6.7% | 6.0% | 4.5% |
| 2014-02-01 | 6.7% | 7.1% | 6.9% | 7.1% | 6.3% | 8.1% | 5.8% | 7.1% | 6.0% | 7.9% | 6.8% | 7.4% | 4.5% | 5.2% | 8.1% | 6.3% | 4.4% | 4.7% | 7.3% | 5.6% | 6.0% | 6.0% | 6.1% | 8.0% | 4.6% | 8.0% | 6.6% | 4.9% | 3.5% | 8.8% | 4.7% | 7.1% | 6.7% | 6.8% | 6.3% | 2.7% | 6.4% | 4.7% | 7.1% | 6.4% | 8.7% | 6.0% | 3.4% | 6.8% | 5.6% | 3.7% | 4.0% | 5.3% | 6.1% | 6.7% | 5.9% | 4.4% |
| 2014-03-01 | 6.7% | 7.1% | 6.9% | 7.0% | 6.2% | 8.0% | 5.6% | 6.9% | 5.9% | 7.8% | 6.7% | 7.4% | 4.4% | 4.9% | 7.9% | 6.2% | 4.4% | 4.7% | 7.2% | 5.7% | 5.9% | 5.9% | 6.0% | 7.9% | 4.6% | 7.9% | 6.5% | 4.8% | 3.4% | 8.6% | 4.6% | 7.0% | 6.7% | 6.7% | 6.3% | 2.6% | 6.2% | 4.6% | 7.0% | 6.3% | 8.5% | 6.0% | 3.4% | 6.8% | 5.5% | 3.7% | 4.0% | 5.3% | 6.1% | 6.7% | 5.7% | 4.4% |
| 2014-04-01 | 6.2% | 7.0% | 6.9% | 6.9% | 6.0% | 7.8% | 5.4% | 6.8% | 5.8% | 7.8% | 6.7% | 7.4% | 4.4% | 4.6% | 7.6% | 6.1% | 4.3% | 4.6% | 7.0% | 5.8% | 5.8% | 5.9% | 5.9% | 7.7% | 4.5% | 7.9% | 6.4% | 4.7% | 3.4% | 8.5% | 4.5% | 6.8% | 6.7% | 6.5% | 6.3% | 2.6% | 6.0% | 4.5% | 6.9% | 6.2% | 8.3% | 6.0% | 3.4% | 6.7% | 5.4% | 3.6% | 4.0% | 5.3% | 6.0% | 6.6% | 5.6% | 4.4% |
| 2014-05-01 | 6.3% | 6.9% | 6.9% | 6.9% | 6.0% | 7.7% | 5.2% | 6.7% | 5.8% | 7.8% | 6.6% | 7.3% | 4.4% | 4.5% | 7.4% | 6.1% | 4.3% | 4.6% | 6.7% | 6.0% | 5.7% | 5.8% | 5.9% | 7.5% | 4.4% | 7.8% | 6.3% | 4.7% | 3.3% | 8.3% | 4.4% | 6.7% | 6.7% | 6.4% | 6.2% | 2.6% | 5.9% | 4.4% | 6.8% | 6.1% | 8.0% | 6.1% | 3.4% | 6.7% | 5.3% | 3.6% | 4.0% | 5.2% | 6.0% | 6.5% | 5.5% | 4.4% |
| 2014-06-01 | 6.1% | 6.8% | 6.9% | 6.8% | 5.9% | 7.6% | 5.0% | 6.6% | 5.7% | 7.8% | 6.5% | 7.3% | 4.3% | 4.0% | 7.2% | 6.0% | 4.3% | 4.5% | 6.5% | 6.2% | 5.6% | 5.8% | 5.8% | 7.4% | 4.3% | 7.7% | 6.2% | 4.7% | 3.3% | 8.2% | 4.3% | 6.7% | 6.6% | 6.3% | 6.2% | 2.6% | 5.8% | 4.3% | 6.7% | 6.0% | 7.8% | 6.2% | 3.3% | 6.7% | 5.2% | 3.6% | 4.0% | 5.2% | 5.9% | 6.5% | 5.4% | 4.4% |
| 2014-07-01 | 6.2% | 6.7% | 6.8% | 6.7% | 5.8% | 7.5% | 4.8% | 6.6% | 5.6% | 7.7% | 6.4% | 7.2% | 4.2% | 4.0% | 7.0% | 5.9% | 4.2% | 4.5% | 6.3% | 6.4% | 5.5% | 5.7% | 5.7% | 7.2% | 4.2% | 7.6% | 6.1% | 4.6% | 3.2% | 8.1% | 4.3% | 6.6% | 6.6% | 6.2% | 6.1% | 2.6% | 5.7% | 4.2% | 6.6% | 5.8% | 7.6% | 6.3% | 3.3% | 6.6% | 5.2% | 3.6% | 4.0% | 5.1% | 5.9% | 6.4% | 5.3% | 4.4% |
| 2014-08-01 | 6.1% | 6.6% | 6.8% | 6.7% | 5.7% | 7.4% | 4.6% | 6.5% | 5.5% | 7.7% | 6.3% | 7.1% | 4.1% | 4.0% | 6.8% | 5.8% | 4.2% | 4.4% | 6.0% | 6.6% | 5.4% | 5.6% | 5.6% | 7.0% | 4.1% | 7.5% | 6.0% | 4.6% | 3.2% | 7.9% | 4.2% | 6.6% | 6.6% | 6.1% | 6.1% | 2.6% | 5.6% | 4.2% | 6.5% | 5.7% | 7.4% | 6.5% | 3.3% | 6.6% | 5.1% | 3.6% | 4.0% | 5.1% | 5.9% | 6.4% | 5.1% | 4.4% |
| 2014-09-01 | 5.9% | 6.5% | 6.7% | 6.7% | 5.7% | 7.3% | 4.5% | 6.4% | 5.4% | 7.6% | 6.2% | 7.0% | 4.1% | 4.0% | 6.6% | 5.8% | 4.2% | 4.4% | 5.9% | 6.7% | 5.3% | 5.6% | 5.6% | 6.8% | 4.0% | 7.4% | 5.9% | 4.6% | 3.1% | 7.8% | 4.1% | 6.6% | 6.5% | 6.0% | 6.0% | 2.6% | 5.5% | 4.1% | 6.4% | 5.6% | 7.3% | 6.5% | 3.3% | 6.5% | 5.0% | 3.6% | 4.0% | 5.0% | 5.8% | 6.4% | 5.0% | 4.4% |
| 2014-10-01 | 5.7% | 6.4% | 6.5% | 6.6% | 5.6% | 7.2% | 4.4% | 6.3% | 5.3% | 7.6% | 6.1% | 6.8% | 4.0% | 4.0% | 6.5% | 5.7% | 4.1% | 4.3% | 5.7% | 6.8% | 5.2% | 5.5% | 5.5% | 6.6% | 4.0% | 7.2% | 5.8% | 4.5% | 3.1% | 7.7% | 4.1% | 6.5% | 6.4% | 5.9% | 5.9% | 2.6% | 5.4% | 4.1% | 6.3% | 5.6% | 7.1% | 6.6% | 3.3% | 6.4% | 4.9% | 3.6% | 4.0% | 4.9% | 5.8% | 6.4% | 5.0% | 4.3% |
| 2014-11-01 | 5.8% | 6.3% | 6.4% | 6.5% | 5.6% | 7.1% | 4.3% | 6.2% | 5.2% | 7.5% | 6.0% | 6.7% | 3.9% | 3.9% | 6.3% | 5.6% | 4.0% | 4.3% | 5.5% | 6.8% | 5.2% | 5.5% | 5.4% | 6.4% | 3.9% | 7.1% | 5.7% | 4.5% | 3.0% | 7.6% | 4.0% | 6.5% | 6.4% | 5.8% | 5.8% | 2.6% | 5.3% | 4.0% | 6.2% | 5.5% | 6.9% | 6.5% | 3.2% | 6.3% | 4.8% | 3.6% | 3.9% | 4.9% | 5.7% | 6.3% | 4.9% | 4.1% |
| 2014-12-01 | 5.6% | 6.2% | 6.3% | 6.4% | 5.5% | 6.9% | 4.2% | 6.1% | 5.1% | 7.4% | 6.0% | 6.6% | 3.9% | 3.9% | 6.2% | 5.5% | 3.9% | 4.3% | 5.4% | 6.8% | 5.0% | 5.4% | 5.2% | 6.2% | 3.9% | 6.9% | 5.7% | 4.4% | 3.0% | 7.5% | 3.9% | 6.4% | 6.4% | 5.8% | 5.7% | 2.6% | 5.2% | 4.0% | 6.0% | 5.5% | 6.7% | 6.5% | 3.2% | 6.2% | 4.6% | 3.6% | 3.9% | 4.8% | 5.7% | 6.4% | 4.8% | 4.0% |
| 2015-01-01 | 5.7% | 6.1% | 6.2% | 6.4% | 5.5% | 6.8% | 4.1% | 6.0% | 5.0% | 7.4% | 5.9% | 6.5% | 3.8% | 3.8% | 6.1% | 5.4% | 3.9% | 4.3% | 5.3% | 6.8% | 4.9% | 5.4% | 5.2% | 6.0% | 3.8% | 6.8% | 5.6% | 4.3% | 2.9% | 7.4% | 3.8% | 6.3% | 6.5% | 5.7% | 5.7% | 2.6% | 5.2% | 4.0% | 5.8% | 5.5% | 6.6% | 6.4% | 3.2% | 6.1% | 4.6% | 3.6% | 3.8% | 4.8% | 5.6% | 6.4% | 4.7% | 3.9% |
| 2015-02-01 | 5.5% | 6.1% | 6.3% | 6.3% | 5.4% | 6.7% | 4.1% | 5.9% | 4.9% | 7.3% | 5.8% | 6.4% | 3.8% | 3.9% | 6.1% | 5.2% | 3.8% | 4.4% | 5.3% | 6.7% | 4.8% | 5.3% | 5.1% | 5.9% | 3.8% | 6.7% | 5.6% | 4.3% | 2.9% | 7.3% | 3.8% | 6.3% | 6.6% | 5.6% | 5.7% | 2.6% | 5.2% | 4.1% | 5.8% | 5.5% | 6.5% | 6.4% | 3.2% | 6.1% | 4.5% | 3.5% | 3.7% | 4.7% | 5.5% | 6.5% | 4.7% | 3.9% |
| 2015-03-01 | 5.4% | 6.1% | 6.3% | 6.2% | 5.4% | 6.6% | 4.1% | 5.8% | 4.9% | 7.2% | 5.8% | 6.3% | 3.7% | 3.9% | 6.0% | 5.1% | 3.8% | 4.4% | 5.3% | 6.6% | 4.7% | 5.3% | 5.0% | 5.8% | 3.8% | 6.7% | 5.6% | 4.3% | 3.0% | 7.2% | 3.7% | 6.2% | 6.7% | 5.6% | 5.8% | 2.7% | 5.2% | 4.2% | 5.7% | 5.5% | 6.4% | 6.3% | 3.2% | 6.0% | 4.5% | 3.5% | 3.7% | 4.7% | 5.5% | 6.7% | 4.6% | 4.0% |
| 2015-04-01 | 5.4% | 6.1% | 6.3% | 6.2% | 5.3% | 6.5% | 4.0% | 5.8% | 4.9% | 7.2% | 5.7% | 6.3% | 3.6% | 3.9% | 6.0% | 4.9% | 3.8% | 4.4% | 5.3% | 6.5% | 4.6% | 5.2% | 5.0% | 5.7% | 3.8% | 6.6% | 5.5% | 4.2% | 3.0% | 7.1% | 3.6% | 6.1% | 6.7% | 5.5% | 5.8% | 2.8% | 5.1% | 4.3% | 5.7% | 5.5% | 6.3% | 6.2% | 3.1% | 5.9% | 4.5% | 3.5% | 3.6% | 4.6% | 5.4% | 6.8% | 4.6% | 4.1% |
| 2015-05-01 | 5.6% | 6.1% | 6.3% | 6.1% | 5.2% | 6.4% | 3.9% | 5.7% | 4.9% | 7.0% | 5.7% | 6.2% | 3.5% | 3.9% | 6.0% | 4.8% | 3.7% | 4.3% | 5.2% | 6.4% | 4.5% | 5.1% | 4.9% | 5.6% | 3.8% | 6.5% | 5.3% | 4.3% | 3.0% | 7.0% | 3.5% | 6.0% | 6.7% | 5.4% | 5.8% | 2.8% | 5.0% | 4.4% | 5.6% | 5.5% | 6.2% | 6.1% | 3.1% | 5.8% | 4.4% | 3.5% | 3.6% | 4.5% | 5.4% | 6.8% | 4.5% | 4.2% |
| 2015-06-01 | 5.3% | 6.2% | 6.3% | 6.1% | 5.1% | 6.3% | 3.8% | 5.6% | 4.8% | 6.9% | 5.6% | 6.1% | 3.4% | 3.9% | 6.0% | 4.7% | 3.7% | 4.2% | 5.2% | 6.3% | 4.4% | 5.0% | 4.8% | 5.5% | 3.8% | 6.4% | 5.2% | 4.3% | 3.0% | 6.9% | 3.4% | 5.8% | 6.7% | 5.3% | 5.8% | 2.8% | 4.9% | 4.4% | 5.5% | 5.4% | 6.0% | 6.0% | 3.1% | 5.7% | 4.4% | 3.5% | 3.5% | 4.4% | 5.4% | 6.8% | 4.4% | 4.2% |
| 2015-07-01 | 5.2% | 6.2% | 6.2% | 6.1% | 4.9% | 6.2% | 3.7% | 5.6% | 4.8% | 6.8% | 5.5% | 6.0% | 3.3% | 3.9% | 5.9% | 4.6% | 3.6% | 4.1% | 5.2% | 6.1% | 4.3% | 4.9% | 4.7% | 5.4% | 3.8% | 6.3% | 5.0% | 4.3% | 3.0% | 6.8% | 3.3% | 5.6% | 6.6% | 5.2% | 5.7% | 2.8% | 4.8% | 4.4% | 5.5% | 5.4% | 5.9% | 5.8% | 3.1% | 5.5% | 4.4% | 3.5% | 3.5% | 4.3% | 5.4% | 6.7% | 4.4% | 4.2% |
| 2015-08-01 | 5.1% | 6.2% | 6.2% | 6.0% | 4.8% | 6.0% | 3.6% | 5.5% | 4.7% | 6.8% | 5.4% | 5.9% | 3.3% | 3.9% | 5.9% | 4.6% | 3.6% | 4.0% | 5.2% | 6.1% | 4.2% | 4.9% | 4.7% | 5.2% | 3.8% | 6.3% | 4.9% | 4.3% | 3.0% | 6.7% | 3.3% | 5.5% | 6.6% | 5.0% | 5.7% | 2.8% | 4.8% | 4.3% | 5.4% | 5.3% | 5.8% | 5.7% | 3.0% | 5.4% | 4.5% | 3.5% | 3.5% | 4.2% | 5.4% | 6.6% | 4.3% | 4.2% |
| 2015-09-01 | 5.0% | 6.1% | 6.2% | 6.0% | 4.6% | 5.9% | 3.5% | 5.4% | 4.7% | 6.7% | 5.3% | 5.9% | 3.2% | 3.9% | 5.9% | 4.5% | 3.6% | 4.0% | 5.2% | 6.0% | 4.1% | 4.8% | 4.6% | 5.1% | 3.8% | 6.3% | 4.8% | 4.3% | 3.0% | 6.6% | 3.2% | 5.3% | 6.6% | 4.9% | 5.6% | 2.8% | 4.7% | 4.3% | 5.3% | 5.3% | 5.7% | 5.6% | 3.0% | 5.3% | 4.5% | 3.5% | 3.4% | 4.1% | 5.4% | 6.5% | 4.3% | 4.3% |
| 2015-10-01 | 5.0% | 6.1% | 6.3% | 5.9% | 4.5% | 5.8% | 3.4% | 5.4% | 4.7% | 6.6% | 5.3% | 5.8% | 3.2% | 3.8% | 5.9% | 4.5% | 3.6% | 3.9% | 5.2% | 6.0% | 4.1% | 4.7% | 4.6% | 5.0% | 3.7% | 6.4% | 4.7% | 4.3% | 3.0% | 6.5% | 3.1% | 5.2% | 6.5% | 4.9% | 5.5% | 2.8% | 4.8% | 4.3% | 5.2% | 5.3% | 5.7% | 5.5% | 2.9% | 5.1% | 4.5% | 3.5% | 3.4% | 4.1% | 5.4% | 6.4% | 4.2% | 4.3% |
| 2015-11-01 | 5.1% | 6.1% | 6.3% | 5.8% | 4.4% | 5.8% | 3.4% | 5.4% | 4.6% | 6.6% | 5.2% | 5.8% | 3.1% | 3.8% | 6.0% | 4.5% | 3.6% | 3.9% | 5.2% | 6.0% | 4.0% | 4.7% | 4.5% | 5.0% | 3.8% | 6.4% | 4.6% | 4.3% | 3.0% | 6.4% | 3.0% | 5.1% | 6.5% | 4.9% | 5.4% | 2.9% | 4.8% | 4.4% | 5.1% | 5.2% | 5.6% | 5.4% | 2.9% | 5.0% | 4.5% | 3.5% | 3.4% | 4.0% | 5.4% | 6.4% | 4.2% | 4.5% |
| 2015-12-01 | 5.0% | 6.1% | 6.4% | 5.8% | 4.3% | 5.7% | 3.3% | 5.3% | 4.6% | 6.5% | 5.1% | 5.7% | 3.1% | 3.8% | 6.1% | 4.6% | 3.6% | 3.9% | 5.2% | 6.0% | 4.0% | 4.6% | 4.4% | 4.9% | 3.8% | 6.4% | 4.5% | 4.3% | 3.0% | 6.3% | 3.0% | 5.0% | 6.5% | 4.8% | 5.4% | 3.0% | 4.9% | 4.4% | 5.0% | 5.3% | 5.6% | 5.4% | 2.8% | 4.9% | 4.5% | 3.5% | 3.3% | 4.0% | 5.4% | 6.4% | 4.2% | 4.7% |
| 2016-01-01 | 4.8% | 6.1% | 6.4% | 5.7% | 4.2% | 5.7% | 3.3% | 5.2% | 4.5% | 6.4% | 5.1% | 5.7% | 3.0% | 3.8% | 6.2% | 4.6% | 3.6% | 3.9% | 5.2% | 6.0% | 4.0% | 4.5% | 4.4% | 4.9% | 3.8% | 6.3% | 4.5% | 4.4% | 3.0% | 6.2% | 2.9% | 5.0% | 6.5% | 4.8% | 5.3% | 3.1% | 5.0% | 4.5% | 4.9% | 5.3% | 5.6% | 5.3% | 2.8% | 4.8% | 4.5% | 3.5% | 3.2% | 4.0% | 5.4% | 6.4% | 4.1% | 5.0% |
| 2016-02-01 | 4.9% | 6.0% | 6.5% | 5.6% | 4.1% | 5.6% | 3.3% | 5.2% | 4.5% | 6.3% | 5.0% | 5.7% | 3.0% | 3.8% | 6.2% | 4.6% | 3.6% | 3.9% | 5.1% | 6.1% | 3.9% | 4.4% | 4.3% | 4.9% | 3.8% | 6.2% | 4.4% | 4.4% | 3.0% | 6.2% | 2.9% | 5.0% | 6.5% | 4.8% | 5.2% | 3.2% | 5.0% | 4.5% | 4.9% | 5.3% | 5.5% | 5.3% | 2.8% | 4.7% | 4.4% | 3.5% | 3.2% | 3.9% | 5.4% | 6.3% | 4.1% | 5.3% |
| 2016-03-01 | 5.0% | 6.0% | 6.5% | 5.6% | 4.0% | 5.6% | 3.3% | 5.1% | 4.4% | 6.2% | 5.0% | 5.6% | 3.0% | 3.7% | 6.2% | 4.6% | 3.6% | 3.9% | 5.1% | 6.1% | 3.9% | 4.3% | 4.2% | 5.0% | 3.8% | 6.1% | 4.4% | 4.4% | 3.0% | 6.1% | 2.8% | 5.0% | 6.6% | 4.8% | 5.2% | 3.2% | 5.0% | 4.6% | 4.9% | 5.3% | 5.4% | 5.2% | 2.8% | 4.7% | 4.5% | 3.5% | 3.2% | 3.9% | 5.4% | 6.3% | 4.0% | 5.5% |
| 2016-04-01 | 5.1% | 5.9% | 6.5% | 5.6% | 4.0% | 5.5% | 3.3% | 5.0% | 4.4% | 6.1% | 4.9% | 5.5% | 3.0% | 3.7% | 6.1% | 4.6% | 3.6% | 4.0% | 5.0% | 6.1% | 3.9% | 4.3% | 4.1% | 5.0% | 3.8% | 6.0% | 4.5% | 4.4% | 3.0% | 6.0% | 2.8% | 5.0% | 6.6% | 4.8% | 5.1% | 3.2% | 5.0% | 4.7% | 4.9% | 5.4% | 5.4% | 5.1% | 2.9% | 4.6% | 4.5% | 3.4% | 3.1% | 3.9% | 5.3% | 6.2% | 4.0% | 5.7% |
| 2016-05-01 | 4.8% | 5.9% | 6.6% | 5.5% | 4.0% | 5.5% | 3.3% | 4.9% | 4.4% | 6.1% | 4.9% | 5.4% | 3.0% | 3.7% | 6.0% | 4.5% | 3.6% | 4.0% | 4.9% | 6.1% | 3.8% | 4.3% | 4.1% | 5.0% | 3.8% | 6.0% | 4.6% | 4.4% | 3.0% | 5.9% | 2.9% | 5.0% | 6.7% | 4.8% | 5.1% | 3.2% | 5.0% | 4.7% | 4.9% | 5.4% | 5.4% | 5.1% | 2.9% | 4.7% | 4.6% | 3.4% | 3.1% | 3.9% | 5.3% | 6.2% | 4.0% | 5.7% |
| 2016-06-01 | 4.9% | 5.9% | 6.6% | 5.5% | 4.0% | 5.5% | 3.2% | 4.9% | 4.5% | 6.1% | 4.9% | 5.4% | 2.9% | 3.7% | 5.9% | 4.4% | 3.7% | 4.0% | 4.9% | 6.1% | 3.8% | 4.3% | 4.0% | 5.0% | 3.8% | 5.9% | 4.7% | 4.3% | 3.1% | 5.8% | 2.9% | 5.0% | 6.8% | 4.9% | 5.0% | 3.2% | 5.0% | 4.8% | 4.9% | 5.4% | 5.3% | 5.0% | 3.0% | 4.7% | 4.7% | 3.4% | 3.1% | 4.0% | 5.3% | 6.2% | 3.9% | 5.6% |
| 2016-07-01 | 4.8% | 5.9% | 6.6% | 5.5% | 4.0% | 5.5% | 3.2% | 4.8% | 4.5% | 6.2% | 4.9% | 5.4% | 2.9% | 3.7% | 5.8% | 4.4% | 3.6% | 4.1% | 4.9% | 6.1% | 3.8% | 4.2% | 3.9% | 5.0% | 3.9% | 5.9% | 4.7% | 4.3% | 3.1% | 5.7% | 2.9% | 5.0% | 6.9% | 4.9% | 5.0% | 3.1% | 5.0% | 4.8% | 4.9% | 5.4% | 5.3% | 4.9% | 3.1% | 4.8% | 4.7% | 3.3% | 3.1% | 4.0% | 5.3% | 6.1% | 3.9% | 5.4% |
| 2016-08-01 | 4.9% | 5.9% | 6.7% | 5.4% | 4.0% | 5.5% | 3.1% | 4.7% | 4.5% | 6.2% | 4.9% | 5.4% | 2.9% | 3.7% | 5.8% | 4.3% | 3.6% | 4.1% | 5.0% | 6.1% | 3.7% | 4.2% | 3.9% | 5.0% | 3.9% | 5.9% | 4.7% | 4.3% | 3.1% | 5.7% | 2.9% | 5.0% | 6.9% | 5.0% | 5.1% | 3.1% | 5.0% | 4.8% | 4.8% | 5.4% | 5.2% | 4.8% | 3.1% | 4.8% | 4.7% | 3.3% | 3.1% | 4.1% | 5.2% | 6.1% | 3.9% | 5.3% |
| 2016-09-01 | 5.0% | 5.9% | 6.7% | 5.4% | 3.9% | 5.5% | 3.0% | 4.7% | 4.6% | 6.3% | 4.9% | 5.4% | 2.8% | 3.6% | 5.7% | 4.2% | 3.6% | 4.1% | 5.0% | 6.1% | 3.7% | 4.3% | 3.9% | 5.1% | 4.0% | 5.9% | 4.7% | 4.3% | 3.1% | 5.6% | 2.9% | 4.9% | 6.9% | 5.0% | 5.1% | 3.0% | 5.1% | 4.7% | 4.7% | 5.4% | 5.1% | 4.7% | 3.2% | 4.9% | 4.8% | 3.3% | 3.1% | 4.1% | 5.1% | 6.0% | 3.9% | 5.2% |
| 2016-10-01 | 4.9% | 5.9% | 6.7% | 5.4% | 3.9% | 5.5% | 3.0% | 4.7% | 4.6% | 6.3% | 4.9% | 5.4% | 2.8% | 3.6% | 5.7% | 4.1% | 3.5% | 4.1% | 5.1% | 6.1% | 3.7% | 4.3% | 3.9% | 5.1% | 4.0% | 5.9% | 4.6% | 4.3% | 3.2% | 5.6% | 2.9% | 4.9% | 6.9% | 5.0% | 5.1% | 3.0% | 5.2% | 4.7% | 4.5% | 5.3% | 5.0% | 4.6% | 3.2% | 4.9% | 4.8% | 3.2% | 3.1% | 4.1% | 5.1% | 5.9% | 3.8% | 5.2% |
| 2016-11-01 | 4.7% | 5.8% | 6.7% | 5.3% | 3.9% | 5.4% | 2.9% | 4.6% | 4.7% | 6.3% | 4.8% | 5.4% | 2.7% | 3.6% | 5.6% | 4.1% | 3.5% | 4.1% | 5.1% | 6.0% | 3.6% | 4.2% | 3.9% | 5.1% | 4.0% | 5.8% | 4.5% | 4.2% | 3.1% | 5.5% | 2.9% | 4.8% | 6.9% | 4.9% | 5.0% | 3.0% | 5.3% | 4.6% | 4.4% | 5.3% | 4.9% | 4.5% | 3.2% | 4.8% | 4.8% | 3.2% | 3.1% | 4.1% | 5.0% | 5.8% | 3.7% | 5.1% |
| 2016-12-01 | 4.7% | 5.7% | 6.7% | 5.3% | 3.8% | 5.4% | 2.7% | 4.6% | 4.7% | 6.3% | 4.8% | 5.3% | 2.7% | 3.5% | 5.4% | 4.0% | 3.4% | 4.0% | 5.1% | 5.9% | 3.5% | 4.2% | 3.9% | 5.0% | 3.9% | 5.7% | 4.3% | 4.2% | 3.1% | 5.4% | 2.9% | 4.7% | 6.8% | 4.8% | 5.0% | 2.9% | 5.3% | 4.5% | 4.3% | 5.2% | 4.8% | 4.5% | 3.2% | 4.7% | 4.8% | 3.2% | 3.1% | 4.0% | 4.9% | 5.6% | 3.6% | 5.0% |
| 2017-01-01 | 4.7% | 5.5% | 6.6% | 5.2% | 3.8% | 5.2% | 2.6% | 4.6% | 4.7% | 6.3% | 4.7% | 5.2% | 2.6% | 3.5% | 5.3% | 3.8% | 3.3% | 3.9% | 5.1% | 5.8% | 3.5% | 4.1% | 3.8% | 4.8% | 3.8% | 5.6% | 4.2% | 4.2% | 3.1% | 5.4% | 2.9% | 4.6% | 6.7% | 4.7% | 4.9% | 2.9% | 5.3% | 4.4% | 4.1% | 5.2% | 4.6% | 4.4% | 3.1% | 4.6% | 4.8% | 3.2% | 3.1% | 4.0% | 4.8% | 5.4% | 3.5% | 4.8% |
| 2017-02-01 | 4.6% | 5.2% | 6.6% | 5.2% | 3.7% | 5.1% | 2.5% | 4.5% | 4.6% | 6.2% | 4.6% | 5.1% | 2.6% | 3.4% | 5.1% | 3.7% | 3.2% | 3.8% | 5.0% | 5.7% | 3.4% | 4.0% | 3.8% | 4.7% | 3.7% | 5.5% | 4.1% | 4.1% | 3.0% | 5.3% | 2.9% | 4.5% | 6.6% | 4.6% | 4.7% | 2.8% | 5.2% | 4.3% | 4.0% | 5.1% | 4.5% | 4.3% | 3.1% | 4.4% | 4.7% | 3.2% | 3.1% | 4.0% | 4.7% | 5.2% | 3.4% | 4.6% |
| 2017-03-01 | 4.4% | 5.0% | 6.5% | 5.1% | 3.7% | 5.0% | 2.4% | 4.5% | 4.6% | 6.2% | 4.5% | 5.0% | 2.5% | 3.3% | 5.0% | 3.5% | 3.2% | 3.7% | 5.0% | 5.5% | 3.4% | 4.0% | 3.8% | 4.5% | 3.6% | 5.4% | 3.9% | 4.1% | 3.0% | 5.2% | 2.8% | 4.5% | 6.5% | 4.6% | 4.6% | 2.7% | 5.1% | 4.2% | 3.9% | 5.1% | 4.5% | 4.2% | 3.1% | 4.2% | 4.6% | 3.2% | 3.1% | 3.9% | 4.6% | 5.1% | 3.3% | 4.4% |
| 2017-04-01 | 4.4% | 4.8% | 6.5% | 5.0% | 3.7% | 5.0% | 2.4% | 4.5% | 4.6% | 6.2% | 4.4% | 4.9% | 2.5% | 3.2% | 4.9% | 3.4% | 3.1% | 3.6% | 5.0% | 5.4% | 3.4% | 3.9% | 3.8% | 4.3% | 3.5% | 5.4% | 3.8% | 4.1% | 2.9% | 5.1% | 2.8% | 4.4% | 6.4% | 4.6% | 4.5% | 2.6% | 5.1% | 4.1% | 3.9% | 5.0% | 4.4% | 4.2% | 3.0% | 3.9% | 4.5% | 3.2% | 3.1% | 3.8% | 4.6% | 5.0% | 3.3% | 4.2% |
| 2017-05-01 | 4.4% | 4.6% | 6.5% | 5.0% | 3.7% | 4.9% | 2.4% | 4.4% | 4.5% | 6.2% | 4.3% | 4.8% | 2.4% | 3.2% | 4.9% | 3.4% | 3.1% | 3.6% | 4.9% | 5.2% | 3.4% | 3.9% | 3.8% | 4.3% | 3.5% | 5.3% | 3.7% | 4.1% | 2.9% | 5.0% | 2.8% | 4.5% | 6.2% | 4.6% | 4.5% | 2.5% | 5.0% | 4.0% | 4.0% | 5.0% | 4.4% | 4.1% | 3.0% | 3.7% | 4.4% | 3.2% | 3.0% | 3.7% | 4.6% | 5.0% | 3.2% | 4.1% |
| 2017-06-01 | 4.3% | 4.4% | 6.5% | 4.9% | 3.7% | 4.9% | 2.5% | 4.4% | 4.5% | 6.1% | 4.3% | 4.8% | 2.3% | 3.1% | 4.9% | 3.4% | 3.1% | 3.6% | 4.9% | 5.1% | 3.4% | 3.9% | 3.8% | 4.4% | 3.5% | 5.3% | 3.7% | 4.1% | 2.9% | 4.9% | 2.7% | 4.5% | 6.1% | 4.6% | 4.5% | 2.5% | 5.0% | 4.0% | 4.0% | 4.9% | 4.4% | 4.1% | 3.0% | 3.6% | 4.3% | 3.2% | 3.0% | 3.7% | 4.6% | 5.1% | 3.3% | 4.1% |
| 2017-07-01 | 4.3% | 4.3% | 6.5% | 4.9% | 3.7% | 4.8% | 2.6% | 4.4% | 4.5% | 6.1% | 4.2% | 4.7% | 2.1% | 3.1% | 5.0% | 3.5% | 3.1% | 3.6% | 4.8% | 4.9% | 3.4% | 4.0% | 3.8% | 4.5% | 3.4% | 5.2% | 3.6% | 4.1% | 2.9% | 4.8% | 2.8% | 4.5% | 6.0% | 4.7% | 4.5% | 2.5% | 5.0% | 4.0% | 4.1% | 4.9% | 4.5% | 4.2% | 3.1% | 3.5% | 4.2% | 3.2% | 2.9% | 3.6% | 4.6% | 5.1% | 3.3% | 4.2% |
| 2017-08-01 | 4.4% | 4.2% | 6.5% | 4.8% | 3.7% | 4.8% | 2.7% | 4.4% | 4.4% | 6.1% | 4.2% | 4.6% | 2.0% | 3.2% | 5.0% | 3.5% | 3.0% | 3.6% | 4.8% | 4.8% | 3.4% | 4.0% | 3.8% | 4.6% | 3.4% | 5.2% | 3.6% | 4.1% | 3.0% | 4.8% | 2.8% | 4.6% | 5.8% | 4.7% | 4.5% | 2.5% | 4.9% | 4.0% | 4.1% | 4.9% | 4.5% | 4.2% | 3.1% | 3.4% | 4.2% | 3.2% | 2.9% | 3.5% | 4.6% | 5.2% | 3.3% | 4.3% |
| 2017-09-01 | 4.3% | 4.1% | 6.5% | 4.9% | 3.8% | 4.7% | 2.8% | 4.4% | 4.4% | 6.0% | 4.2% | 4.6% | 1.9% | 3.2% | 4.9% | 3.5% | 3.0% | 3.6% | 4.6% | 4.8% | 3.4% | 4.0% | 3.8% | 4.7% | 3.4% | 5.1% | 3.6% | 4.1% | 3.0% | 4.8% | 2.8% | 4.6% | 5.7% | 4.7% | 4.5% | 2.5% | 4.9% | 3.9% | 4.2% | 4.9% | 4.6% | 4.2% | 3.1% | 3.4% | 4.1% | 3.1% | 2.9% | 3.5% | 4.7% | 5.3% | 3.2% | 4.3% |
| 2017-10-01 | 4.2% | 4.0% | 6.5% | 4.9% | 3.8% | 4.6% | 2.8% | 4.3% | 4.3% | 6.0% | 4.1% | 4.5% | 1.9% | 3.2% | 4.9% | 3.5% | 2.9% | 3.5% | 4.5% | 4.7% | 3.3% | 4.1% | 3.8% | 4.8% | 3.4% | 5.0% | 3.6% | 4.1% | 3.0% | 4.8% | 2.8% | 4.6% | 5.6% | 4.7% | 4.4% | 2.6% | 4.8% | 3.9% | 4.2% | 4.9% | 4.6% | 4.2% | 3.0% | 3.4% | 4.1% | 3.1% | 3.0% | 3.5% | 4.7% | 5.3% | 3.2% | 4.3% |
| 2017-11-01 | 4.2% | 4.0% | 6.5% | 4.9% | 3.8% | 4.5% | 2.8% | 4.3% | 4.3% | 5.9% | 4.1% | 4.5% | 1.9% | 3.1% | 4.8% | 3.4% | 2.9% | 3.5% | 4.4% | 4.7% | 3.2% | 4.1% | 3.8% | 4.7% | 3.3% | 4.9% | 3.6% | 4.0% | 3.0% | 4.8% | 2.8% | 4.6% | 5.5% | 4.6% | 4.4% | 2.6% | 4.7% | 3.8% | 4.1% | 4.9% | 4.6% | 4.2% | 3.0% | 3.4% | 4.1% | 3.1% | 3.0% | 3.4% | 4.6% | 5.4% | 3.1% | 4.3% |
| 2017-12-01 | 4.1% | 4.0% | 6.4% | 4.9% | 3.8% | 4.5% | 2.8% | 4.3% | 4.2% | 5.9% | 4.0% | 4.4% | 1.9% | 3.1% | 4.7% | 3.3% | 2.8% | 3.4% | 4.3% | 4.7% | 3.1% | 4.0% | 3.7% | 4.6% | 3.3% | 4.9% | 3.5% | 4.0% | 3.0% | 4.9% | 2.8% | 4.5% | 5.4% | 4.5% | 4.3% | 2.6% | 4.6% | 3.8% | 4.1% | 4.9% | 4.5% | 4.1% | 3.0% | 3.5% | 4.1% | 3.1% | 3.0% | 3.4% | 4.6% | 5.4% | 3.0% | 4.3% |
| 2018-01-01 | 4.0% | 4.0% | 6.3% | 4.8% | 3.8% | 4.4% | 2.8% | 4.2% | 4.2% | 5.9% | 4.0% | 4.3% | 2.1% | 3.0% | 4.5% | 3.3% | 2.7% | 3.4% | 4.2% | 4.7% | 3.0% | 3.9% | 3.7% | 4.5% | 3.2% | 4.9% | 3.5% | 3.9% | 2.9% | 4.9% | 2.7% | 4.4% | 5.2% | 4.5% | 4.2% | 2.6% | 4.6% | 3.7% | 4.1% | 4.8% | 4.5% | 3.9% | 2.9% | 3.5% | 4.1% | 3.0% | 3.0% | 3.3% | 4.6% | 5.4% | 2.9% | 4.2% |
| 2018-02-01 | 4.1% | 4.0% | 6.2% | 4.8% | 3.7% | 4.3% | 2.9% | 4.2% | 4.1% | 5.9% | 3.9% | 4.3% | 2.2% | 2.9% | 4.4% | 3.3% | 2.7% | 3.3% | 4.2% | 4.8% | 3.0% | 3.8% | 3.6% | 4.4% | 3.2% | 4.9% | 3.4% | 3.9% | 2.9% | 4.8% | 2.7% | 4.3% | 5.1% | 4.4% | 4.1% | 2.6% | 4.5% | 3.6% | 4.0% | 4.7% | 4.3% | 3.7% | 2.9% | 3.5% | 4.0% | 3.0% | 2.9% | 3.2% | 4.5% | 5.4% | 2.9% | 4.1% |
| 2018-03-01 | 4.0% | 4.0% | 6.1% | 4.7% | 3.7% | 4.3% | 2.9% | 4.1% | 4.0% | 5.8% | 3.9% | 4.2% | 2.3% | 2.9% | 4.4% | 3.3% | 2.6% | 3.3% | 4.2% | 4.8% | 2.9% | 3.7% | 3.6% | 4.3% | 3.1% | 4.9% | 3.3% | 3.8% | 2.9% | 4.7% | 2.7% | 4.2% | 5.0% | 4.3% | 4.0% | 2.5% | 4.5% | 3.5% | 4.0% | 4.6% | 4.2% | 3.5% | 2.9% | 3.5% | 4.0% | 3.0% | 2.9% | 3.1% | 4.5% | 5.4% | 2.9% | 4.0% |
| 2018-04-01 | 4.0% | 4.0% | 6.0% | 4.7% | 3.6% | 4.2% | 2.9% | 4.0% | 3.9% | 5.8% | 3.8% | 4.1% | 2.4% | 2.8% | 4.3% | 3.3% | 2.5% | 3.3% | 4.2% | 4.9% | 3.0% | 3.6% | 3.5% | 4.1% | 3.1% | 4.9% | 3.2% | 3.8% | 2.8% | 4.5% | 2.7% | 4.2% | 4.9% | 4.2% | 4.0% | 2.5% | 4.5% | 3.4% | 3.9% | 4.5% | 4.1% | 3.3% | 2.8% | 3.5% | 4.0% | 3.0% | 2.8% | 3.0% | 4.4% | 5.3% | 3.0% | 4.0% |
| 2018-05-01 | 3.8% | 3.9% | 5.9% | 4.7% | 3.6% | 4.2% | 3.0% | 4.0% | 3.8% | 5.7% | 3.7% | 4.0% | 2.4% | 2.8% | 4.3% | 3.4% | 2.5% | 3.2% | 4.2% | 4.9% | 3.0% | 3.6% | 3.5% | 4.1% | 3.0% | 4.9% | 3.1% | 3.8% | 2.8% | 4.3% | 2.7% | 4.1% | 4.8% | 4.1% | 3.9% | 2.4% | 4.5% | 3.3% | 3.9% | 4.4% | 4.0% | 3.3% | 2.8% | 3.5% | 3.9% | 2.9% | 2.7% | 2.9% | 4.4% | 5.2% | 3.0% | 4.0% |
| 2018-06-01 | 4.0% | 3.9% | 5.9% | 4.7% | 3.6% | 4.2% | 3.1% | 3.9% | 3.7% | 5.6% | 3.7% | 4.0% | 2.4% | 2.8% | 4.2% | 3.4% | 2.4% | 3.2% | 4.2% | 4.9% | 3.1% | 3.6% | 3.5% | 4.0% | 3.0% | 4.9% | 3.0% | 3.7% | 2.8% | 4.2% | 2.6% | 4.0% | 4.7% | 4.0% | 3.9% | 2.3% | 4.5% | 3.2% | 3.9% | 4.4% | 4.0% | 3.3% | 2.8% | 3.5% | 3.9% | 2.9% | 2.6% | 2.8% | 4.3% | 5.2% | 3.0% | 4.0% |
| 2018-07-01 | 3.8% | 3.9% | 5.9% | 4.7% | 3.5% | 4.2% | 3.1% | 3.9% | 3.7% | 5.4% | 3.6% | 3.9% | 2.4% | 2.8% | 4.3% | 3.4% | 2.4% | 3.2% | 4.2% | 4.8% | 3.2% | 3.6% | 3.4% | 4.0% | 3.0% | 4.8% | 3.0% | 3.7% | 2.9% | 4.0% | 2.6% | 4.0% | 4.7% | 4.0% | 3.9% | 2.2% | 4.5% | 3.1% | 3.9% | 4.3% | 3.9% | 3.3% | 2.7% | 3.5% | 3.9% | 2.9% | 2.6% | 2.8% | 4.3% | 5.1% | 3.0% | 4.1% |
| 2018-08-01 | 3.8% | 3.9% | 5.8% | 4.8% | 3.5% | 4.2% | 3.1% | 3.8% | 3.6% | 5.4% | 3.6% | 3.9% | 2.3% | 2.9% | 4.3% | 3.5% | 2.5% | 3.2% | 4.2% | 4.8% | 3.2% | 3.6% | 3.4% | 4.1% | 3.0% | 4.9% | 3.0% | 3.7% | 2.9% | 4.0% | 2.6% | 3.9% | 4.7% | 3.9% | 4.0% | 2.2% | 4.4% | 3.1% | 4.0% | 4.3% | 4.0% | 3.3% | 2.7% | 3.5% | 3.8% | 2.9% | 2.5% | 2.7% | 4.3% | 5.0% | 3.0% | 4.1% |
| 2018-09-01 | 3.7% | 3.9% | 5.8% | 4.9% | 3.6% | 4.2% | 3.1% | 3.8% | 3.6% | 5.4% | 3.5% | 3.9% | 2.3% | 2.9% | 4.4% | 3.5% | 2.5% | 3.3% | 4.2% | 4.8% | 3.3% | 3.7% | 3.3% | 4.1% | 3.1% | 4.9% | 3.0% | 3.7% | 3.0% | 4.1% | 2.6% | 3.8% | 4.8% | 3.9% | 4.0% | 2.2% | 4.5% | 3.1% | 4.1% | 4.3% | 4.0% | 3.3% | 2.7% | 3.5% | 3.8% | 2.9% | 2.4% | 2.8% | 4.4% | 5.0% | 3.0% | 4.1% |
| 2018-10-01 | 3.8% | 3.9% | 5.9% | 4.9% | 3.6% | 4.3% | 3.1% | 3.8% | 3.5% | 5.5% | 3.5% | 3.9% | 2.4% | 3.0% | 4.4% | 3.5% | 2.5% | 3.3% | 4.2% | 4.8% | 3.3% | 3.7% | 3.3% | 4.2% | 3.2% | 5.1% | 3.1% | 3.7% | 3.0% | 4.2% | 2.6% | 3.7% | 4.9% | 3.9% | 4.1% | 2.3% | 4.5% | 3.1% | 4.2% | 4.3% | 4.0% | 3.3% | 2.7% | 3.5% | 3.8% | 2.9% | 2.4% | 2.9% | 4.5% | 5.0% | 3.0% | 4.1% |
| 2018-11-01 | 3.8% | 3.8% | 5.9% | 5.0% | 3.7% | 4.3% | 3.1% | 3.8% | 3.6% | 5.7% | 3.6% | 3.9% | 2.5% | 3.0% | 4.5% | 3.5% | 2.5% | 3.3% | 4.2% | 4.8% | 3.2% | 3.6% | 3.3% | 4.2% | 3.4% | 5.2% | 3.1% | 3.7% | 3.0% | 4.3% | 2.6% | 3.6% | 5.0% | 4.0% | 4.1% | 2.3% | 4.5% | 3.2% | 4.2% | 4.4% | 4.0% | 3.3% | 2.8% | 3.5% | 3.8% | 2.9% | 2.3% | 2.9% | 4.6% | 5.1% | 3.0% | 4.0% |
| 2018-12-01 | 3.9% | 3.8% | 5.9% | 5.0% | 3.7% | 4.3% | 3.0% | 3.7% | 3.6% | 5.8% | 3.6% | 3.9% | 2.6% | 3.0% | 4.5% | 3.5% | 2.5% | 3.3% | 4.2% | 4.8% | 3.1% | 3.6% | 3.3% | 4.2% | 3.4% | 5.3% | 3.2% | 3.6% | 3.0% | 4.5% | 2.6% | 3.6% | 5.1% | 4.0% | 4.0% | 2.3% | 4.5% | 3.2% | 4.2% | 4.4% | 3.9% | 3.3% | 2.8% | 3.5% | 3.8% | 2.8% | 2.3% | 3.0% | 4.6% | 5.1% | 3.0% | 3.9% |
| 2019-01-01 | 4.0% | 3.7% | 5.8% | 5.0% | 3.6% | 4.3% | 2.9% | 3.7% | 3.6% | 5.9% | 3.5% | 3.9% | 2.7% | 3.0% | 4.5% | 3.5% | 2.5% | 3.3% | 4.2% | 4.8% | 3.0% | 3.5% | 3.2% | 4.2% | 3.4% | 5.3% | 3.2% | 3.6% | 3.0% | 4.5% | 2.6% | 3.5% | 5.2% | 3.9% | 3.9% | 2.3% | 4.4% | 3.2% | 4.2% | 4.4% | 3.8% | 3.2% | 2.8% | 3.5% | 3.7% | 2.8% | 2.2% | 3.0% | 4.7% | 5.0% | 3.0% | 3.7% |
| 2019-02-01 | 3.8% | 3.6% | 5.7% | 4.9% | 3.5% | 4.2% | 2.8% | 3.6% | 3.6% | 5.9% | 3.5% | 3.8% | 2.8% | 3.0% | 4.5% | 3.4% | 2.5% | 3.2% | 4.1% | 4.7% | 2.9% | 3.3% | 3.2% | 4.2% | 3.4% | 5.3% | 3.2% | 3.5% | 3.0% | 4.5% | 2.6% | 3.4% | 5.2% | 3.9% | 3.9% | 2.3% | 4.2% | 3.1% | 4.0% | 4.4% | 3.6% | 3.2% | 2.8% | 3.4% | 3.6% | 2.7% | 2.2% | 3.0% | 4.6% | 4.9% | 3.0% | 3.5% |
| 2019-03-01 | 3.8% | 3.4% | 5.6% | 4.9% | 3.4% | 4.2% | 2.7% | 3.6% | 3.6% | 5.8% | 3.4% | 3.7% | 2.9% | 2.9% | 4.3% | 3.3% | 2.5% | 3.1% | 4.1% | 4.5% | 2.7% | 3.2% | 3.1% | 4.1% | 3.4% | 5.3% | 3.1% | 3.5% | 3.0% | 4.4% | 2.5% | 3.3% | 5.1% | 3.8% | 3.8% | 2.2% | 4.1% | 3.1% | 3.9% | 4.4% | 3.5% | 3.2% | 2.8% | 3.4% | 3.5% | 2.7% | 2.1% | 3.0% | 4.6% | 4.8% | 3.1% | 3.4% |
| 2019-04-01 | 3.6% | 3.2% | 5.5% | 4.8% | 3.4% | 4.1% | 2.6% | 3.5% | 3.6% | 5.6% | 3.4% | 3.7% | 2.9% | 2.9% | 4.1% | 3.2% | 2.5% | 3.1% | 4.1% | 4.4% | 2.6% | 3.1% | 3.1% | 4.1% | 3.3% | 5.3% | 3.0% | 3.5% | 2.9% | 4.2% | 2.5% | 3.2% | 5.0% | 3.7% | 3.7% | 2.2% | 4.0% | 3.0% | 3.8% | 4.4% | 3.4% | 3.1% | 2.8% | 3.4% | 3.5% | 2.6% | 2.1% | 2.8% | 4.5% | 4.8% | 3.1% | 3.3% |
| 2019-05-01 | 3.6% | 3.1% | 5.5% | 4.8% | 3.4% | 4.1% | 2.5% | 3.5% | 3.7% | 5.4% | 3.3% | 3.6% | 2.8% | 2.9% | 4.0% | 3.2% | 2.5% | 3.1% | 4.1% | 4.3% | 2.6% | 3.1% | 3.1% | 4.1% | 3.3% | 5.4% | 2.9% | 3.5% | 2.9% | 3.9% | 2.5% | 3.2% | 4.9% | 3.7% | 3.8% | 2.1% | 3.9% | 3.0% | 3.8% | 4.3% | 3.4% | 2.9% | 2.8% | 3.3% | 3.4% | 2.6% | 2.1% | 2.7% | 4.3% | 4.7% | 3.2% | 3.4% |
| 2019-06-01 | 3.6% | 2.9% | 5.5% | 4.8% | 3.4% | 4.0% | 2.5% | 3.5% | 3.7% | 5.3% | 3.3% | 3.6% | 2.6% | 2.9% | 3.8% | 3.2% | 2.6% | 3.1% | 4.1% | 4.3% | 2.6% | 3.2% | 3.0% | 4.2% | 3.3% | 5.4% | 2.9% | 3.5% | 3.0% | 3.7% | 2.6% | 3.2% | 4.9% | 3.7% | 3.8% | 2.0% | 4.0% | 3.0% | 3.7% | 4.3% | 3.5% | 2.8% | 2.8% | 3.3% | 3.4% | 2.6% | 2.2% | 2.6% | 4.3% | 4.8% | 3.2% | 3.5% |
| 2019-07-01 | 3.7% | 2.9% | 5.5% | 4.8% | 3.4% | 4.0% | 2.5% | 3.5% | 3.8% | 5.1% | 3.2% | 3.6% | 2.4% | 3.0% | 3.8% | 3.2% | 2.6% | 3.1% | 4.1% | 4.4% | 2.7% | 3.4% | 3.0% | 4.2% | 3.3% | 5.6% | 2.9% | 3.6% | 3.1% | 3.7% | 2.6% | 3.3% | 4.8% | 3.8% | 3.9% | 2.0% | 4.1% | 3.1% | 3.7% | 4.4% | 3.6% | 2.6% | 2.9% | 3.3% | 3.5% | 2.5% | 2.3% | 2.6% | 4.2% | 4.9% | 3.3% | 3.7% |
| 2019-08-01 | 3.7% | 2.9% | 5.5% | 4.9% | 3.5% | 4.1% | 2.5% | 3.5% | 3.8% | 5.1% | 3.2% | 3.5% | 2.2% | 3.0% | 3.7% | 3.3% | 2.7% | 3.1% | 4.1% | 4.6% | 2.7% | 3.5% | 3.0% | 4.2% | 3.4% | 5.6% | 3.0% | 3.6% | 3.1% | 3.7% | 2.6% | 3.4% | 4.7% | 3.8% | 3.9% | 2.0% | 4.2% | 3.2% | 3.7% | 4.5% | 3.6% | 2.5% | 2.9% | 3.3% | 3.5% | 2.5% | 2.4% | 2.6% | 4.2% | 4.9% | 3.3% | 3.8% |
| 2019-09-01 | 3.5% | 2.9% | 5.4% | 4.8% | 3.5% | 4.1% | 2.5% | 3.5% | 3.8% | 5.0% | 3.1% | 3.5% | 2.0% | 3.0% | 3.7% | 3.3% | 2.7% | 3.1% | 4.1% | 4.7% | 2.8% | 3.6% | 3.0% | 4.1% | 3.5% | 5.6% | 3.1% | 3.6% | 3.2% | 3.8% | 2.7% | 3.5% | 4.7% | 3.9% | 3.9% | 2.1% | 4.3% | 3.2% | 3.6% | 4.5% | 3.6% | 2.4% | 2.8% | 3.4% | 3.6% | 2.5% | 2.5% | 2.6% | 4.2% | 5.0% | 3.3% | 4.0% |
| 2019-10-01 | 3.6% | 3.0% | 5.3% | 4.8% | 3.5% | 4.1% | 2.5% | 3.5% | 3.8% | 4.9% | 3.0% | 3.5% | 1.9% | 3.0% | 3.7% | 3.3% | 2.7% | 3.1% | 4.0% | 4.8% | 2.9% | 3.7% | 3.0% | 4.0% | 3.6% | 5.5% | 3.2% | 3.6% | 3.2% | 3.9% | 2.7% | 3.5% | 4.8% | 3.9% | 3.9% | 2.1% | 4.3% | 3.2% | 3.5% | 4.6% | 3.6% | 2.5% | 2.8% | 3.4% | 3.5% | 2.5% | 2.6% | 2.7% | 4.1% | 5.0% | 3.3% | 4.1% |
| 2019-11-01 | 3.6% | 3.1% | 5.2% | 4.9% | 3.5% | 4.1% | 2.6% | 3.5% | 3.7% | 5.0% | 2.9% | 3.4% | 1.9% | 3.0% | 3.6% | 3.3% | 2.7% | 3.1% | 4.0% | 4.9% | 2.9% | 3.7% | 3.0% | 3.9% | 3.6% | 5.5% | 3.3% | 3.7% | 3.1% | 3.9% | 2.7% | 3.6% | 4.9% | 3.9% | 3.8% | 2.0% | 4.3% | 3.1% | 3.4% | 4.6% | 3.5% | 2.5% | 2.7% | 3.5% | 3.5% | 2.5% | 2.6% | 2.7% | 4.0% | 5.0% | 3.2% | 4.2% |
| 2019-12-01 | 3.6% | 3.2% | 5.2% | 4.9% | 3.5% | 4.1% | 2.6% | 3.5% | 3.7% | 5.1% | 2.9% | 3.5% | 2.0% | 3.0% | 3.6% | 3.3% | 2.6% | 3.1% | 4.0% | 5.1% | 2.9% | 3.8% | 3.0% | 3.8% | 3.7% | 5.5% | 3.3% | 3.7% | 3.1% | 3.8% | 2.7% | 3.6% | 5.1% | 3.9% | 3.8% | 2.0% | 4.4% | 3.1% | 3.4% | 4.7% | 3.6% | 2.6% | 2.7% | 3.6% | 3.5% | 2.5% | 2.6% | 2.7% | 3.9% | 5.0% | 3.2% | 4.4% |
| 2020-01-01 | 3.5% | 3.3% | 5.2% | 5.0% | 3.5% | 4.1% | 2.7% | 3.4% | 3.7% | 5.3% | 2.8% | 3.5% | 2.1% | 3.0% | 3.7% | 3.4% | 2.6% | 3.1% | 4.0% | 5.2% | 2.9% | 4.0% | 3.0% | 3.8% | 3.8% | 5.5% | 3.3% | 3.7% | 3.0% | 3.8% | 2.7% | 3.5% | 5.2% | 3.9% | 3.7% | 2.1% | 4.5% | 3.1% | 3.4% | 4.8% | 3.6% | 2.8% | 2.7% | 3.6% | 3.4% | 2.5% | 2.5% | 2.6% | 3.9% | 5.1% | 3.1% | 4.7% |
| 2020-02-01 | 3.5% | 3.4% | 5.2% | 5.0% | 3.6% | 4.1% | 2.8% | 3.4% | 3.7% | 5.4% | 2.7% | 3.6% | 2.2% | 3.0% | 3.8% | 3.4% | 2.6% | 3.1% | 4.1% | 5.2% | 2.8% | 4.2% | 2.9% | 3.8% | 3.9% | 5.7% | 3.3% | 3.7% | 3.0% | 4.0% | 2.7% | 3.5% | 5.4% | 3.9% | 3.7% | 2.2% | 4.6% | 3.2% | 3.4% | 5.0% | 3.7% | 2.9% | 2.6% | 3.6% | 3.5% | 2.6% | 2.6% | 2.7% | 3.9% | 5.1% | 3.0% | 4.9% |
| 2020-03-01 | 4.4% | 3.6% | 5.2% | 5.1% | 4.9% | 5.5% | 4.8% | 3.4% | 5.0% | 5.5% | 4.5% | 3.7% | 2.2% | 2.8% | 4.9% | 3.5% | 2.6% | 3.1% | 4.1% | 6.8% | 2.7% | 4.2% | 2.9% | 3.8% | 4.0% | 5.8% | 3.5% | 3.6% | 4.3% | 8.0% | 2.6% | 3.3% | 6.1% | 3.9% | 3.9% | 2.5% | 4.8% | 3.2% | 3.5% | 5.2% | 3.6% | 3.0% | 2.5% | 3.6% | 5.1% | 2.5% | 2.7% | 2.9% | 5.3% | 5.2% | 2.9% | 5.2% |
| 2020-04-01 | 14.7% | 13.7% | 11.9% | 13.9% | 10.0% | 15.9% | 11.6% | 8.0% | 13.1% | 11.1% | 13.2% | 12.3% | 22.4% | 11.8% | 17.4% | 16.8% | 10.5% | 12.2% | 16.5% | 13.5% | 9.1% | 9.5% | 17.1% | 22.7% | 9.0% | 15.4% | 11.2% | 12.2% | 8.2% | 28.5% | 16.2% | 15.5% | 9.5% | 16.2% | 14.2% | 8.3% | 16.4% | 12.6% | 13.3% | 16.5% | 18.4% | 11.6% | 8.8% | 15.9% | 12.6% | 10.0% | 14.3% | 11.6% | 16.8% | 15.5% | 14.1% | 5.4% |
| 2020-05-01 | 13.2% | 10.4% | 11.9% | 11.0% | 8.7% | 16.1% | 11.8% | 11.4% | 13.3% | 9.0% | 13.9% | 9.6% | 20.9% | 8.9% | 14.5% | 12.3% | 8.0% | 9.0% | 12.6% | 12.3% | 9.2% | 9.5% | 15.5% | 19.2% | 10.8% | 11.0% | 9.2% | 9.1% | 6.3% | 23.4% | 11.8% | 15.8% | 9.8% | 16.5% | 11.5% | 7.0% | 12.7% | 9.7% | 12.2% | 13.1% | 15.6% | 9.1% | 6.6% | 12.1% | 11.8% | 7.6% | 9.5% | 9.6% | 13.2% | 12.2% | 10.4% | 8.6% |
| 2020-06-01 | 11.0% | 8.7% | 11.3% | 9.5% | 7.6% | 14.1% | 11.0% | 11.1% | 12.7% | 8.8% | 11.6% | 8.4% | 17.7% | 7.3% | 12.7% | 10.2% | 6.5% | 7.2% | 5.1% | 11.0% | 6.6% | 8.6% | 14.4% | 14.6% | 8.7% | 9.2% | 7.7% | 7.4% | 5.1% | 18.5% | 9.7% | 14.5% | 9.5% | 13.7% | 9.6% | 6.4% | 11.0% | 8.0% | 10.5% | 11.5% | 13.5% | 7.8% | 5.3% | 10.1% | 10.1% | 6.2% | 7.6% | 8.5% | 11.4% | 10.4% | 8.6% | 7.2% |
| 2020-07-01 | 10.2% | 7.7% | 11.2% | 8.6% | 7.1% | 13.4% | 6.6% | 11.2% | 7.7% | 9.0% | 12.5% | 7.7% | 16.2% | 6.3% | 11.5% | 8.8% | 5.8% | 6.4% | 5.7% | 10.5% | 6.3% | 8.1% | 12.7% | 12.6% | 7.9% | 8.2% | 7.0% | 6.5% | 4.4% | 16.8% | 8.3% | 14.3% | 9.6% | 12.7% | 8.6% | 6.2% | 9.9% | 7.2% | 9.5% | 10.6% | 12.2% | 7.2% | 4.8% | 8.8% | 9.3% | 5.4% | 6.4% | 7.9% | 10.2% | 9.4% | 7.6% | 6.6% |
| 2020-08-01 | 8.4% | 6.6% | 7.8% | 7.6% | 6.2% | 11.9% | 6.2% | 9.5% | 7.5% | 8.8% | 8.9% | 6.9% | 13.9% | 5.3% | 9.8% | 7.2% | 5.1% | 5.6% | 5.2% | 9.4% | 4.6% | 7.2% | 10.6% | 9.9% | 6.9% | 7.4% | 6.4% | 5.4% | 3.7% | 14.7% | 6.8% | 12.8% | 9.3% | 11.0% | 7.2% | 5.8% | 8.4% | 6.2% | 8.1% | 9.5% | 10.2% | 6.3% | 4.3% | 7.5% | 8.1% | 4.6% | 5.1% | 7.0% | 8.7% | 8.3% | 6.2% | 5.9% |
| 2020-09-01 | 7.9% | 6.1% | 7.7% | 7.2% | 5.8% | 10.3% | 6.4% | 8.9% | 7.6% | 8.7% | 8.7% | 6.4% | 14.2% | 4.8% | 9.0% | 6.3% | 4.8% | 5.2% | 5.1% | 8.9% | 4.4% | 6.8% | 9.9% | 8.7% | 6.2% | 7.1% | 6.0% | 5.0% | 3.3% | 13.6% | 6.1% | 8.3% | 8.8% | 10.3% | 6.5% | 5.6% | 7.6% | 5.8% | 7.5% | 8.9% | 9.6% | 5.9% | 4.0% | 6.9% | 7.7% | 4.3% | 4.5% | 6.3% | 7.9% | 7.6% | 5.7% | 5.6% |
| 2020-10-01 | 6.9% | 5.3% | 7.3% | 6.7% | 5.4% | 9.5% | 6.1% | 8.1% | 5.3% | 8.2% | 7.2% | 5.6% | 12.1% | 4.3% | 8.1% | 5.5% | 4.5% | 4.7% | 4.9% | 8.0% | 4.1% | 6.2% | 8.6% | 7.5% | 5.5% | 6.8% | 5.5% | 4.5% | 2.9% | 12.1% | 5.2% | 7.5% | 8.4% | 9.3% | 5.8% | 5.3% | 6.8% | 5.4% | 6.8% | 8.3% | 6.9% | 5.3% | 3.7% | 6.1% | 7.1% | 3.9% | 4.0% | 5.6% | 7.1% | 6.9% | 5.0% | 5.3% |
| 2020-11-01 | 6.7% | 4.8% | 7.2% | 6.5% | 5.2% | 9.2% | 6.2% | 7.8% | 5.4% | 7.8% | 6.7% | 5.3% | 10.8% | 4.2% | 7.7% | 5.1% | 4.5% | 4.4% | 4.9% | 7.4% | 4.1% | 6.1% | 8.1% | 7.1% | 5.0% | 6.8% | 5.3% | 4.2% | 2.8% | 11.2% | 4.8% | 7.5% | 8.0% | 9.1% | 5.6% | 5.1% | 6.5% | 5.3% | 6.6% | 8.0% | 6.8% | 5.1% | 3.6% | 5.7% | 6.9% | 3.7% | 3.8% | 5.2% | 6.7% | 6.5% | 4.8% | 5.2% |
| 2020-12-01 | 6.7% | 4.4% | 7.3% | 6.3% | 5.0% | 9.2% | 6.4% | 7.7% | 5.6% | 7.5% | 6.5% | 5.1% | 9.8% | 4.2% | 7.5% | 4.8% | 4.5% | 4.2% | 4.9% | 7.0% | 4.4% | 6.3% | 7.7% | 7.0% | 4.6% | 6.7% | 5.1% | 4.0% | 2.8% | 10.8% | 4.5% | 7.4% | 7.9% | 8.8% | 5.6% | 5.0% | 6.2% | 5.2% | 6.6% | 7.7% | 6.7% | 4.9% | 3.5% | 5.5% | 6.9% | 3.5% | 3.8% | 5.0% | 6.5% | 6.2% | 4.7% | 5.1% |
| 2021-01-01 | 6.4% | 4.0% | 7.1% | 6.1% | 4.9% | 8.8% | 6.2% | 7.3% | 5.7% | 6.9% | 6.0% | 4.8% | 8.3% | 4.0% | 7.1% | 4.5% | 4.4% | 3.8% | 4.8% | 6.5% | 4.4% | 5.9% | 7.1% | 6.4% | 4.2% | 6.6% | 5.0% | 3.8% | 2.7% | 10.2% | 4.2% | 7.3% | 7.4% | 8.6% | 5.5% | 4.7% | 6.0% | 5.0% | 6.4% | 7.5% | 6.3% | 4.6% | 3.3% | 5.2% | 6.7% | 3.3% | 3.9% | 4.8% | 6.3% | 5.9% | 4.5% | 5.1% |
| 2021-02-01 | 6.2% | 3.8% | 7.0% | 6.0% | 4.8% | 8.6% | 6.2% | 7.2% | 5.7% | 6.7% | 5.6% | 4.6% | 7.3% | 4.0% | 6.9% | 4.3% | 4.4% | 3.6% | 4.7% | 6.3% | 4.6% | 5.7% | 6.7% | 6.3% | 3.9% | 6.5% | 4.9% | 3.7% | 2.7% | 9.8% | 4.0% | 7.2% | 7.3% | 8.4% | 5.4% | 4.5% | 5.8% | 4.8% | 6.2% | 7.3% | 6.1% | 4.4% | 3.2% | 5.0% | 6.6% | 3.1% | 3.9% | 4.6% | 6.1% | 5.8% | 4.4% | 5.0% |
| 2021-03-01 | 6.0% | 3.7% | 7.0% | 5.8% | 4.6% | 8.4% | 6.1% | 7.0% | 5.8% | 6.6% | 5.4% | 4.4% | 6.6% | 3.9% | 6.7% | 4.2% | 4.4% | 3.5% | 4.7% | 6.1% | 4.8% | 5.7% | 6.4% | 6.2% | 3.7% | 6.4% | 4.8% | 3.6% | 2.6% | 9.2% | 3.9% | 6.9% | 7.2% | 7.9% | 5.2% | 4.3% | 5.7% | 4.7% | 6.1% | 7.1% | 6.0% | 4.3% | 3.2% | 4.9% | 6.4% | 3.0% | 3.8% | 4.5% | 5.8% | 5.6% | 4.3% | 5.0% |
| 2021-04-01 | 6.0% | 3.6% | 7.0% | 5.6% | 4.5% | 8.3% | 6.1% | 7.0% | 5.8% | 6.8% | 5.1% | 4.3% | 6.3% | 3.8% | 6.6% | 4.1% | 4.5% | 3.5% | 4.7% | 6.1% | 5.0% | 5.7% | 6.3% | 6.2% | 3.5% | 6.2% | 4.7% | 3.6% | 2.6% | 8.6% | 3.8% | 7.0% | 7.3% | 7.8% | 5.1% | 4.0% | 5.6% | 4.5% | 5.9% | 6.9% | 6.1% | 4.2% | 3.2% | 4.8% | 6.2% | 2.9% | 3.7% | 4.3% | 5.7% | 5.5% | 4.3% | 4.8% |
| 2021-05-01 | 5.8% | 3.6% | 6.8% | 5.4% | 4.4% | 7.9% | 5.8% | 6.7% | 5.7% | 6.9% | 4.9% | 4.1% | 5.9% | 3.7% | 6.5% | 4.0% | 4.5% | 3.4% | 4.7% | 5.9% | 4.9% | 5.7% | 5.9% | 6.2% | 3.4% | 6.0% | 4.5% | 3.6% | 2.5% | 7.8% | 3.7% | 6.6% | 7.2% | 7.4% | 5.0% | 3.8% | 5.4% | 4.4% | 5.6% | 6.7% | 6.0% | 4.1% | 3.2% | 4.6% | 5.9% | 2.8% | 3.6% | 4.1% | 5.5% | 5.4% | 4.1% | 4.7% |
| 2021-06-01 | 5.9% | 3.5% | 6.8% | 5.2% | 4.2% | 7.9% | 5.9% | 6.7% | 5.7% | 7.2% | 4.8% | 4.0% | 5.9% | 3.7% | 6.5% | 3.9% | 4.5% | 3.5% | 4.8% | 5.8% | 5.0% | 6.1% | 6.0% | 6.3% | 3.4% | 5.8% | 4.4% | 3.6% | 2.5% | 7.2% | 3.6% | 7.1% | 7.3% | 7.4% | 5.0% | 3.6% | 5.3% | 4.2% | 5.4% | 6.6% | 6.2% | 4.1% | 3.2% | 4.4% | 5.9% | 2.8% | 3.5% | 4.0% | 5.4% | 5.3% | 4.0% | 4.6% |
| 2021-07-01 | 5.4% | 3.4% | 6.5% | 4.9% | 4.0% | 7.4% | 5.6% | 6.3% | 5.5% | 7.1% | 4.5% | 3.9% | 5.5% | 3.6% | 6.2% | 3.7% | 4.4% | 3.4% | 4.8% | 5.5% | 4.9% | 6.1% | 5.7% | 6.2% | 3.3% | 5.6% | 4.3% | 3.5% | 2.5% | 6.6% | 3.5% | 6.6% | 7.0% | 6.9% | 4.9% | 3.4% | 5.1% | 3.9% | 5.1% | 6.4% | 6.0% | 4.0% | 3.2% | 4.2% | 5.6% | 2.7% | 3.3% | 3.8% | 5.2% | 5.1% | 3.8% | 4.5% |
| 2021-08-01 | 5.2% | 3.3% | 6.3% | 4.5% | 3.8% | 7.0% | 5.3% | 6.1% | 5.3% | 6.9% | 4.3% | 3.7% | 5.3% | 3.5% | 6.0% | 3.4% | 4.3% | 3.2% | 4.8% | 5.2% | 4.8% | 6.2% | 5.5% | 6.0% | 3.3% | 5.3% | 4.1% | 3.4% | 2.5% | 6.0% | 3.4% | 6.5% | 6.8% | 6.6% | 4.8% | 3.3% | 4.9% | 3.5% | 4.9% | 6.1% | 5.8% | 3.9% | 3.2% | 4.0% | 5.4% | 2.6% | 3.2% | 3.6% | 5.0% | 4.8% | 3.6% | 4.3% |
| 2021-09-01 | 4.7% | 3.2% | 5.9% | 4.2% | 3.5% | 6.4% | 4.7% | 5.6% | 5.0% | 6.5% | 3.9% | 3.5% | 4.8% | 3.4% | 5.5% | 3.1% | 4.1% | 3.0% | 4.7% | 4.8% | 4.5% | 5.8% | 5.1% | 5.7% | 3.2% | 5.0% | 4.0% | 3.2% | 2.5% | 5.6% | 3.2% | 5.8% | 6.2% | 6.0% | 4.5% | 3.2% | 4.7% | 3.2% | 4.5% | 5.8% | 5.4% | 3.8% | 3.1% | 3.8% | 5.1% | 2.5% | 3.2% | 3.4% | 4.8% | 4.6% | 3.4% | 4.2% |
| 2021-10-01 | 4.6% | 3.1% | 5.7% | 3.9% | 3.4% | 6.1% | 4.5% | 5.4% | 4.9% | 6.3% | 3.7% | 3.4% | 4.7% | 3.2% | 5.3% | 2.8% | 4.0% | 2.9% | 4.6% | 4.6% | 4.4% | 5.7% | 5.0% | 5.4% | 3.1% | 4.7% | 4.0% | 3.0% | 2.4% | 5.4% | 3.1% | 5.5% | 6.1% | 5.7% | 4.4% | 3.2% | 4.5% | 2.9% | 4.4% | 5.6% | 5.0% | 3.6% | 3.0% | 3.7% | 5.0% | 2.3% | 3.1% | 3.4% | 4.6% | 4.3% | 3.2% | 4.0% |
| 2021-11-01 | 4.2% | 3.1% | 5.5% | 3.9% | 3.3% | 5.8% | 4.3% | 5.2% | 4.8% | 6.1% | 3.5% | 3.3% | 4.4% | 3.2% | 5.1% | 2.7% | 3.9% | 2.8% | 4.6% | 4.5% | 4.2% | 5.4% | 4.8% | 5.2% | 3.1% | 4.7% | 3.9% | 2.9% | 2.4% | 5.3% | 3.0% | 5.1% | 6.0% | 5.4% | 4.2% | 3.1% | 4.5% | 2.8% | 4.2% | 5.5% | 4.7% | 3.6% | 2.9% | 3.6% | 4.9% | 2.3% | 3.1% | 3.3% | 4.5% | 4.3% | 3.1% | 4.0% |
| 2021-12-01 | 3.9% | 3.1% | 5.5% | 3.9% | 3.3% | 5.8% | 4.2% | 5.1% | 4.8% | 6.1% | 3.5% | 3.3% | 4.3% | 3.1% | 5.1% | 2.7% | 3.9% | 2.8% | 4.6% | 4.4% | 4.1% | 5.4% | 4.6% | 5.1% | 3.0% | 4.7% | 3.9% | 2.9% | 2.3% | 5.3% | 3.0% | 5.1% | 5.9% | 5.4% | 4.1% | 3.1% | 4.5% | 2.8% | 4.2% | 5.5% | 4.5% | 3.6% | 2.9% | 3.6% | 4.8% | 2.3% | 3.1% | 3.3% | 4.5% | 4.3% | 3.1% | 4.0% |
| 2022-01-01 | 4.0% | 3.1% | 5.6% | 3.7% | 3.2% | 5.7% | 4.2% | 5.3% | 4.8% | 6.3% | 3.5% | 3.2% | 4.3% | 3.0% | 5.0% | 2.4% | 3.7% | 2.6% | 4.4% | 4.3% | 4.1% | 5.4% | 4.8% | 4.9% | 2.9% | 4.6% | 3.8% | 2.7% | 2.2% | 5.2% | 2.9% | 5.1% | 5.9% | 5.3% | 3.9% | 3.1% | 4.3% | 2.7% | 4.2% | 5.4% | 4.2% | 3.5% | 2.8% | 3.5% | 4.8% | 2.2% | 3.0% | 3.3% | 4.4% | 4.1% | 3.0% | 3.8% |
| 2022-02-01 | 3.8% | 3.0% | 5.3% | 3.6% | 3.1% | 5.3% | 4.0% | 4.9% | 4.6% | 6.1% | 3.3% | 3.2% | 4.2% | 2.8% | 4.8% | 2.3% | 3.5% | 2.5% | 4.2% | 4.3% | 4.0% | 5.0% | 4.7% | 4.7% | 2.7% | 4.5% | 3.7% | 2.6% | 2.1% | 5.1% | 2.7% | 4.6% | 5.6% | 4.9% | 3.7% | 2.9% | 4.2% | 2.6% | 4.0% | 5.1% | 3.9% | 3.5% | 2.6% | 3.4% | 4.7% | 2.1% | 2.9% | 3.2% | 4.3% | 3.9% | 2.9% | 3.6% |
| 2022-03-01 | 3.6% | 2.9% | 4.9% | 3.3% | 3.1% | 4.8% | 3.7% | 4.6% | 4.5% | 6.0% | 3.2% | 3.1% | 4.1% | 2.7% | 4.7% | 2.2% | 3.3% | 2.4% | 4.0% | 4.2% | 3.6% | 4.6% | 4.3% | 4.4% | 2.5% | 4.2% | 3.6% | 2.3% | 2.0% | 5.0% | 2.4% | 4.2% | 5.3% | 4.6% | 3.5% | 2.9% | 4.1% | 2.7% | 3.8% | 4.9% | 3.4% | 3.4% | 2.5% | 3.2% | 4.4% | 2.0% | 2.6% | 3.0% | 4.1% | 3.7% | 2.8% | 3.4% |
| 2022-04-01 | 3.6% | 2.8% | 4.8% | 3.2% | 3.2% | 4.6% | 3.6% | 4.4% | 4.5% | 5.8% | 3.0% | 3.1% | 4.1% | 2.6% | 4.6% | 2.2% | 3.0% | 2.4% | 3.9% | 4.1% | 3.3% | 4.2% | 4.1% | 4.3% | 2.2% | 4.1% | 3.4% | 2.3% | 1.9% | 5.0% | 2.3% | 4.1% | 5.3% | 4.5% | 3.4% | 2.8% | 4.0% | 2.7% | 3.7% | 4.8% | 3.2% | 3.3% | 2.3% | 3.2% | 4.3% | 1.9% | 2.5% | 3.0% | 4.1% | 3.6% | 2.8% | 3.3% |
| 2022-05-01 | 3.6% | 2.7% | 4.6% | 3.2% | 3.2% | 4.3% | 3.5% | 4.2% | 4.5% | 5.7% | 2.9% | 3.0% | 4.1% | 2.5% | 4.6% | 2.2% | 2.7% | 2.3% | 3.8% | 4.0% | 3.2% | 4.0% | 3.9% | 4.3% | 2.0% | 3.9% | 3.1% | 2.4% | 1.9% | 4.9% | 2.1% | 3.9% | 5.1% | 4.4% | 3.4% | 2.6% | 3.9% | 2.8% | 3.5% | 4.6% | 2.9% | 3.3% | 2.3% | 3.3% | 4.2% | 2.0% | 2.3% | 3.0% | 3.9% | 3.5% | 2.9% | 3.2% |
| 2022-06-01 | 3.6% | 2.6% | 4.6% | 3.3% | 3.2% | 4.2% | 3.4% | 4.0% | 4.5% | 5.5% | 2.8% | 2.9% | 4.2% | 2.5% | 4.5% | 2.4% | 2.6% | 2.4% | 3.7% | 3.8% | 3.0% | 4.0% | 3.7% | 4.3% | 1.8% | 3.8% | 2.8% | 2.6% | 1.9% | 4.7% | 2.0% | 3.9% | 4.9% | 4.4% | 3.4% | 2.5% | 3.9% | 2.9% | 3.5% | 4.5% | 2.7% | 3.2% | 2.3% | 3.3% | 4.1% | 2.0% | 2.2% | 2.8% | 3.8% | 3.6% | 2.9% | 3.1% |
| 2022-07-01 | 3.5% | 2.6% | 4.5% | 3.3% | 3.3% | 3.9% | 3.3% | 3.7% | 4.4% | 5.2% | 2.7% | 2.8% | 4.0% | 2.6% | 4.4% | 2.6% | 2.5% | 2.4% | 3.7% | 3.7% | 2.8% | 3.9% | 3.5% | 4.2% | 1.8% | 3.6% | 2.5% | 2.7% | 2.0% | 4.4% | 2.0% | 3.7% | 4.5% | 4.3% | 3.4% | 2.3% | 3.9% | 2.9% | 3.5% | 4.3% | 2.7% | 3.2% | 2.3% | 3.3% | 4.0% | 2.0% | 2.1% | 2.7% | 3.7% | 3.7% | 3.0% | 3.0% |
| 2022-08-01 | 3.7% | 2.6% | 4.6% | 3.5% | 3.4% | 4.1% | 3.4% | 4.1% | 4.5% | 5.1% | 2.7% | 2.8% | 4.0% | 2.7% | 4.5% | 2.8% | 2.6% | 2.5% | 3.8% | 3.5% | 3.1% | 4.3% | 3.6% | 4.1% | 1.9% | 3.6% | 2.5% | 2.8% | 2.1% | 4.4% | 2.0% | 4.0% | 4.4% | 4.7% | 3.5% | 2.3% | 4.0% | 3.1% | 3.7% | 4.2% | 2.8% | 3.1% | 2.3% | 3.4% | 4.1% | 2.0% | 2.1% | 2.6% | 3.7% | 3.9% | 3.1% | 3.1% |
| 2022-09-01 | 3.5% | 2.6% | 4.4% | 3.7% | 3.5% | 3.8% | 3.4% | 4.0% | 4.3% | 4.7% | 2.5% | 2.8% | 3.5% | 2.8% | 4.5% | 2.8% | 2.7% | 2.6% | 3.8% | 3.4% | 3.3% | 4.0% | 3.4% | 4.1% | 2.0% | 3.6% | 2.4% | 2.9% | 2.2% | 4.4% | 2.2% | 3.3% | 4.2% | 4.3% | 3.6% | 2.2% | 4.0% | 3.2% | 3.8% | 4.1% | 3.1% | 3.2% | 2.3% | 3.4% | 4.0% | 2.1% | 2.1% | 2.6% | 3.7% | 4.0% | 3.2% | 3.3% |
| 2022-10-01 | 3.7% | 2.6% | 3.8% | 4.1% | 3.5% | 4.1% | 2.8% | 4.0% | 4.7% | 4.2% | 2.7% | 3.1% | 3.7% | 2.8% | 4.6% | 3.2% | 3.1% | 3.0% | 4.0% | 3.6% | 3.1% | 3.2% | 3.8% | 4.4% | 3.0% | 4.1% | 2.7% | 2.7% | 2.7% | 5.5% | 2.9% | 3.3% | 3.5% | 4.2% | 3.9% | 2.1% | 4.2% | 3.2% | 4.8% | 4.4% | 3.4% | 3.3% | 2.2% | 3.5% | 3.9% | 2.4% | 3.1% | 3.1% | 4.6% | 4.1% | 3.0% | 3.9% |
| 2022-11-01 | 3.6% | 2.6% | 3.7% | 4.0% | 3.5% | 4.1% | 2.8% | 4.0% | 4.7% | 4.2% | 2.7% | 3.1% | 3.7% | 2.8% | 4.6% | 3.2% | 3.1% | 2.9% | 3.9% | 3.6% | 3.1% | 3.1% | 3.7% | 4.4% | 3.0% | 4.1% | 2.7% | 2.7% | 2.7% | 5.5% | 2.9% | 3.3% | 3.5% | 4.1% | 3.9% | 2.1% | 4.1% | 3.2% | 4.8% | 4.4% | 3.3% | 3.3% | 2.2% | 3.5% | 3.8% | 2.4% | 3.1% | 3.2% | 4.6% | 4.1% | 3.0% | 3.9% |
| 2022-12-01 | 3.5% | 2.6% | 3.7% | 4.0% | 3.4% | 4.1% | 2.8% | 4.0% | 4.6% | 4.2% | 2.7% | 3.1% | 3.7% | 2.8% | 4.6% | 3.1% | 3.0% | 2.9% | 3.9% | 3.5% | 3.1% | 3.0% | 3.7% | 4.3% | 2.9% | 4.0% | 2.7% | 2.6% | 2.7% | 5.5% | 2.9% | 3.3% | 3.5% | 4.1% | 3.8% | 2.1% | 4.1% | 3.2% | 4.8% | 4.3% | 3.2% | 3.3% | 2.2% | 3.5% | 3.8% | 2.4% | 3.0% | 3.1% | 4.5% | 4.1% | 3.0% | 3.9% |
| 2023-01-01 | 3.4% | 2.6% | 3.8% | 3.8% | 3.4% | 4.2% | 2.8% | 3.9% | 4.6% | 4.5% | 2.6% | 3.1% | 3.6% | 2.7% | 4.5% | 3.1% | 3.0% | 2.9% | 3.9% | 3.5% | 2.9% | 3.0% | 3.5% | 4.3% | 2.9% | 3.9% | 2.7% | 2.5% | 2.5% | 5.5% | 2.8% | 3.4% | 3.5% | 4.2% | 3.8% | 2.1% | 4.0% | 3.1% | 4.8% | 4.3% | 3.1% | 3.2% | 2.1% | 3.5% | 3.9% | 2.4% | 2.9% | 3.2% | 4.6% | 3.9% | 2.9% | 3.9% |
| 2023-02-01 | 3.6% | 2.5% | 3.8% | 3.7% | 3.2% | 4.4% | 2.9% | 4.0% | 4.6% | 4.7% | 2.6% | 3.1% | 3.6% | 2.6% | 4.5% | 3.1% | 2.9% | 2.9% | 3.9% | 3.6% | 2.8% | 2.9% | 3.7% | 4.3% | 3.0% | 3.7% | 2.6% | 2.4% | 2.3% | 5.5% | 2.7% | 3.5% | 3.6% | 4.2% | 3.6% | 2.1% | 3.9% | 3.0% | 4.7% | 4.4% | 3.1% | 3.2% | 2.1% | 3.5% | 4.0% | 2.4% | 2.8% | 3.2% | 4.6% | 3.7% | 2.7% | 3.8% |
| 2023-03-01 | 3.5% | 2.3% | 3.7% | 3.5% | 3.0% | 4.4% | 2.8% | 3.9% | 4.4% | 4.8% | 2.6% | 3.1% | 3.5% | 2.6% | 4.4% | 3.1% | 2.8% | 2.9% | 3.8% | 3.6% | 2.6% | 2.7% | 3.5% | 4.1% | 2.8% | 3.5% | 2.5% | 2.3% | 2.1% | 5.5% | 2.4% | 3.5% | 3.5% | 4.1% | 3.5% | 2.1% | 3.8% | 3.0% | 4.4% | 4.2% | 3.1% | 3.2% | 1.9% | 3.4% | 4.0% | 2.4% | 2.7% | 3.2% | 4.5% | 3.4% | 2.5% | 3.7% |
| 2023-04-01 | 3.4% | 2.2% | 3.7% | 3.4% | 2.8% | 4.5% | 2.8% | 3.8% | 4.3% | 5.0% | 2.6% | 3.1% | 3.3% | 2.6% | 4.2% | 3.0% | 2.7% | 2.9% | 3.7% | 3.6% | 2.4% | 2.5% | 3.1% | 3.8% | 2.8% | 3.4% | 2.5% | 2.3% | 2.0% | 5.4% | 2.1% | 3.5% | 3.5% | 4.0% | 3.4% | 2.1% | 3.7% | 2.9% | 4.0% | 4.1% | 3.0% | 3.1% | 1.9% | 3.3% | 4.0% | 2.3% | 2.4% | 3.1% | 4.3% | 3.3% | 2.4% | 3.5% |
| 2023-05-01 | 3.7% | 2.2% | 3.6% | 3.4% | 2.7% | 4.5% | 2.8% | 3.7% | 4.2% | 5.1% | 2.6% | 3.2% | 3.1% | 2.6% | 4.1% | 3.1% | 2.7% | 2.9% | 3.8% | 3.6% | 2.4% | 2.4% | 2.8% | 3.7% | 2.9% | 3.2% | 2.5% | 2.3% | 1.9% | 5.4% | 1.9% | 3.6% | 3.5% | 3.9% | 3.4% | 2.1% | 3.6% | 2.8% | 3.7% | 4.0% | 3.0% | 3.1% | 1.9% | 3.3% | 4.1% | 2.3% | 2.1% | 2.9% | 4.1% | 3.3% | 2.4% | 3.3% |
| 2023-06-01 | 3.6% | 2.2% | 3.7% | 3.5% | 2.6% | 4.6% | 2.8% | 3.7% | 4.2% | 5.1% | 2.6% | 3.2% | 3.0% | 2.7% | 4.0% | 3.2% | 2.7% | 2.8% | 3.8% | 3.6% | 2.4% | 2.0% | 2.6% | 3.6% | 2.9% | 3.1% | 2.6% | 2.4% | 1.9% | 5.4% | 1.8% | 3.7% | 3.5% | 3.9% | 3.3% | 2.0% | 3.4% | 2.7% | 3.5% | 3.8% | 2.9% | 3.1% | 1.8% | 3.2% | 4.1% | 2.4% | 1.9% | 2.7% | 3.8% | 3.3% | 2.5% | 3.1% |
| 2023-07-01 | 3.5% | 2.1% | 3.8% | 3.6% | 2.6% | 4.6% | 2.9% | 3.6% | 4.1% | 5.0% | 2.7% | 3.2% | 2.8% | 2.8% | 4.0% | 3.3% | 2.7% | 2.7% | 3.8% | 3.4% | 2.4% | 1.8% | 2.5% | 3.6% | 3.0% | 3.0% | 2.7% | 2.5% | 2.0% | 5.3% | 1.7% | 3.9% | 3.6% | 3.9% | 3.3% | 2.0% | 3.3% | 2.7% | 3.4% | 3.5% | 2.8% | 3.1% | 1.9% | 3.1% | 4.1% | 2.4% | 1.8% | 2.5% | 3.6% | 3.4% | 2.6% | 3.0% |
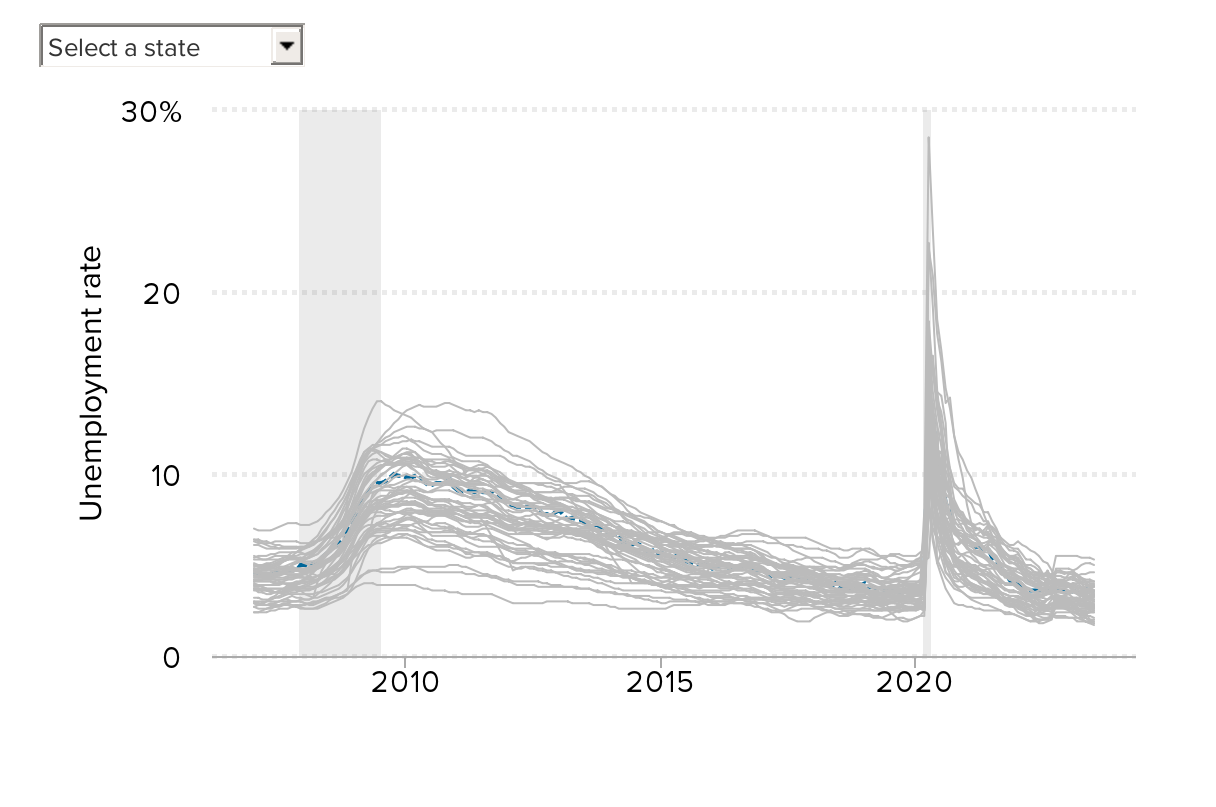
Notes: Shaded areas represent recessions.
Source: EPI/EARN analysis of Bureau of Labor Statistics Local Area Unemployment data.
State employment relative to January 2007: Choose a state to show employment growth over time for that state and all other states in the same Census division. (The dashed line shows values for the U.S.)
| date | United States | Alabama | Alaska | Arizona | Arkansas | California | Colorado | Connecticut | Delaware | District of Columbia | Florida | Georgia | Hawaii | Idaho | Illinois | Indiana | Iowa | Kansas | Kentucky | Louisiana | Maine | Maryland | Massachusetts | Michigan | Minnesota | Mississippi | Missouri | Montana | Nebraska | Nevada | New Hampshire | New Jersey | New Mexico | New York | North Carolina | North Dakota | Ohio | Oklahoma | Oregon | Pennsylvania | Rhode Island | South Carolina | South Dakota | Tennessee | Texas | Utah | Vermont | Virginia | Washington | West Virginia | Wisconsin | Wyoming |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007-01-01 | 99.3% | 99.2% | 99.3% | 99.4% | 99.5% | 99.5% | 98.0% | 99.1% | 99.5% | 98.6% | 101.3% | 99.7% | 99.1% | 98.7% | 99.7% | 99.9% | 99.2% | 98.6% | 99.7% | 98.0% | 99.4% | 99.7% | 99.3% | 100.8% | 99.8% | 99.3% | 99.5% | 98.6% | 98.6% | 99.7% | 99.4% | 99.8% | 98.6% | 99.1% | 98.6% | 98.3% | 100.4% | 98.3% | 99.1% | 99.6% | 101.6% | 99.6% | 98.7% | 99.4% | 97.2% | 97.5% | 99.8% | 99.6% | 97.8% | 99.5% | 99.7% | 96.6% |
| 2007-02-01 | 99.4% | 99.4% | 99.6% | 99.7% | 99.6% | 99.7% | 98.2% | 99.1% | 99.1% | 99.2% | 101.4% | 99.8% | 99.3% | 99.1% | 99.6% | 99.5% | 99.2% | 98.7% | 99.6% | 98.4% | 99.4% | 99.5% | 99.3% | 101.0% | 99.9% | 99.3% | 99.5% | 98.8% | 98.7% | 100.3% | 99.6% | 99.5% | 98.9% | 99.1% | 98.8% | 98.2% | 100.0% | 98.6% | 99.4% | 99.4% | 101.4% | 99.5% | 98.9% | 99.4% | 97.5% | 97.9% | 99.8% | 99.5% | 98.3% | 98.8% | 99.7% | 97.0% |
| 2007-03-01 | 99.6% | 99.6% | 99.6% | 100.0% | 100.0% | 99.9% | 98.7% | 99.1% | 99.4% | 99.2% | 101.5% | 99.9% | 99.4% | 99.4% | 99.9% | 100.0% | 99.2% | 99.4% | 99.9% | 98.8% | 99.5% | 99.8% | 99.3% | 101.0% | 100.0% | 99.1% | 100.0% | 99.4% | 98.7% | 100.4% | 99.6% | 99.7% | 99.4% | 99.2% | 99.1% | 98.6% | 100.3% | 99.2% | 99.7% | 99.6% | 101.2% | 99.7% | 99.2% | 99.7% | 97.9% | 98.4% | 100.0% | 99.7% | 98.4% | 99.4% | 99.8% | 97.5% |
| 2007-04-01 | 99.6% | 99.2% | 99.5% | 99.7% | 99.8% | 99.6% | 98.9% | 99.2% | 99.3% | 99.0% | 101.3% | 99.8% | 98.7% | 99.6% | 99.9% | 100.0% | 99.3% | 99.2% | 99.9% | 98.3% | 99.0% | 99.7% | 99.4% | 100.8% | 99.9% | 99.3% | 99.8% | 99.3% | 99.0% | 100.2% | 99.3% | 99.7% | 99.0% | 99.1% | 99.0% | 98.5% | 100.2% | 98.9% | 99.4% | 99.6% | 101.1% | 99.6% | 99.4% | 99.4% | 98.1% | 98.5% | 99.7% | 99.7% | 98.6% | 99.2% | 99.8% | 97.4% |
| 2007-05-01 | 99.7% | 99.3% | 99.6% | 99.8% | 99.8% | 99.8% | 99.0% | 99.4% | 99.6% | 98.7% | 101.2% | 99.8% | 99.6% | 99.8% | 100.0% | 99.9% | 99.5% | 99.3% | 100.2% | 98.4% | 99.1% | 99.8% | 99.6% | 100.8% | 100.0% | 99.3% | 99.9% | 99.3% | 99.2% | 100.3% | 99.7% | 99.9% | 99.1% | 99.3% | 99.2% | 98.8% | 100.3% | 99.0% | 99.5% | 99.7% | 101.3% | 99.6% | 99.6% | 99.5% | 98.4% | 98.9% | 100.0% | 99.8% | 98.9% | 99.2% | 100.0% | 97.8% |
| 2007-06-01 | 99.8% | 99.4% | 99.7% | 100.1% | 99.9% | 99.9% | 99.2% | 99.6% | 99.8% | 98.7% | 101.2% | 99.9% | 100.0% | 100.2% | 100.1% | 100.2% | 99.8% | 100.0% | 100.2% | 98.8% | 99.4% | 99.8% | 99.8% | 100.6% | 100.1% | 99.4% | 99.8% | 99.3% | 99.4% | 100.1% | 99.8% | 99.9% | 99.3% | 99.5% | 99.5% | 99.0% | 100.4% | 99.3% | 99.6% | 100.0% | 101.2% | 100.1% | 99.5% | 99.8% | 98.7% | 99.2% | 100.4% | 99.9% | 99.1% | 99.5% | 100.4% | 98.0% |
| 2007-07-01 | 99.7% | 99.4% | 99.2% | 100.1% | 99.6% | 100.2% | 99.3% | 99.8% | 99.4% | 98.9% | 100.8% | 99.8% | 99.6% | 99.9% | 100.0% | 99.9% | 99.6% | 100.0% | 99.8% | 98.7% | 99.6% | 99.9% | 99.7% | 100.4% | 100.1% | 99.2% | 99.7% | 99.7% | 99.5% | 99.8% | 99.9% | 99.9% | 99.3% | 99.5% | 99.4% | 99.1% | 100.2% | 99.4% | 99.5% | 100.0% | 101.1% | 99.8% | 99.8% | 99.8% | 98.9% | 99.3% | 100.2% | 99.9% | 99.2% | 99.4% | 100.1% | 98.2% |
| 2007-08-01 | 99.7% | 99.5% | 99.5% | 100.1% | 99.8% | 100.0% | 99.3% | 99.8% | 99.4% | 98.9% | 100.7% | 99.9% | 99.4% | 100.0% | 99.9% | 99.8% | 99.6% | 99.9% | 99.7% | 99.1% | 99.5% | 99.9% | 99.7% | 100.3% | 100.0% | 99.6% | 99.9% | 99.6% | 99.7% | 99.6% | 99.7% | 99.9% | 99.4% | 99.5% | 99.5% | 99.0% | 100.1% | 99.7% | 99.7% | 99.9% | 100.9% | 99.8% | 99.9% | 99.9% | 99.1% | 99.5% | 99.9% | 99.8% | 99.3% | 99.7% | 100.1% | 98.3% |
| 2007-09-01 | 99.8% | 99.7% | 99.7% | 100.2% | 99.8% | 100.0% | 99.6% | 99.8% | 99.3% | 99.1% | 100.5% | 99.9% | 99.8% | 99.8% | 99.9% | 100.0% | 99.7% | 100.0% | 100.1% | 99.4% | 99.6% | 99.8% | 99.7% | 100.2% | 99.9% | 99.7% | 100.0% | 99.3% | 99.7% | 99.4% | 99.7% | 99.7% | 99.5% | 99.5% | 99.6% | 99.2% | 100.0% | 99.8% | 99.6% | 99.8% | 100.4% | 100.0% | 99.8% | 99.9% | 99.3% | 99.4% | 99.8% | 99.9% | 99.4% | 99.7% | 100.1% | 98.6% |
| 2007-10-01 | 99.8% | 99.8% | 99.7% | 100.3% | 99.8% | 99.9% | 99.7% | 99.9% | 99.3% | 99.8% | 100.2% | 99.9% | 99.7% | 99.8% | 99.9% | 100.0% | 99.8% | 100.0% | 99.9% | 99.7% | 99.6% | 99.8% | 99.8% | 99.9% | 99.9% | 99.8% | 99.8% | 99.8% | 99.9% | 99.6% | 99.7% | 100.0% | 99.6% | 99.8% | 99.6% | 99.5% | 100.0% | 100.0% | 99.9% | 99.9% | 100.3% | 99.9% | 99.9% | 99.8% | 99.6% | 99.7% | 99.7% | 99.8% | 99.5% | 99.8% | 99.8% | 99.0% |
| 2007-11-01 | 99.9% | 99.8% | 99.9% | 100.1% | 99.9% | 100.0% | 99.9% | 100.0% | 99.7% | 99.7% | 100.1% | 99.9% | 99.4% | 100.0% | 100.0% | 100.1% | 100.1% | 100.2% | 100.1% | 99.8% | 100.0% | 99.9% | 100.0% | 100.0% | 100.0% | 99.8% | 100.0% | 99.8% | 99.9% | 99.7% | 99.9% | 100.0% | 99.8% | 99.9% | 99.8% | 99.9% | 100.1% | 100.2% | 99.9% | 100.0% | 100.1% | 99.9% | 100.0% | 100.0% | 99.8% | 99.9% | 99.9% | 100.0% | 99.9% | 99.8% | 99.8% | 99.6% |
| 2007-12-01 | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| 2008-01-01 | 100.0% | 99.8% | 100.7% | 99.8% | 100.0% | 99.7% | 100.1% | 100.4% | 99.9% | 99.8% | 99.5% | 100.1% | 99.8% | 99.5% | 100.2% | 99.9% | 100.2% | 100.3% | 100.2% | 99.8% | 99.9% | 100.2% | 100.2% | 99.8% | 100.1% | 100.1% | 100.2% | 100.2% | 100.4% | 99.7% | 100.4% | 100.2% | 99.8% | 100.3% | 100.1% | 100.6% | 100.2% | 100.7% | 99.9% | 100.1% | 100.0% | 100.3% | 100.7% | 100.1% | 100.3% | 99.5% | 100.1% | 100.2% | 100.2% | 100.3% | 100.2% | 100.5% |
| 2008-02-01 | 100.0% | 99.8% | 100.5% | 99.7% | 100.2% | 99.7% | 100.3% | 100.4% | 100.0% | 99.8% | 99.5% | 100.1% | 99.9% | 99.6% | 100.1% | 99.9% | 100.2% | 100.5% | 100.1% | 100.1% | 100.0% | 100.1% | 100.3% | 99.6% | 100.3% | 100.1% | 100.2% | 100.2% | 100.3% | 99.5% | 100.2% | 100.1% | 100.0% | 100.3% | 100.2% | 100.9% | 100.1% | 101.0% | 99.9% | 100.1% | 99.8% | 100.2% | 100.9% | 100.1% | 100.6% | 99.6% | 100.2% | 100.2% | 100.4% | 100.4% | 100.2% | 100.7% |
| 2008-03-01 | 99.9% | 99.6% | 100.4% | 99.2% | 100.0% | 99.6% | 100.3% | 100.5% | 99.9% | 100.2% | 99.1% | 99.9% | 99.8% | 99.7% | 99.9% | 99.5% | 100.1% | 100.6% | 99.8% | 100.0% | 100.0% | 100.0% | 100.4% | 99.2% | 100.2% | 99.9% | 100.0% | 100.3% | 100.3% | 99.3% | 100.1% | 100.1% | 100.0% | 100.3% | 100.0% | 101.2% | 99.5% | 101.0% | 99.8% | 100.0% | 99.7% | 100.0% | 100.9% | 99.9% | 100.5% | 99.5% | 100.0% | 100.1% | 100.3% | 100.0% | 100.0% | 100.8% |
| 2008-04-01 | 99.7% | 99.7% | 100.4% | 98.9% | 99.9% | 99.7% | 100.4% | 100.3% | 100.0% | 100.3% | 98.4% | 99.6% | 99.6% | 99.6% | 99.9% | 99.6% | 100.1% | 100.8% | 99.8% | 100.1% | 100.0% | 100.0% | 100.4% | 98.7% | 99.9% | 99.9% | 100.1% | 99.9% | 100.3% | 99.2% | 100.1% | 99.9% | 100.0% | 100.4% | 99.8% | 101.2% | 99.6% | 100.9% | 99.7% | 100.2% | 99.4% | 99.7% | 100.7% | 99.7% | 100.7% | 99.5% | 100.2% | 100.2% | 100.3% | 100.0% | 99.9% | 100.9% |
| 2008-05-01 | 99.6% | 99.4% | 101.1% | 98.7% | 99.8% | 99.5% | 100.4% | 100.2% | 99.4% | 100.6% | 98.0% | 99.5% | 99.5% | 99.6% | 99.8% | 99.6% | 100.2% | 100.6% | 99.8% | 100.1% | 99.9% | 99.8% | 100.3% | 98.5% | 99.9% | 99.7% | 100.1% | 99.9% | 100.3% | 99.0% | 100.0% | 99.6% | 99.9% | 100.4% | 99.6% | 101.3% | 99.5% | 100.9% | 99.5% | 100.2% | 99.2% | 99.7% | 100.8% | 99.6% | 100.8% | 99.3% | 100.2% | 100.1% | 100.2% | 101.4% | 99.9% | 101.3% |
| 2008-06-01 | 99.5% | 99.2% | 101.1% | 98.4% | 99.9% | 99.3% | 100.3% | 100.1% | 99.2% | 100.8% | 97.6% | 99.3% | 99.2% | 99.5% | 99.7% | 99.4% | 100.0% | 100.6% | 99.6% | 100.2% | 99.9% | 99.6% | 100.2% | 98.7% | 99.9% | 99.4% | 100.1% | 99.5% | 100.1% | 98.6% | 100.1% | 99.5% | 99.9% | 100.4% | 99.5% | 101.3% | 99.4% | 100.7% | 99.3% | 100.1% | 99.0% | 99.3% | 100.7% | 99.3% | 100.9% | 99.3% | 99.7% | 100.1% | 100.2% | 100.0% | 99.9% | 101.4% |
| 2008-07-01 | 99.3% | 99.1% | 101.3% | 97.8% | 99.8% | 99.1% | 100.2% | 99.8% | 99.0% | 101.4% | 97.1% | 98.9% | 98.7% | 99.5% | 99.7% | 99.2% | 100.1% | 100.4% | 99.2% | 100.1% | 99.7% | 99.6% | 100.2% | 97.9% | 99.8% | 98.6% | 99.6% | 99.7% | 100.0% | 98.1% | 100.0% | 99.2% | 99.8% | 100.5% | 99.2% | 101.8% | 99.1% | 100.9% | 99.2% | 100.0% | 98.5% | 98.6% | 100.7% | 99.0% | 101.0% | 99.2% | 99.5% | 100.1% | 100.3% | 100.3% | 99.8% | 101.5% |
| 2008-08-01 | 99.1% | 98.9% | 101.1% | 97.6% | 99.7% | 98.8% | 100.2% | 99.7% | 98.8% | 102.0% | 96.7% | 98.6% | 98.8% | 99.1% | 99.5% | 99.1% | 100.0% | 99.9% | 99.2% | 100.4% | 99.3% | 99.5% | 100.1% | 97.8% | 99.7% | 98.8% | 99.7% | 99.5% | 100.1% | 97.6% | 100.0% | 98.9% | 99.8% | 100.4% | 99.1% | 101.6% | 98.9% | 101.0% | 98.9% | 99.9% | 98.3% | 98.4% | 101.0% | 98.8% | 101.1% | 99.2% | 99.3% | 99.9% | 100.4% | 100.1% | 99.6% | 101.5% |
| 2008-09-01 | 98.8% | 98.6% | 101.3% | 97.2% | 99.7% | 98.6% | 100.0% | 99.4% | 98.4% | 101.2% | 96.3% | 98.2% | 97.8% | 98.6% | 99.2% | 98.7% | 100.0% | 100.4% | 98.6% | 99.4% | 99.0% | 99.2% | 99.9% | 97.3% | 99.6% | 98.5% | 99.6% | 99.3% | 100.1% | 97.1% | 100.0% | 98.7% | 99.9% | 100.1% | 98.9% | 101.8% | 98.6% | 101.0% | 98.7% | 99.8% | 98.1% | 98.4% | 100.9% | 98.4% | 100.8% | 99.0% | 99.4% | 99.7% | 100.1% | 100.2% | 99.8% | 101.7% |
| 2008-10-01 | 98.5% | 98.2% | 101.0% | 96.4% | 99.3% | 98.0% | 99.6% | 99.1% | 98.0% | 100.7% | 95.6% | 97.7% | 97.2% | 97.6% | 98.8% | 98.2% | 99.8% | 100.3% | 98.2% | 100.3% | 99.0% | 98.9% | 99.7% | 96.8% | 99.4% | 98.2% | 99.3% | 99.1% | 100.2% | 96.0% | 99.5% | 98.2% | 99.5% | 99.8% | 98.2% | 101.8% | 98.1% | 100.9% | 98.0% | 99.5% | 97.6% | 97.8% | 100.8% | 97.9% | 100.9% | 98.3% | 99.1% | 99.5% | 98.9% | 100.2% | 99.4% | 102.0% |
| 2008-11-01 | 97.9% | 97.4% | 100.9% | 95.7% | 98.9% | 97.3% | 99.2% | 98.7% | 97.8% | 100.5% | 95.0% | 97.1% | 97.6% | 96.7% | 98.3% | 97.6% | 99.4% | 100.1% | 97.9% | 100.4% | 98.5% | 98.6% | 99.3% | 96.1% | 98.9% | 97.8% | 98.9% | 98.9% | 100.0% | 94.9% | 99.3% | 97.7% | 99.1% | 99.5% | 97.7% | 101.9% | 97.5% | 100.7% | 97.2% | 99.1% | 97.1% | 97.2% | 100.6% | 97.3% | 100.8% | 97.8% | 99.0% | 99.1% | 99.1% | 100.1% | 99.0% | 101.7% |
| 2008-12-01 | 97.4% | 97.0% | 101.4% | 94.8% | 98.5% | 96.8% | 98.6% | 98.2% | 97.1% | 100.4% | 94.4% | 96.7% | 96.4% | 96.2% | 97.7% | 96.7% | 99.1% | 99.8% | 97.2% | 100.3% | 98.1% | 98.3% | 98.9% | 95.4% | 98.4% | 97.3% | 98.4% | 98.4% | 99.9% | 93.8% | 98.6% | 97.3% | 98.4% | 99.2% | 97.2% | 101.7% | 97.0% | 100.5% | 96.2% | 98.8% | 96.8% | 96.6% | 100.5% | 96.7% | 100.5% | 97.3% | 98.3% | 98.7% | 98.4% | 99.8% | 98.5% | 101.3% |
| 2009-01-01 | 96.9% | 95.8% | 100.7% | 94.0% | 98.1% | 95.9% | 98.2% | 97.7% | 96.5% | 100.8% | 93.4% | 95.8% | 96.1% | 95.2% | 96.9% | 95.5% | 98.6% | 99.5% | 96.2% | 99.7% | 97.6% | 97.7% | 98.0% | 93.0% | 97.8% | 96.6% | 97.8% | 97.2% | 99.5% | 92.6% | 98.4% | 96.9% | 97.7% | 98.7% | 96.0% | 101.2% | 96.1% | 99.9% | 95.3% | 98.2% | 96.0% | 95.4% | 100.2% | 95.8% | 100.0% | 96.3% | 97.7% | 98.0% | 98.0% | 99.4% | 97.6% | 100.4% |
| 2009-02-01 | 96.3% | 95.1% | 100.8% | 92.9% | 97.8% | 95.1% | 97.2% | 97.3% | 96.1% | 100.6% | 92.8% | 95.1% | 95.5% | 94.3% | 96.4% | 94.9% | 98.3% | 99.0% | 95.7% | 99.6% | 97.0% | 97.5% | 97.8% | 93.0% | 97.3% | 96.1% | 97.4% | 96.9% | 99.1% | 91.6% | 97.7% | 96.5% | 97.1% | 98.4% | 95.5% | 101.3% | 95.7% | 99.5% | 94.5% | 97.8% | 95.6% | 94.7% | 99.9% | 95.1% | 99.4% | 95.7% | 97.4% | 97.7% | 97.3% | 99.1% | 97.0% | 99.7% |
| 2009-03-01 | 95.8% | 94.6% | 100.6% | 92.2% | 97.3% | 94.5% | 96.6% | 96.6% | 95.4% | 100.1% | 92.2% | 94.5% | 95.2% | 93.6% | 95.7% | 94.3% | 97.7% | 98.3% | 95.2% | 99.1% | 96.4% | 97.0% | 97.4% | 92.4% | 96.7% | 95.3% | 96.8% | 96.0% | 98.8% | 90.5% | 97.1% | 95.9% | 96.3% | 98.0% | 94.7% | 101.1% | 95.0% | 98.9% | 93.6% | 97.2% | 95.0% | 94.0% | 99.4% | 94.3% | 98.8% | 95.0% | 96.9% | 97.2% | 96.6% | 98.6% | 96.3% | 99.1% |
| 2009-04-01 | 95.2% | 94.2% | 100.5% | 91.3% | 97.0% | 93.9% | 95.8% | 95.7% | 94.7% | 99.4% | 91.7% | 94.0% | 94.7% | 92.9% | 94.9% | 93.4% | 97.2% | 97.4% | 94.7% | 98.4% | 96.4% | 96.8% | 97.0% | 92.0% | 96.1% | 94.9% | 96.3% | 96.1% | 98.2% | 89.4% | 96.7% | 95.4% | 95.8% | 97.2% | 94.0% | 100.4% | 94.2% | 98.1% | 93.0% | 96.8% | 94.4% | 93.5% | 98.4% | 93.6% | 98.2% | 94.2% | 96.3% | 96.7% | 95.8% | 98.0% | 95.5% | 98.1% |
| 2009-05-01 | 95.0% | 93.9% | 100.4% | 91.0% | 96.4% | 93.6% | 95.7% | 95.7% | 94.9% | 99.7% | 91.4% | 93.7% | 94.4% | 92.6% | 94.7% | 93.2% | 97.1% | 97.2% | 94.7% | 98.4% | 96.4% | 96.8% | 96.9% | 91.2% | 96.0% | 94.7% | 96.1% | 96.1% | 98.2% | 88.9% | 96.9% | 95.5% | 95.7% | 97.3% | 93.9% | 101.4% | 93.8% | 97.8% | 92.8% | 96.7% | 94.5% | 93.2% | 99.1% | 93.4% | 97.9% | 94.0% | 96.6% | 96.7% | 95.7% | 98.1% | 95.4% | 98.4% |
| 2009-06-01 | 94.7% | 93.5% | 100.3% | 90.5% | 96.2% | 93.2% | 95.3% | 95.3% | 94.3% | 99.9% | 91.1% | 93.4% | 94.5% | 92.8% | 94.3% | 92.7% | 96.7% | 96.7% | 94.4% | 98.0% | 95.8% | 96.7% | 96.6% | 90.3% | 95.5% | 94.5% | 95.9% | 96.1% | 97.9% | 88.4% | 96.5% | 95.3% | 95.4% | 97.2% | 93.5% | 101.4% | 93.3% | 97.6% | 92.5% | 96.5% | 94.3% | 92.8% | 98.7% | 92.8% | 97.7% | 93.7% | 96.1% | 96.6% | 95.4% | 98.4% | 95.0% | 97.2% |
| 2009-07-01 | 94.4% | 93.4% | 100.5% | 90.3% | 96.2% | 92.5% | 94.9% | 94.8% | 93.9% | 100.8% | 90.7% | 93.0% | 93.9% | 92.2% | 94.0% | 92.4% | 96.4% | 96.5% | 94.3% | 97.9% | 95.6% | 96.3% | 96.2% | 90.1% | 95.4% | 94.4% | 95.6% | 95.8% | 98.1% | 88.0% | 95.9% | 95.0% | 95.3% | 97.6% | 93.2% | 101.2% | 92.7% | 97.3% | 92.5% | 96.2% | 93.5% | 92.6% | 98.9% | 92.7% | 97.4% | 93.3% | 95.7% | 96.3% | 94.9% | 97.7% | 94.6% | 96.6% |
| 2009-08-01 | 94.3% | 93.1% | 100.5% | 89.9% | 96.1% | 92.2% | 94.7% | 94.7% | 93.7% | 100.9% | 90.4% | 92.7% | 93.7% | 92.0% | 93.7% | 92.9% | 96.5% | 96.2% | 94.2% | 97.9% | 95.4% | 96.2% | 96.2% | 90.2% | 95.1% | 94.1% | 95.6% | 95.7% | 97.8% | 87.6% | 95.9% | 94.9% | 95.3% | 97.4% | 93.0% | 101.2% | 92.5% | 97.1% | 92.1% | 96.1% | 93.5% | 92.5% | 98.5% | 92.6% | 97.2% | 93.1% | 96.1% | 96.3% | 94.8% | 97.7% | 94.4% | 96.2% |
| 2009-09-01 | 94.1% | 92.9% | 100.5% | 89.5% | 95.9% | 91.9% | 94.6% | 94.8% | 93.6% | 99.8% | 90.2% | 92.4% | 93.3% | 91.8% | 93.6% | 92.6% | 96.5% | 96.0% | 94.3% | 97.9% | 95.7% | 96.0% | 96.3% | 90.3% | 94.5% | 93.9% | 95.4% | 95.6% | 97.6% | 87.5% | 96.1% | 94.8% | 95.0% | 96.9% | 93.0% | 101.5% | 92.7% | 96.7% | 92.0% | 96.1% | 93.6% | 92.1% | 98.6% | 92.5% | 97.1% | 93.1% | 95.6% | 96.0% | 94.7% | 97.1% | 94.3% | 96.3% |
| 2009-10-01 | 94.0% | 92.7% | 100.7% | 89.2% | 95.6% | 92.2% | 94.4% | 94.5% | 93.7% | 100.4% | 90.1% | 92.3% | 93.3% | 92.2% | 93.5% | 92.6% | 96.2% | 95.7% | 94.3% | 97.5% | 95.6% | 96.0% | 96.2% | 90.4% | 94.9% | 93.5% | 95.1% | 95.7% | 97.5% | 87.0% | 96.0% | 94.5% | 94.6% | 96.7% | 92.5% | 101.5% | 92.5% | 96.4% | 91.8% | 96.1% | 93.6% | 92.1% | 98.3% | 92.5% | 97.0% | 92.9% | 95.8% | 96.0% | 94.6% | 97.1% | 94.4% | 95.7% |
| 2009-11-01 | 94.0% | 92.7% | 100.5% | 89.1% | 95.8% | 92.1% | 94.3% | 94.4% | 93.4% | 100.6% | 90.1% | 92.3% | 93.0% | 92.0% | 93.5% | 92.8% | 96.2% | 95.8% | 94.4% | 97.4% | 95.5% | 95.9% | 96.2% | 90.3% | 94.9% | 93.6% | 95.0% | 95.7% | 97.5% | 87.0% | 95.8% | 94.5% | 94.5% | 96.7% | 92.4% | 101.7% | 92.5% | 96.4% | 91.7% | 96.1% | 93.6% | 92.0% | 98.4% | 92.6% | 97.0% | 92.9% | 95.9% | 96.0% | 94.3% | 97.2% | 94.2% | 95.7% |
| 2009-12-01 | 93.8% | 92.7% | 100.4% | 88.9% | 95.7% | 91.9% | 94.1% | 94.4% | 93.0% | 100.7% | 89.9% | 92.2% | 92.9% | 91.9% | 93.3% | 92.7% | 96.0% | 95.4% | 94.1% | 97.1% | 95.5% | 95.8% | 96.4% | 90.3% | 94.9% | 93.5% | 95.0% | 95.5% | 97.1% | 87.1% | 96.0% | 94.5% | 94.4% | 96.7% | 92.3% | 101.8% | 92.4% | 96.2% | 91.6% | 96.0% | 93.6% | 91.8% | 98.1% | 92.4% | 97.0% | 92.8% | 95.7% | 95.9% | 94.2% | 97.4% | 94.2% | 95.5% |
| 2010-01-01 | 93.8% | 92.6% | 100.7% | 89.0% | 95.5% | 91.7% | 93.9% | 93.5% | 92.7% | 100.9% | 89.8% | 92.0% | 93.4% | 91.2% | 93.3% | 92.9% | 96.0% | 95.3% | 94.0% | 96.9% | 95.6% | 95.8% | 96.9% | 90.3% | 94.8% | 93.5% | 94.7% | 95.8% | 97.0% | 86.6% | 95.8% | 94.3% | 94.3% | 96.8% | 92.3% | 101.8% | 92.5% | 96.2% | 91.6% | 95.9% | 93.8% | 92.0% | 97.7% | 92.6% | 97.3% | 92.9% | 95.9% | 95.7% | 94.2% | 97.2% | 94.2% | 95.6% |
| 2010-02-01 | 93.7% | 92.4% | 100.5% | 88.9% | 95.3% | 91.6% | 94.1% | 93.5% | 92.1% | 100.3% | 89.9% | 91.9% | 93.1% | 91.5% | 93.4% | 92.9% | 96.0% | 95.3% | 93.6% | 96.8% | 95.5% | 94.6% | 96.7% | 90.2% | 94.7% | 93.5% | 94.7% | 95.4% | 97.1% | 86.4% | 95.6% | 94.0% | 94.4% | 96.8% | 92.1% | 102.2% | 92.4% | 96.1% | 91.5% | 95.7% | 93.7% | 92.0% | 97.8% | 92.4% | 97.3% | 92.7% | 95.8% | 95.2% | 94.2% | 97.1% | 94.2% | 95.7% |
| 2010-03-01 | 93.8% | 92.6% | 100.6% | 88.9% | 95.7% | 91.7% | 94.2% | 93.6% | 92.9% | 101.0% | 90.0% | 92.1% | 93.1% | 91.7% | 93.4% | 93.1% | 96.2% | 95.3% | 94.1% | 97.2% | 95.6% | 95.9% | 96.7% | 90.2% | 94.8% | 93.7% | 94.8% | 95.8% | 97.1% | 86.3% | 96.0% | 94.0% | 94.5% | 97.0% | 92.4% | 102.7% | 92.5% | 96.4% | 91.7% | 96.1% | 93.8% | 92.1% | 98.0% | 92.6% | 97.6% | 92.9% | 96.0% | 95.7% | 94.3% | 97.8% | 94.3% | 95.8% |
| 2010-04-01 | 94.0% | 92.8% | 101.1% | 89.0% | 96.0% | 92.3% | 94.3% | 94.2% | 93.4% | 101.8% | 90.2% | 92.2% | 93.3% | 91.9% | 93.6% | 93.4% | 96.5% | 95.8% | 94.5% | 97.3% | 95.7% | 96.4% | 96.9% | 90.6% | 95.2% | 94.1% | 94.8% | 95.8% | 97.4% | 86.5% | 96.0% | 94.4% | 94.7% | 97.4% | 92.6% | 103.6% | 92.8% | 96.7% | 91.9% | 96.5% | 93.8% | 92.7% | 98.4% | 93.0% | 97.8% | 93.2% | 96.9% | 96.3% | 94.5% | 97.8% | 94.6% | 96.4% |
| 2010-05-01 | 94.4% | 93.4% | 101.4% | 89.5% | 96.8% | 92.6% | 94.7% | 94.7% | 93.9% | 102.1% | 90.8% | 92.7% | 93.5% | 92.2% | 93.9% | 93.9% | 96.5% | 96.1% | 95.0% | 97.7% | 96.0% | 96.7% | 97.3% | 90.9% | 95.2% | 94.6% | 95.0% | 96.2% | 97.6% | 86.8% | 96.3% | 94.7% | 94.9% | 97.8% | 93.1% | 103.8% | 93.0% | 97.2% | 92.3% | 96.9% | 94.1% | 93.4% | 98.5% | 93.6% | 98.3% | 93.5% | 96.6% | 96.8% | 94.8% | 99.7% | 94.7% | 96.8% |
| 2010-06-01 | 94.3% | 93.3% | 101.9% | 89.1% | 97.3% | 92.5% | 94.6% | 94.4% | 94.0% | 102.3% | 90.6% | 92.7% | 93.3% | 91.7% | 93.8% | 93.6% | 96.3% | 96.3% | 95.1% | 98.0% | 95.3% | 96.8% | 96.9% | 91.0% | 95.2% | 94.7% | 94.8% | 95.9% | 97.9% | 86.7% | 96.0% | 94.6% | 95.2% | 97.7% | 93.0% | 103.5% | 93.0% | 97.3% | 92.5% | 97.0% | 93.9% | 93.1% | 98.8% | 93.4% | 98.4% | 93.5% | 96.4% | 96.8% | 94.7% | 98.6% | 94.7% | 96.6% |
| 2010-07-01 | 94.2% | 93.3% | 102.4% | 88.9% | 96.9% | 92.3% | 94.7% | 94.7% | 94.4% | 102.7% | 90.6% | 92.8% | 93.6% | 91.9% | 93.4% | 94.0% | 96.2% | 96.3% | 94.7% | 97.5% | 95.4% | 96.6% | 97.1% | 91.4% | 95.2% | 94.6% | 94.7% | 96.0% | 98.0% | 86.6% | 96.0% | 94.3% | 95.0% | 97.6% | 93.0% | 103.8% | 92.8% | 97.2% | 92.1% | 96.8% | 94.2% | 93.3% | 98.8% | 93.4% | 98.2% | 93.6% | 97.1% | 96.9% | 94.6% | 98.7% | 94.7% | 96.1% |
| 2010-08-01 | 94.2% | 93.1% | 102.2% | 88.8% | 96.9% | 92.3% | 94.6% | 94.8% | 94.5% | 101.3% | 90.6% | 92.7% | 93.4% | 91.9% | 93.9% | 93.6% | 96.2% | 96.3% | 94.6% | 97.5% | 95.1% | 96.6% | 97.1% | 91.0% | 95.3% | 94.2% | 95.4% | 96.0% | 98.0% | 86.6% | 96.0% | 94.1% | 94.5% | 97.4% | 93.0% | 104.1% | 92.8% | 97.1% | 92.4% | 97.0% | 94.4% | 93.3% | 99.0% | 93.4% | 98.4% | 93.6% | 96.7% | 96.8% | 94.6% | 98.6% | 94.8% | 96.5% |
| 2010-09-01 | 94.2% | 92.9% | 102.4% | 88.5% | 96.5% | 92.2% | 94.5% | 94.7% | 94.5% | 102.1% | 90.4% | 92.6% | 93.4% | 91.7% | 93.9% | 93.5% | 96.1% | 95.7% | 94.9% | 97.4% | 95.5% | 96.6% | 97.0% | 91.3% | 95.1% | 94.2% | 94.9% | 95.9% | 97.8% | 86.0% | 95.9% | 93.8% | 93.9% | 97.4% | 92.9% | 104.4% | 93.0% | 96.8% | 92.2% | 96.9% | 94.2% | 93.1% | 98.8% | 93.4% | 98.4% | 93.6% | 96.8% | 96.7% | 94.5% | 98.3% | 94.7% | 97.0% |
| 2010-10-01 | 94.4% | 93.2% | 102.7% | 89.0% | 96.5% | 92.6% | 94.8% | 95.0% | 94.2% | 102.4% | 90.7% | 92.9% | 93.8% | 92.3% | 94.2% | 93.9% | 96.6% | 96.3% | 95.3% | 97.5% | 95.6% | 96.9% | 97.5% | 91.6% | 95.7% | 94.5% | 95.1% | 95.9% | 97.9% | 86.3% | 96.2% | 94.0% | 94.2% | 97.7% | 93.3% | 105.5% | 93.4% | 97.4% | 92.7% | 97.2% | 94.0% | 93.3% | 99.2% | 93.6% | 98.9% | 93.9% | 97.5% | 96.9% | 95.0% | 98.6% | 95.1% | 97.2% |
| 2010-11-01 | 94.5% | 93.1% | 102.9% | 89.1% | 96.5% | 92.6% | 94.8% | 94.9% | 94.1% | 102.4% | 90.7% | 92.9% | 94.4% | 92.2% | 94.3% | 93.9% | 96.6% | 95.9% | 95.3% | 97.4% | 95.6% | 96.8% | 97.5% | 91.7% | 95.8% | 94.1% | 95.0% | 95.7% | 97.8% | 86.3% | 96.1% | 93.9% | 94.2% | 97.9% | 93.3% | 105.8% | 93.5% | 97.4% | 92.7% | 97.3% | 94.3% | 93.2% | 99.3% | 93.6% | 98.9% | 94.0% | 97.0% | 97.0% | 95.0% | 98.6% | 95.2% | 96.9% |
| 2010-12-01 | 94.5% | 93.0% | 102.8% | 89.4% | 96.6% | 92.7% | 95.0% | 95.0% | 94.4% | 102.5% | 90.8% | 92.9% | 93.9% | 92.0% | 94.3% | 93.9% | 96.7% | 96.1% | 95.5% | 97.6% | 95.6% | 96.9% | 97.6% | 91.7% | 95.8% | 94.3% | 94.9% | 95.8% | 97.9% | 86.4% | 96.3% | 94.0% | 94.3% | 97.9% | 93.3% | 106.3% | 93.6% | 97.6% | 92.6% | 97.4% | 94.2% | 93.5% | 99.1% | 93.6% | 99.1% | 94.2% | 96.7% | 97.0% | 95.1% | 98.4% | 95.1% | 96.8% |
| 2011-01-01 | 94.5% | 92.8% | 103.2% | 89.4% | 96.5% | 92.7% | 95.3% | 95.0% | 94.4% | 103.2% | 90.9% | 92.3% | 93.8% | 92.2% | 94.4% | 94.3% | 96.7% | 96.4% | 95.3% | 97.8% | 95.5% | 96.9% | 97.6% | 92.0% | 96.1% | 94.1% | 95.0% | 95.8% | 97.7% | 86.7% | 96.2% | 93.8% | 94.1% | 98.6% | 93.2% | 106.5% | 93.6% | 97.5% | 92.9% | 97.4% | 94.1% | 93.1% | 99.0% | 93.8% | 99.3% | 94.2% | 97.0% | 97.3% | 95.3% | 98.2% | 95.3% | 96.8% |
| 2011-02-01 | 94.7% | 92.9% | 102.8% | 89.5% | 96.2% | 92.8% | 95.1% | 95.2% | 94.7% | 103.3% | 90.9% | 93.1% | 94.3% | 92.2% | 94.4% | 94.4% | 96.8% | 96.1% | 95.5% | 98.0% | 95.8% | 97.1% | 97.7% | 92.0% | 96.2% | 94.0% | 94.9% | 95.9% | 97.7% | 86.7% | 96.3% | 93.9% | 94.3% | 98.6% | 93.7% | 106.9% | 93.8% | 97.0% | 93.0% | 97.5% | 94.2% | 93.5% | 99.1% | 94.1% | 99.3% | 94.5% | 96.9% | 97.5% | 95.3% | 98.6% | 95.3% | 97.0% |
| 2011-03-01 | 94.9% | 93.0% | 102.8% | 89.6% | 96.4% | 92.8% | 95.4% | 95.1% | 94.7% | 103.4% | 91.0% | 93.3% | 94.5% | 92.1% | 94.6% | 94.7% | 97.0% | 96.1% | 95.7% | 98.1% | 95.7% | 97.2% | 97.8% | 92.4% | 96.3% | 94.2% | 95.1% | 96.1% | 97.9% | 86.7% | 96.4% | 93.9% | 94.4% | 98.7% | 93.7% | 107.5% | 93.9% | 97.7% | 93.1% | 97.6% | 94.3% | 93.7% | 99.2% | 94.2% | 99.7% | 94.7% | 97.1% | 97.5% | 95.3% | 98.7% | 95.4% | 97.2% |
| 2011-04-01 | 95.1% | 93.0% | 102.9% | 89.7% | 97.2% | 93.0% | 95.8% | 95.7% | 95.3% | 103.8% | 91.4% | 93.5% | 94.3% | 92.6% | 94.8% | 94.9% | 97.3% | 96.6% | 95.8% | 98.2% | 95.6% | 97.3% | 98.0% | 92.7% | 96.6% | 94.2% | 95.3% | 96.2% | 98.3% | 86.9% | 96.7% | 94.1% | 94.5% | 99.0% | 93.9% | 107.9% | 94.0% | 98.2% | 93.1% | 97.9% | 94.6% | 94.1% | 99.3% | 94.6% | 100.1% | 95.0% | 97.0% | 97.6% | 95.7% | 99.1% | 95.5% | 97.4% |
| 2011-05-01 | 95.2% | 92.9% | 102.8% | 90.0% | 96.6% | 93.0% | 95.8% | 95.4% | 94.5% | 103.5% | 91.3% | 93.5% | 94.2% | 92.6% | 94.7% | 95.1% | 97.2% | 96.6% | 95.6% | 98.2% | 95.3% | 97.2% | 98.0% | 92.7% | 96.8% | 94.2% | 95.3% | 96.4% | 98.2% | 87.0% | 96.5% | 94.0% | 94.5% | 98.8% | 93.9% | 108.3% | 93.9% | 98.1% | 93.0% | 97.8% | 94.5% | 94.0% | 99.5% | 94.7% | 100.1% | 95.0% | 97.4% | 97.5% | 95.7% | 99.1% | 95.5% | 97.7% |
| 2011-06-01 | 95.3% | 92.7% | 103.3% | 89.6% | 96.4% | 93.0% | 95.8% | 95.2% | 94.4% | 103.8% | 91.2% | 93.5% | 94.1% | 92.6% | 94.8% | 94.8% | 97.2% | 96.1% | 95.8% | 97.9% | 95.4% | 97.2% | 97.8% | 92.9% | 96.8% | 94.3% | 95.2% | 96.3% | 98.4% | 86.9% | 96.4% | 93.9% | 94.6% | 98.9% | 94.1% | 108.6% | 93.8% | 98.2% | 93.1% | 98.0% | 94.6% | 94.0% | 100.0% | 94.7% | 100.3% | 95.2% | 97.2% | 97.4% | 95.7% | 98.7% | 95.5% | 97.9% |
| 2011-07-01 | 95.4% | 93.0% | 103.5% | 89.6% | 97.1% | 93.3% | 96.1% | 95.6% | 94.5% | 104.2% | 91.5% | 93.7% | 94.8% | 93.2% | 95.0% | 95.3% | 97.4% | 96.9% | 95.9% | 98.4% | 96.0% | 97.6% | 98.5% | 93.4% | 96.2% | 94.4% | 95.4% | 96.2% | 98.5% | 87.2% | 96.4% | 94.2% | 94.8% | 99.1% | 94.1% | 109.6% | 94.5% | 98.6% | 93.3% | 97.8% | 94.7% | 94.2% | 99.8% | 95.1% | 100.6% | 95.7% | 97.3% | 97.7% | 96.0% | 99.1% | 95.9% | 98.2% |
| 2011-08-01 | 95.5% | 93.1% | 103.4% | 90.2% | 97.1% | 93.4% | 96.3% | 95.5% | 94.2% | 103.9% | 91.6% | 93.7% | 94.5% | 93.3% | 95.2% | 94.9% | 97.6% | 97.0% | 96.3% | 98.4% | 95.9% | 97.4% | 98.4% | 93.4% | 97.2% | 94.2% | 95.3% | 96.7% | 98.5% | 87.2% | 96.3% | 94.1% | 94.4% | 99.1% | 94.2% | 110.3% | 94.6% | 98.3% | 93.3% | 97.8% | 94.5% | 94.3% | 99.8% | 95.3% | 100.8% | 95.9% | 97.8% | 97.6% | 96.1% | 99.3% | 95.8% | 98.8% |
| 2011-09-01 | 95.6% | 93.3% | 104.1% | 90.4% | 97.1% | 93.6% | 96.7% | 95.7% | 94.6% | 104.5% | 91.8% | 93.9% | 95.0% | 93.4% | 95.2% | 95.6% | 97.9% | 96.7% | 96.5% | 98.6% | 96.1% | 97.5% | 98.7% | 93.7% | 97.6% | 94.3% | 95.5% | 97.1% | 98.8% | 87.3% | 96.6% | 94.3% | 94.4% | 99.4% | 94.3% | 111.4% | 94.6% | 99.1% | 93.5% | 98.0% | 94.6% | 94.3% | 100.1% | 95.3% | 101.0% | 96.1% | 97.8% | 98.2% | 96.2% | 99.9% | 95.9% | 98.9% |
| 2011-10-01 | 95.8% | 93.1% | 104.3% | 90.4% | 97.5% | 93.6% | 96.6% | 95.5% | 94.2% | 104.0% | 91.8% | 93.7% | 95.1% | 93.5% | 95.2% | 95.7% | 97.8% | 96.9% | 96.4% | 98.6% | 96.0% | 97.7% | 98.6% | 93.8% | 97.4% | 94.4% | 95.3% | 97.1% | 98.9% | 87.4% | 96.6% | 94.4% | 94.0% | 99.4% | 94.3% | 111.9% | 94.6% | 99.0% | 93.4% | 98.0% | 94.7% | 94.3% | 100.4% | 95.5% | 100.9% | 96.2% | 97.9% | 98.1% | 96.2% | 100.1% | 95.7% | 98.9% |
| 2011-11-01 | 95.9% | 93.2% | 104.2% | 90.6% | 97.5% | 93.8% | 96.8% | 95.5% | 94.3% | 103.8% | 91.9% | 93.8% | 95.2% | 93.9% | 95.3% | 95.6% | 98.0% | 97.0% | 96.6% | 98.6% | 96.1% | 97.6% | 98.7% | 94.0% | 97.5% | 94.3% | 95.4% | 97.3% | 99.1% | 87.4% | 96.9% | 94.4% | 94.0% | 99.5% | 94.4% | 112.8% | 94.9% | 99.0% | 93.6% | 98.1% | 94.7% | 94.3% | 100.4% | 95.6% | 101.1% | 96.3% | 97.9% | 98.2% | 96.3% | 100.3% | 95.8% | 99.1% |
| 2011-12-01 | 96.0% | 93.1% | 104.0% | 90.7% | 97.4% | 93.9% | 97.0% | 95.7% | 94.4% | 104.1% | 92.0% | 93.8% | 95.4% | 94.1% | 95.3% | 95.9% | 98.1% | 96.9% | 96.6% | 98.7% | 95.9% | 97.8% | 98.8% | 94.0% | 97.7% | 94.3% | 95.5% | 97.5% | 99.2% | 87.4% | 96.8% | 94.5% | 94.1% | 99.8% | 94.5% | 113.8% | 95.0% | 99.2% | 93.7% | 98.2% | 94.8% | 94.5% | 100.8% | 95.7% | 101.4% | 96.7% | 98.2% | 98.2% | 96.3% | 100.6% | 95.9% | 99.3% |
| 2012-01-01 | 96.3% | 93.4% | 104.3% | 91.0% | 97.5% | 94.2% | 97.2% | 95.9% | 94.4% | 104.2% | 92.3% | 94.0% | 94.1% | 93.7% | 95.6% | 96.3% | 98.3% | 97.6% | 97.0% | 99.0% | 95.9% | 98.2% | 99.2% | 94.3% | 97.7% | 94.7% | 95.7% | 97.9% | 99.4% | 87.7% | 97.1% | 94.8% | 93.8% | 100.1% | 95.0% | 115.4% | 95.4% | 99.5% | 93.9% | 98.3% | 95.0% | 95.0% | 100.8% | 96.0% | 101.8% | 97.0% | 98.3% | 98.5% | 96.4% | 100.7% | 95.7% | 99.3% |
| 2012-02-01 | 96.5% | 93.4% | 104.8% | 91.1% | 97.5% | 94.4% | 97.3% | 96.2% | 94.6% | 104.2% | 92.4% | 94.1% | 95.7% | 93.8% | 95.7% | 96.6% | 98.4% | 97.6% | 97.1% | 99.1% | 96.3% | 98.3% | 99.3% | 94.4% | 97.8% | 94.8% | 95.7% | 97.7% | 99.5% | 87.8% | 96.9% | 95.0% | 94.2% | 100.3% | 95.1% | 116.2% | 95.6% | 99.9% | 94.0% | 98.5% | 95.4% | 95.1% | 100.8% | 96.2% | 102.0% | 97.3% | 98.5% | 98.7% | 96.5% | 100.9% | 96.1% | 99.4% |
| 2012-03-01 | 96.6% | 93.7% | 105.0% | 91.4% | 97.7% | 94.7% | 97.6% | 96.4% | 94.9% | 104.4% | 92.7% | 94.4% | 95.6% | 93.9% | 96.0% | 96.8% | 98.8% | 97.9% | 97.4% | 99.3% | 96.4% | 98.5% | 99.6% | 94.7% | 98.1% | 95.0% | 95.9% | 97.8% | 99.9% | 87.9% | 97.3% | 95.3% | 94.5% | 100.5% | 95.3% | 117.1% | 96.0% | 100.1% | 94.0% | 98.9% | 95.6% | 95.4% | 101.2% | 96.6% | 102.4% | 97.7% | 98.8% | 98.8% | 96.8% | 101.1% | 96.6% | 99.4% |
| 2012-04-01 | 96.7% | 93.8% | 104.8% | 91.4% | 97.7% | 94.8% | 97.8% | 95.9% | 94.7% | 104.2% | 93.0% | 94.5% | 96.2% | 94.1% | 96.0% | 96.7% | 98.8% | 97.7% | 97.3% | 99.8% | 96.5% | 98.3% | 99.3% | 95.0% | 98.4% | 94.9% | 95.6% | 98.2% | 99.9% | 88.1% | 97.2% | 94.8% | 94.3% | 100.4% | 95.4% | 117.9% | 95.9% | 100.4% | 94.1% | 98.6% | 95.4% | 95.4% | 101.7% | 96.6% | 102.6% | 98.3% | 98.3% | 98.6% | 97.0% | 101.0% | 96.7% | 99.9% |
| 2012-05-01 | 96.8% | 93.6% | 104.9% | 91.5% | 97.7% | 95.1% | 98.0% | 96.0% | 94.9% | 104.7% | 93.0% | 94.7% | 96.4% | 94.3% | 96.0% | 96.8% | 98.8% | 97.9% | 97.5% | 99.9% | 96.6% | 98.3% | 99.4% | 94.8% | 98.1% | 94.9% | 95.7% | 98.6% | 100.0% | 88.3% | 97.2% | 95.0% | 94.3% | 100.5% | 95.6% | 118.4% | 96.0% | 100.5% | 94.2% | 98.6% | 95.5% | 95.4% | 101.4% | 96.7% | 102.9% | 98.8% | 98.8% | 98.5% | 97.2% | 102.2% | 96.8% | 99.5% |
| 2012-06-01 | 96.8% | 93.7% | 105.1% | 91.9% | 97.7% | 95.4% | 98.3% | 96.1% | 94.8% | 104.4% | 93.2% | 94.8% | 96.6% | 94.5% | 96.1% | 97.0% | 98.8% | 98.1% | 97.6% | 99.7% | 96.5% | 98.4% | 99.8% | 94.9% | 98.3% | 94.9% | 95.7% | 98.6% | 100.2% | 88.6% | 97.5% | 95.2% | 94.7% | 100.6% | 95.4% | 119.3% | 96.1% | 100.6% | 94.3% | 98.5% | 95.5% | 95.6% | 101.6% | 96.9% | 103.2% | 99.0% | 98.6% | 98.6% | 97.4% | 100.1% | 96.7% | 99.1% |
| 2012-07-01 | 96.9% | 93.6% | 104.9% | 91.6% | 97.4% | 95.5% | 98.4% | 96.1% | 95.0% | 104.3% | 93.3% | 94.7% | 96.8% | 94.7% | 96.1% | 96.8% | 99.0% | 97.6% | 97.5% | 99.4% | 96.4% | 98.5% | 99.8% | 95.1% | 98.0% | 95.0% | 95.9% | 98.7% | 100.2% | 88.5% | 97.5% | 95.0% | 94.5% | 100.2% | 95.5% | 118.9% | 96.0% | 100.5% | 94.5% | 98.4% | 95.2% | 95.6% | 101.4% | 96.8% | 103.4% | 98.8% | 98.8% | 98.4% | 97.5% | 100.1% | 96.5% | 98.9% |
| 2012-08-01 | 97.1% | 93.8% | 104.8% | 92.1% | 97.5% | 95.6% | 98.6% | 96.2% | 95.2% | 104.6% | 93.4% | 94.8% | 97.7% | 94.9% | 96.2% | 97.0% | 99.0% | 97.9% | 97.4% | 99.4% | 96.3% | 98.5% | 99.9% | 95.1% | 98.4% | 95.2% | 95.9% | 98.9% | 100.2% | 88.7% | 97.7% | 95.2% | 94.3% | 100.6% | 95.8% | 119.3% | 96.0% | 100.6% | 94.7% | 98.4% | 95.7% | 95.8% | 101.4% | 96.9% | 103.7% | 99.1% | 98.9% | 98.7% | 97.6% | 100.0% | 96.6% | 99.1% |
| 2012-09-01 | 97.2% | 93.9% | 105.0% | 92.4% | 97.4% | 95.8% | 98.8% | 96.4% | 95.1% | 105.1% | 93.6% | 94.9% | 97.1% | 95.3% | 96.4% | 97.4% | 99.2% | 97.8% | 97.6% | 99.4% | 96.4% | 98.8% | 100.1% | 95.3% | 98.9% | 95.1% | 96.0% | 99.3% | 100.3% | 88.9% | 98.1% | 95.4% | 94.6% | 101.0% | 96.0% | 119.9% | 96.1% | 100.7% | 94.7% | 98.6% | 96.0% | 95.9% | 101.7% | 97.1% | 104.0% | 99.4% | 99.0% | 99.1% | 97.8% | 100.6% | 96.8% | 99.2% |
| 2012-10-01 | 97.3% | 94.1% | 106.5% | 92.4% | 97.4% | 96.0% | 99.3% | 96.5% | 95.5% | 105.5% | 93.9% | 95.2% | 97.3% | 95.6% | 96.4% | 97.4% | 99.2% | 98.1% | 97.7% | 99.7% | 96.3% | 98.9% | 100.1% | 95.3% | 98.9% | 95.1% | 96.1% | 99.1% | 100.4% | 89.2% | 97.8% | 95.5% | 95.5% | 101.0% | 96.1% | 120.0% | 96.3% | 101.3% | 94.9% | 98.6% | 95.7% | 96.0% | 101.7% | 97.2% | 104.3% | 99.7% | 98.6% | 99.4% | 98.2% | 100.5% | 96.9% | 99.2% |
| 2012-11-01 | 97.4% | 94.1% | 105.7% | 92.6% | 97.4% | 96.2% | 99.5% | 96.5% | 95.7% | 105.5% | 94.1% | 95.4% | 98.1% | 95.8% | 96.5% | 97.4% | 99.3% | 98.1% | 97.8% | 99.9% | 96.4% | 98.8% | 100.2% | 95.5% | 99.2% | 95.2% | 96.3% | 99.1% | 100.5% | 89.4% | 97.9% | 95.1% | 95.4% | 100.7% | 96.4% | 119.6% | 96.3% | 101.3% | 94.9% | 98.6% | 95.7% | 96.4% | 101.8% | 97.3% | 104.6% | 100.2% | 98.8% | 99.4% | 98.3% | 100.2% | 97.2% | 99.3% |
| 2012-12-01 | 97.6% | 94.1% | 105.6% | 92.8% | 97.7% | 96.5% | 99.6% | 96.7% | 95.9% | 105.6% | 94.2% | 95.5% | 97.6% | 95.9% | 96.5% | 97.4% | 99.4% | 98.2% | 97.8% | 100.0% | 96.3% | 99.0% | 100.3% | 95.8% | 99.3% | 95.3% | 96.4% | 99.4% | 100.7% | 89.3% | 97.8% | 95.5% | 95.2% | 101.2% | 96.5% | 120.5% | 96.4% | 101.5% | 95.1% | 98.6% | 96.1% | 96.5% | 101.9% | 97.4% | 104.8% | 100.3% | 99.0% | 99.5% | 98.4% | 100.3% | 97.1% | 99.4% |
| 2013-01-01 | 97.7% | 94.2% | 105.0% | 92.9% | 97.6% | 96.6% | 99.8% | 96.6% | 95.8% | 105.6% | 94.3% | 95.8% | 96.6% | 96.0% | 96.7% | 97.5% | 99.4% | 98.3% | 98.0% | 100.2% | 96.5% | 99.3% | 100.6% | 96.1% | 99.6% | 95.3% | 96.5% | 99.7% | 100.6% | 89.6% | 98.0% | 95.9% | 95.3% | 101.3% | 96.6% | 120.7% | 96.6% | 101.1% | 95.3% | 98.6% | 96.3% | 96.6% | 102.0% | 97.5% | 104.8% | 100.6% | 99.1% | 99.6% | 98.6% | 100.5% | 96.8% | 99.5% |
| 2013-02-01 | 97.9% | 94.4% | 105.6% | 93.2% | 97.8% | 96.9% | 100.2% | 96.5% | 96.3% | 105.7% | 94.6% | 96.0% | 98.1% | 96.3% | 96.9% | 97.9% | 99.6% | 98.5% | 98.1% | 100.5% | 96.5% | 99.3% | 100.8% | 96.4% | 99.9% | 95.6% | 96.7% | 100.1% | 100.8% | 89.7% | 98.1% | 96.0% | 95.4% | 101.5% | 96.8% | 121.4% | 96.7% | 101.4% | 95.5% | 98.8% | 96.1% | 96.7% | 102.1% | 97.8% | 105.4% | 100.9% | 99.1% | 99.8% | 98.9% | 100.6% | 97.4% | 99.3% |
| 2013-03-01 | 98.0% | 94.5% | 105.6% | 93.4% | 97.7% | 97.1% | 100.5% | 96.8% | 96.5% | 105.7% | 94.8% | 96.1% | 98.2% | 96.5% | 96.8% | 97.9% | 99.6% | 98.5% | 98.2% | 100.6% | 96.6% | 99.4% | 101.0% | 96.5% | 100.0% | 95.7% | 96.6% | 100.2% | 100.7% | 90.0% | 97.9% | 96.2% | 95.3% | 101.7% | 97.0% | 121.9% | 96.8% | 101.5% | 95.7% | 98.9% | 96.5% | 96.7% | 102.1% | 97.8% | 105.7% | 101.2% | 99.4% | 99.8% | 98.9% | 100.6% | 97.4% | 99.5% |
| 2013-04-01 | 98.2% | 94.6% | 105.6% | 93.6% | 97.7% | 97.4% | 100.6% | 96.9% | 96.6% | 106.3% | 95.0% | 96.2% | 98.1% | 96.6% | 96.7% | 97.8% | 99.4% | 98.7% | 98.2% | 100.8% | 96.7% | 99.3% | 101.2% | 96.2% | 99.4% | 95.6% | 96.6% | 100.4% | 100.7% | 90.3% | 98.1% | 95.9% | 95.6% | 102.0% | 97.1% | 121.1% | 97.0% | 101.6% | 96.0% | 98.7% | 96.3% | 97.0% | 101.5% | 98.1% | 105.8% | 101.5% | 99.6% | 99.5% | 99.1% | 100.4% | 97.0% | 99.6% |
| 2013-05-01 | 98.3% | 94.7% | 105.1% | 93.8% | 97.5% | 97.6% | 100.9% | 96.9% | 96.7% | 106.2% | 95.2% | 96.3% | 98.6% | 97.0% | 96.8% | 97.5% | 99.9% | 98.6% | 98.2% | 100.7% | 96.9% | 99.3% | 101.3% | 96.6% | 100.0% | 95.6% | 96.7% | 100.5% | 101.1% | 90.4% | 98.3% | 96.0% | 95.7% | 101.9% | 97.1% | 122.4% | 97.2% | 101.8% | 96.1% | 98.7% | 96.4% | 97.1% | 102.3% | 98.2% | 106.0% | 101.6% | 99.2% | 99.4% | 99.3% | 100.5% | 97.4% | 99.7% |
| 2013-06-01 | 98.5% | 94.7% | 105.5% | 93.9% | 97.3% | 97.7% | 101.2% | 97.2% | 96.8% | 106.0% | 95.5% | 96.4% | 98.6% | 97.0% | 96.9% | 97.9% | 100.1% | 98.7% | 98.3% | 100.9% | 97.0% | 99.5% | 101.5% | 96.7% | 100.1% | 95.8% | 96.8% | 100.4% | 101.1% | 91.0% | 98.1% | 96.2% | 95.2% | 102.0% | 97.0% | 122.9% | 97.2% | 101.9% | 96.3% | 98.7% | 96.9% | 97.4% | 102.2% | 98.3% | 106.3% | 101.7% | 99.4% | 99.4% | 99.4% | 100.3% | 97.6% | 100.0% |
| 2013-07-01 | 98.6% | 94.7% | 105.3% | 94.0% | 97.5% | 97.9% | 101.4% | 97.5% | 97.1% | 106.1% | 95.7% | 96.6% | 99.0% | 97.0% | 97.0% | 97.7% | 100.6% | 98.9% | 98.4% | 100.9% | 97.1% | 99.6% | 101.4% | 96.5% | 99.7% | 95.6% | 96.8% | 100.2% | 101.3% | 91.0% | 98.1% | 96.2% | 95.3% | 102.0% | 97.2% | 123.2% | 97.2% | 102.0% | 96.4% | 98.7% | 96.8% | 97.6% | 102.3% | 98.3% | 106.6% | 102.1% | 98.9% | 99.4% | 99.5% | 100.3% | 97.6% | 99.9% |
| 2013-08-01 | 98.7% | 94.8% | 105.6% | 94.2% | 97.4% | 98.2% | 101.7% | 97.2% | 97.6% | 106.4% | 96.0% | 96.8% | 98.6% | 97.2% | 97.2% | 98.4% | 100.7% | 99.0% | 98.6% | 101.0% | 97.1% | 99.5% | 101.6% | 97.0% | 100.2% | 95.8% | 96.9% | 100.5% | 101.5% | 91.3% | 98.4% | 96.5% | 95.4% | 102.2% | 97.5% | 123.6% | 97.3% | 102.1% | 96.7% | 98.8% | 97.1% | 97.8% | 102.4% | 98.5% | 106.8% | 102.2% | 99.4% | 99.5% | 99.8% | 100.3% | 97.8% | 99.9% |
| 2013-09-01 | 98.9% | 94.7% | 105.8% | 94.5% | 97.6% | 98.3% | 102.0% | 97.1% | 97.6% | 107.0% | 96.2% | 97.0% | 99.0% | 97.2% | 97.2% | 98.4% | 100.8% | 99.3% | 98.9% | 101.3% | 97.3% | 99.6% | 101.7% | 97.2% | 100.7% | 96.1% | 97.1% | 100.7% | 101.6% | 91.2% | 98.2% | 96.5% | 95.4% | 102.7% | 97.8% | 123.9% | 97.4% | 102.3% | 97.1% | 98.9% | 97.1% | 98.1% | 102.5% | 98.7% | 107.1% | 102.3% | 99.2% | 99.6% | 100.0% | 100.1% | 98.1% | 99.6% |
| 2013-10-01 | 99.0% | 94.8% | 105.5% | 94.6% | 97.7% | 98.5% | 102.2% | 97.1% | 97.9% | 106.5% | 96.4% | 97.3% | 99.4% | 98.0% | 97.2% | 98.6% | 100.5% | 99.4% | 98.9% | 101.4% | 97.4% | 99.5% | 101.8% | 97.4% | 100.8% | 96.0% | 97.2% | 101.0% | 101.8% | 91.4% | 98.7% | 96.5% | 95.5% | 102.8% | 98.0% | 124.0% | 97.6% | 102.3% | 97.2% | 98.9% | 97.4% | 98.4% | 102.7% | 99.0% | 107.3% | 102.8% | 99.6% | 99.5% | 100.4% | 100.1% | 98.1% | 99.7% |
| 2013-11-01 | 99.2% | 94.9% | 105.7% | 94.9% | 97.8% | 98.9% | 102.4% | 97.2% | 98.2% | 106.9% | 96.6% | 97.4% | 99.2% | 98.1% | 97.3% | 99.1% | 100.8% | 99.5% | 99.0% | 101.6% | 97.1% | 99.7% | 101.9% | 97.5% | 100.8% | 96.2% | 97.2% | 101.0% | 102.0% | 91.8% | 98.8% | 96.7% | 95.5% | 103.0% | 98.1% | 124.9% | 97.7% | 102.4% | 97.5% | 98.9% | 97.4% | 98.4% | 103.0% | 99.4% | 107.6% | 103.1% | 99.8% | 99.7% | 100.5% | 100.1% | 98.1% | 99.6% |
| 2013-12-01 | 99.3% | 95.1% | 105.8% | 95.0% | 97.5% | 99.1% | 102.7% | 97.0% | 97.9% | 106.9% | 96.9% | 97.6% | 99.6% | 98.2% | 97.5% | 99.1% | 100.8% | 99.6% | 99.1% | 101.3% | 97.2% | 99.5% | 102.1% | 97.6% | 100.9% | 96.2% | 97.2% | 101.1% | 102.1% | 91.9% | 99.0% | 96.5% | 95.7% | 103.0% | 98.3% | 124.3% | 97.8% | 102.2% | 97.7% | 98.9% | 97.1% | 98.7% | 103.0% | 99.5% | 107.7% | 103.4% | 99.9% | 99.6% | 100.7% | 100.0% | 98.3% | 99.9% |
| 2014-01-01 | 99.4% | 95.0% | 105.8% | 95.1% | 97.8% | 99.4% | 103.1% | 97.3% | 98.4% | 105.9% | 97.1% | 97.8% | 99.4% | 98.6% | 97.7% | 98.3% | 100.7% | 99.5% | 99.1% | 101.6% | 97.0% | 99.6% | 102.3% | 97.6% | 100.8% | 96.4% | 97.0% | 101.1% | 102.2% | 92.3% | 99.0% | 96.4% | 95.9% | 102.9% | 98.3% | 124.8% | 97.7% | 102.4% | 98.0% | 99.0% | 97.3% | 98.9% | 103.4% | 99.5% | 107.9% | 103.5% | 99.9% | 99.6% | 101.1% | 99.8% | 98.4% | 100.2% |
| 2014-02-01 | 99.5% | 94.9% | 105.7% | 95.1% | 98.0% | 99.6% | 103.3% | 97.1% | 98.3% | 106.1% | 97.3% | 97.7% | 99.3% | 98.9% | 97.7% | 98.8% | 100.9% | 99.8% | 99.1% | 101.7% | 97.2% | 99.6% | 102.6% | 97.9% | 100.9% | 96.1% | 97.3% | 101.3% | 102.4% | 92.7% | 99.0% | 96.4% | 95.8% | 103.2% | 98.0% | 125.4% | 97.9% | 102.5% | 97.9% | 98.9% | 97.7% | 98.7% | 103.4% | 99.6% | 108.2% | 103.7% | 99.9% | 99.5% | 101.1% | 99.7% | 98.4% | 100.3% |
| 2014-03-01 | 99.7% | 95.1% | 105.9% | 95.2% | 98.1% | 99.8% | 103.6% | 97.3% | 98.5% | 106.2% | 97.6% | 98.4% | 99.5% | 99.1% | 97.8% | 99.0% | 101.0% | 100.0% | 99.3% | 101.9% | 97.2% | 99.7% | 102.7% | 98.0% | 100.9% | 96.2% | 97.3% | 101.0% | 102.3% | 93.0% | 99.0% | 96.4% | 95.7% | 103.4% | 98.6% | 125.8% | 98.0% | 102.6% | 98.3% | 99.1% | 97.6% | 99.4% | 103.3% | 99.9% | 108.5% | 103.9% | 100.2% | 99.6% | 101.3% | 99.8% | 98.5% | 100.4% |
| 2014-04-01 | 99.9% | 95.4% | 106.2% | 95.5% | 98.3% | 100.1% | 104.1% | 97.6% | 98.7% | 106.6% | 98.0% | 98.7% | 99.5% | 99.4% | 98.0% | 99.3% | 101.2% | 100.2% | 99.7% | 102.0% | 97.1% | 100.0% | 103.0% | 97.8% | 101.0% | 96.4% | 97.8% | 101.4% | 102.4% | 93.4% | 99.2% | 97.0% | 96.0% | 103.7% | 99.1% | 126.3% | 98.3% | 102.8% | 98.6% | 99.4% | 98.0% | 99.7% | 103.6% | 100.1% | 109.0% | 104.2% | 99.8% | 100.1% | 101.3% | 100.1% | 98.6% | 100.7% |
| 2014-05-01 | 100.1% | 95.4% | 106.1% | 95.5% | 98.5% | 100.3% | 104.4% | 97.6% | 99.1% | 106.3% | 98.3% | 99.0% | 99.9% | 99.3% | 98.2% | 99.6% | 101.5% | 100.3% | 99.8% | 102.3% | 97.4% | 100.2% | 103.1% | 98.3% | 101.5% | 96.4% | 97.9% | 101.4% | 102.5% | 93.7% | 98.9% | 97.2% | 96.4% | 103.9% | 99.3% | 127.0% | 98.4% | 102.9% | 98.8% | 99.6% | 98.3% | 99.9% | 103.7% | 100.2% | 109.3% | 104.3% | 100.3% | 100.3% | 101.4% | 101.5% | 98.9% | 101.3% |
| 2014-06-01 | 100.3% | 95.6% | 105.7% | 95.8% | 98.5% | 100.5% | 104.7% | 97.7% | 99.2% | 107.1% | 98.5% | 99.2% | 99.8% | 99.5% | 98.2% | 99.7% | 101.4% | 100.3% | 99.9% | 102.3% | 97.8% | 100.4% | 103.2% | 98.8% | 101.7% | 96.5% | 97.9% | 101.5% | 102.4% | 93.8% | 99.4% | 97.1% | 96.0% | 104.1% | 99.3% | 127.5% | 98.6% | 103.1% | 99.1% | 99.7% | 98.2% | 100.0% | 103.8% | 100.3% | 109.6% | 104.6% | 100.5% | 100.3% | 101.7% | 98.8% | 99.1% | 101.7% |
| 2014-07-01 | 100.5% | 95.6% | 106.1% | 95.9% | 98.5% | 100.5% | 104.9% | 97.8% | 99.1% | 107.1% | 98.7% | 99.6% | 99.9% | 99.6% | 98.3% | 99.5% | 101.4% | 100.4% | 100.2% | 102.6% | 97.5% | 100.2% | 103.4% | 98.6% | 101.8% | 96.6% | 97.9% | 101.8% | 102.4% | 94.0% | 99.6% | 97.2% | 96.5% | 104.2% | 99.5% | 128.5% | 98.5% | 103.3% | 99.2% | 99.6% | 98.3% | 100.0% | 104.1% | 100.6% | 109.9% | 104.7% | 100.3% | 100.2% | 102.1% | 99.3% | 99.1% | 101.8% |
| 2014-08-01 | 100.6% | 95.8% | 105.9% | 96.0% | 98.7% | 100.9% | 105.3% | 97.9% | 99.5% | 107.2% | 99.1% | 99.9% | 100.3% | 99.8% | 98.4% | 99.7% | 101.6% | 100.4% | 100.4% | 102.8% | 97.6% | 100.6% | 103.3% | 98.7% | 101.9% | 96.6% | 98.1% | 101.8% | 102.6% | 94.5% | 98.6% | 97.2% | 96.6% | 104.5% | 99.6% | 128.5% | 98.8% | 103.4% | 99.4% | 99.8% | 98.5% | 100.3% | 104.2% | 100.9% | 110.1% | 105.2% | 100.7% | 100.2% | 102.4% | 99.6% | 99.6% | 101.4% |
| 2014-09-01 | 100.8% | 96.0% | 105.8% | 96.2% | 99.0% | 101.2% | 105.6% | 97.9% | 99.6% | 107.6% | 99.4% | 100.1% | 100.3% | 99.7% | 98.4% | 99.7% | 101.9% | 100.5% | 100.4% | 103.1% | 97.7% | 100.7% | 103.9% | 98.6% | 101.9% | 96.7% | 98.1% | 101.9% | 102.7% | 94.9% | 99.8% | 97.3% | 96.7% | 104.6% | 99.9% | 128.6% | 99.0% | 103.5% | 99.8% | 99.8% | 98.7% | 100.7% | 104.3% | 101.1% | 110.5% | 105.6% | 100.5% | 100.4% | 102.7% | 100.2% | 99.6% | 101.6% |
| 2014-10-01 | 101.0% | 96.1% | 106.1% | 96.5% | 99.1% | 101.4% | 106.0% | 97.9% | 99.8% | 107.7% | 99.6% | 100.2% | 100.4% | 100.1% | 98.6% | 100.0% | 101.6% | 100.5% | 100.5% | 103.1% | 97.9% | 100.7% | 104.1% | 98.9% | 102.0% | 96.8% | 98.4% | 101.6% | 102.8% | 95.1% | 99.8% | 97.3% | 97.0% | 104.6% | 100.1% | 129.1% | 99.2% | 103.7% | 100.1% | 100.0% | 98.6% | 101.0% | 104.3% | 101.3% | 110.9% | 105.9% | 100.4% | 100.3% | 102.7% | 100.4% | 99.6% | 101.8% |
| 2014-11-01 | 101.2% | 96.2% | 106.3% | 96.8% | 99.3% | 101.7% | 106.2% | 98.1% | 100.6% | 107.8% | 100.0% | 100.5% | 101.0% | 100.3% | 98.8% | 100.4% | 101.8% | 100.7% | 100.7% | 103.4% | 97.7% | 100.9% | 104.5% | 99.1% | 102.2% | 97.1% | 98.5% | 101.5% | 102.9% | 95.3% | 99.9% | 97.4% | 97.1% | 104.8% | 100.4% | 129.4% | 99.4% | 103.9% | 100.4% | 100.1% | 98.9% | 101.4% | 104.2% | 101.7% | 111.3% | 106.3% | 100.8% | 100.5% | 103.0% | 100.3% | 100.1% | 101.4% |
| 2014-12-01 | 101.4% | 96.4% | 106.5% | 97.1% | 99.7% | 101.9% | 106.7% | 98.2% | 100.6% | 107.8% | 100.3% | 100.9% | 100.1% | 100.6% | 99.0% | 100.5% | 102.0% | 100.8% | 100.8% | 103.6% | 98.1% | 101.0% | 104.6% | 99.5% | 102.4% | 97.2% | 98.7% | 101.9% | 103.2% | 95.7% | 100.1% | 97.5% | 97.3% | 105.0% | 100.6% | 129.4% | 99.6% | 104.2% | 100.9% | 100.2% | 99.0% | 101.6% | 104.4% | 101.9% | 111.6% | 106.6% | 100.6% | 100.6% | 103.5% | 100.3% | 99.9% | 101.8% |
| 2015-01-01 | 101.6% | 96.3% | 106.8% | 97.2% | 99.6% | 102.1% | 107.0% | 98.3% | 100.6% | 108.3% | 100.6% | 100.8% | 100.8% | 100.9% | 99.0% | 100.7% | 102.2% | 100.7% | 101.0% | 103.4% | 97.9% | 101.0% | 104.5% | 99.3% | 102.3% | 97.0% | 99.0% | 102.8% | 103.2% | 96.0% | 100.2% | 97.4% | 97.2% | 105.1% | 100.8% | 128.9% | 99.5% | 104.3% | 101.1% | 100.0% | 99.2% | 101.6% | 104.5% | 101.9% | 111.7% | 107.1% | 101.2% | 100.9% | 103.6% | 100.2% | 99.9% | 101.8% |
| 2015-02-01 | 101.8% | 96.5% | 106.6% | 97.4% | 99.9% | 102.3% | 107.3% | 98.2% | 100.7% | 108.4% | 100.8% | 101.1% | 100.9% | 101.0% | 99.0% | 100.6% | 102.2% | 100.9% | 100.9% | 103.2% | 97.7% | 101.2% | 104.3% | 99.3% | 102.5% | 97.1% | 99.3% | 103.0% | 103.5% | 96.2% | 100.0% | 97.5% | 97.2% | 105.1% | 101.0% | 128.3% | 99.6% | 104.3% | 101.4% | 100.1% | 98.5% | 101.9% | 104.6% | 102.0% | 111.7% | 107.5% | 101.0% | 101.0% | 103.8% | 100.1% | 100.0% | 101.7% |
| 2015-03-01 | 101.8% | 96.3% | 106.8% | 97.5% | 99.4% | 102.6% | 107.3% | 98.2% | 100.8% | 108.4% | 101.1% | 101.2% | 100.9% | 101.5% | 99.0% | 100.7% | 102.4% | 100.8% | 100.6% | 102.9% | 97.9% | 101.0% | 104.6% | 99.3% | 102.7% | 96.9% | 99.2% | 103.2% | 103.5% | 96.4% | 100.4% | 97.5% | 97.2% | 105.2% | 100.9% | 127.8% | 99.5% | 104.0% | 101.6% | 99.9% | 98.8% | 102.0% | 104.8% | 101.9% | 111.7% | 107.8% | 101.1% | 100.8% | 104.1% | 99.6% | 100.1% | 101.4% |
| 2015-04-01 | 102.0% | 96.6% | 106.4% | 97.7% | 99.7% | 102.8% | 107.4% | 98.3% | 100.7% | 108.2% | 101.3% | 101.2% | 101.1% | 101.4% | 99.4% | 100.8% | 102.2% | 100.6% | 100.8% | 102.8% | 98.0% | 101.4% | 104.8% | 99.4% | 103.0% | 97.3% | 99.6% | 103.2% | 103.7% | 96.6% | 100.4% | 97.5% | 96.9% | 105.3% | 101.1% | 126.6% | 99.7% | 103.8% | 102.1% | 100.1% | 99.3% | 102.0% | 104.8% | 102.4% | 111.8% | 107.9% | 101.1% | 101.4% | 104.2% | 99.7% | 100.2% | 101.3% |
| 2015-05-01 | 102.3% | 96.9% | 106.5% | 97.9% | 100.3% | 103.1% | 107.8% | 98.6% | 101.5% | 108.6% | 101.7% | 101.7% | 101.3% | 101.9% | 99.8% | 101.3% | 102.3% | 100.9% | 101.3% | 102.9% | 98.4% | 101.8% | 105.4% | 99.9% | 103.3% | 97.7% | 100.0% | 103.2% | 103.7% | 97.0% | 101.0% | 97.9% | 97.0% | 105.8% | 101.5% | 126.2% | 100.1% | 103.9% | 102.4% | 100.4% | 99.8% | 102.5% | 104.9% | 102.8% | 112.0% | 108.3% | 101.5% | 101.8% | 104.5% | 99.9% | 100.4% | 100.9% |
| 2015-06-01 | 102.4% | 96.9% | 106.3% | 98.0% | 100.4% | 103.4% | 108.0% | 98.7% | 101.6% | 108.8% | 102.0% | 102.2% | 101.5% | 102.1% | 99.9% | 101.5% | 102.4% | 101.1% | 101.5% | 102.9% | 98.5% | 101.8% | 105.5% | 99.8% | 103.2% | 97.6% | 100.0% | 103.1% | 103.9% | 97.1% | 101.0% | 98.0% | 97.1% | 106.0% | 101.7% | 125.4% | 100.1% | 103.9% | 102.8% | 100.5% | 99.6% | 102.8% | 105.0% | 103.0% | 112.3% | 108.7% | 101.3% | 102.0% | 105.0% | 99.5% | 100.4% | 100.4% |
| 2015-07-01 | 102.6% | 97.0% | 106.4% | 98.2% | 100.8% | 104.0% | 108.2% | 98.4% | 101.7% | 109.4% | 102.4% | 102.2% | 101.7% | 102.4% | 99.9% | 101.3% | 102.4% | 101.0% | 101.4% | 103.1% | 98.6% | 101.9% | 105.6% | 100.1% | 103.4% | 97.7% | 100.2% | 103.3% | 104.1% | 97.3% | 101.1% | 98.2% | 97.2% | 106.2% | 101.9% | 124.9% | 100.2% | 104.0% | 102.8% | 100.5% | 99.8% | 103.1% | 105.1% | 103.3% | 112.5% | 109.0% | 100.9% | 102.4% | 105.0% | 99.2% | 100.6% | 100.3% |
| 2015-08-01 | 102.7% | 97.2% | 106.0% | 98.7% | 101.0% | 104.3% | 108.3% | 98.4% | 101.7% | 109.5% | 102.7% | 102.5% | 102.4% | 102.5% | 99.9% | 101.6% | 102.2% | 101.0% | 101.7% | 103.1% | 98.6% | 102.1% | 105.7% | 100.1% | 103.4% | 97.9% | 100.2% | 103.4% | 104.2% | 97.7% | 101.0% | 98.3% | 97.2% | 106.3% | 102.0% | 124.5% | 100.3% | 103.9% | 103.1% | 100.6% | 99.6% | 103.4% | 105.0% | 103.5% | 112.6% | 109.3% | 101.0% | 102.6% | 105.3% | 99.2% | 100.8% | 100.4% |
| 2015-09-01 | 102.8% | 97.3% | 106.1% | 98.8% | 101.2% | 104.4% | 108.7% | 98.6% | 102.1% | 109.6% | 102.9% | 102.7% | 101.7% | 103.0% | 100.0% | 101.7% | 102.3% | 101.1% | 101.8% | 103.0% | 98.6% | 102.1% | 105.6% | 100.2% | 103.4% | 98.0% | 100.3% | 103.7% | 104.3% | 97.9% | 101.3% | 98.4% | 97.1% | 106.4% | 102.3% | 123.9% | 100.4% | 103.8% | 103.3% | 100.6% | 99.9% | 103.6% | 105.1% | 103.8% | 112.7% | 109.7% | 101.1% | 102.9% | 105.6% | 99.2% | 100.9% | 100.5% |
| 2015-10-01 | 103.0% | 97.5% | 105.9% | 99.2% | 101.3% | 104.8% | 108.9% | 98.7% | 102.2% | 110.1% | 103.4% | 103.1% | 102.4% | 103.2% | 100.1% | 101.9% | 102.5% | 101.1% | 102.1% | 103.0% | 98.7% | 102.4% | 106.0% | 100.6% | 103.8% | 98.3% | 100.5% | 104.1% | 104.5% | 98.3% | 101.5% | 98.6% | 97.3% | 106.6% | 102.6% | 123.4% | 100.5% | 103.8% | 103.8% | 100.6% | 100.1% | 104.0% | 105.3% | 104.2% | 112.8% | 110.1% | 101.4% | 103.1% | 105.7% | 99.2% | 101.0% | 100.1% |
| 2015-11-01 | 103.2% | 97.6% | 105.7% | 99.6% | 101.5% | 105.0% | 109.2% | 98.8% | 102.7% | 110.2% | 103.8% | 103.2% | 102.1% | 103.5% | 100.1% | 102.1% | 102.6% | 101.1% | 102.4% | 102.9% | 98.7% | 102.5% | 106.2% | 100.6% | 103.9% | 98.4% | 100.7% | 104.2% | 104.5% | 98.7% | 101.8% | 98.8% | 97.4% | 106.7% | 102.8% | 123.0% | 100.5% | 103.8% | 104.0% | 100.7% | 100.3% | 104.1% | 105.4% | 104.4% | 112.9% | 110.4% | 101.4% | 103.2% | 105.9% | 99.2% | 101.0% | 99.8% |
| 2015-12-01 | 103.4% | 97.7% | 105.6% | 99.6% | 101.7% | 105.2% | 109.4% | 98.7% | 102.5% | 110.6% | 104.1% | 103.6% | 102.7% | 103.8% | 100.3% | 102.2% | 102.7% | 101.1% | 102.4% | 102.8% | 98.8% | 102.7% | 106.4% | 100.9% | 104.0% | 98.5% | 100.8% | 104.4% | 104.7% | 99.1% | 101.9% | 98.8% | 97.1% | 106.8% | 103.2% | 122.4% | 100.7% | 103.6% | 104.4% | 100.8% | 100.4% | 104.5% | 105.6% | 104.6% | 113.0% | 110.6% | 101.2% | 103.4% | 106.2% | 99.3% | 101.2% | 99.4% |
| 2016-01-01 | 103.5% | 97.9% | 105.5% | 99.7% | 101.5% | 105.3% | 109.6% | 98.5% | 102.2% | 110.3% | 104.2% | 103.6% | 101.9% | 104.0% | 100.3% | 102.2% | 102.8% | 101.1% | 102.4% | 102.4% | 99.0% | 102.5% | 106.5% | 101.1% | 103.9% | 98.7% | 100.9% | 104.3% | 104.4% | 98.9% | 102.0% | 98.8% | 97.3% | 106.9% | 103.2% | 121.2% | 100.7% | 103.6% | 104.5% | 100.8% | 100.2% | 104.3% | 105.4% | 104.7% | 113.1% | 110.9% | 101.2% | 102.9% | 106.6% | 98.7% | 101.4% | 98.8% |
| 2016-02-01 | 103.6% | 97.9% | 105.2% | 100.1% | 101.8% | 105.6% | 109.8% | 98.7% | 102.2% | 110.7% | 104.5% | 103.8% | 102.4% | 104.5% | 100.3% | 102.4% | 102.9% | 101.2% | 102.4% | 102.2% | 99.2% | 102.4% | 106.7% | 101.1% | 104.1% | 98.9% | 100.9% | 104.4% | 104.4% | 99.1% | 102.4% | 98.9% | 97.6% | 107.0% | 103.3% | 120.7% | 100.8% | 103.6% | 105.0% | 100.8% | 100.4% | 104.6% | 105.4% | 104.8% | 113.2% | 111.3% | 101.2% | 103.1% | 107.0% | 98.4% | 101.5% | 98.4% |
| 2016-03-01 | 103.8% | 97.9% | 105.2% | 100.3% | 101.8% | 105.5% | 110.0% | 99.0% | 102.4% | 110.8% | 104.7% | 103.8% | 102.4% | 104.9% | 100.3% | 102.5% | 103.2% | 101.2% | 102.4% | 102.1% | 99.3% | 102.7% | 107.0% | 101.2% | 104.2% | 98.9% | 101.1% | 104.6% | 104.8% | 99.3% | 102.3% | 99.2% | 97.3% | 107.3% | 103.6% | 120.2% | 100.9% | 103.3% | 105.2% | 101.1% | 100.7% | 104.8% | 105.6% | 105.2% | 113.1% | 111.6% | 101.2% | 103.3% | 107.2% | 98.8% | 101.5% | 98.1% |
| 2016-04-01 | 103.9% | 98.2% | 105.4% | 100.6% | 101.9% | 106.1% | 110.2% | 98.8% | 102.5% | 110.9% | 105.1% | 104.3% | 102.6% | 105.0% | 100.4% | 102.4% | 103.2% | 101.4% | 102.5% | 102.1% | 99.5% | 102.9% | 107.1% | 101.8% | 104.7% | 98.8% | 101.4% | 104.7% | 104.9% | 99.7% | 102.7% | 99.3% | 97.4% | 107.5% | 104.0% | 120.4% | 101.1% | 103.2% | 105.4% | 101.2% | 100.4% | 105.0% | 105.8% | 105.3% | 113.4% | 112.0% | 101.1% | 103.5% | 107.6% | 98.6% | 101.9% | 97.7% |
| 2016-05-01 | 104.0% | 98.1% | 104.9% | 100.8% | 102.0% | 106.3% | 110.0% | 98.8% | 102.2% | 111.0% | 105.3% | 104.5% | 102.7% | 105.2% | 100.3% | 102.3% | 102.8% | 101.2% | 102.6% | 102.1% | 99.5% | 102.8% | 107.1% | 101.5% | 104.5% | 98.7% | 101.3% | 104.6% | 104.8% | 99.8% | 102.5% | 99.3% | 97.3% | 107.2% | 104.0% | 120.0% | 101.1% | 102.9% | 105.5% | 101.0% | 100.4% | 105.2% | 105.8% | 105.3% | 113.5% | 112.2% | 101.6% | 103.4% | 107.9% | 99.4% | 101.6% | 97.2% |
| 2016-06-01 | 104.2% | 98.1% | 104.1% | 100.6% | 102.1% | 106.2% | 110.4% | 98.6% | 102.4% | 111.0% | 105.4% | 104.7% | 102.6% | 105.4% | 100.3% | 102.3% | 102.6% | 101.0% | 102.4% | 101.9% | 99.5% | 102.8% | 106.9% | 101.6% | 104.1% | 98.4% | 101.4% | 104.6% | 104.8% | 100.0% | 102.5% | 99.4% | 97.1% | 107.4% | 104.1% | 119.8% | 100.9% | 102.6% | 105.7% | 101.0% | 100.4% | 105.2% | 105.9% | 105.5% | 113.3% | 112.5% | 101.3% | 103.5% | 108.0% | 97.6% | 101.5% | 96.9% |
| 2016-07-01 | 104.4% | 98.4% | 104.4% | 101.4% | 102.4% | 106.7% | 110.9% | 98.9% | 102.9% | 111.1% | 106.0% | 104.9% | 103.2% | 106.1% | 100.5% | 102.9% | 103.0% | 101.3% | 103.0% | 102.1% | 99.8% | 103.1% | 107.8% | 102.0% | 104.8% | 99.0% | 101.6% | 104.7% | 105.1% | 100.9% | 102.9% | 99.8% | 97.3% | 107.8% | 104.3% | 120.5% | 101.3% | 102.9% | 105.9% | 101.3% | 100.6% | 105.7% | 106.4% | 105.9% | 113.9% | 113.3% | 101.9% | 103.6% | 108.4% | 97.6% | 101.9% | 96.7% |
| 2016-08-01 | 104.5% | 98.4% | 104.2% | 101.4% | 102.4% | 106.8% | 111.1% | 98.9% | 102.8% | 111.1% | 106.2% | 105.1% | 103.8% | 106.4% | 100.5% | 102.8% | 103.0% | 101.1% | 103.0% | 101.5% | 99.8% | 103.3% | 107.9% | 101.9% | 105.1% | 98.8% | 101.7% | 104.9% | 105.0% | 101.1% | 102.9% | 99.9% | 97.2% | 107.8% | 104.4% | 120.4% | 101.2% | 102.9% | 106.2% | 101.3% | 100.6% | 105.9% | 106.1% | 106.1% | 113.9% | 113.3% | 101.5% | 103.8% | 108.6% | 97.6% | 102.1% | 96.4% |
| 2016-09-01 | 104.7% | 98.7% | 103.6% | 101.8% | 102.7% | 106.9% | 111.5% | 98.9% | 102.9% | 111.3% | 106.5% | 105.5% | 103.5% | 106.6% | 100.7% | 103.2% | 103.2% | 101.4% | 103.0% | 101.8% | 99.7% | 103.6% | 107.9% | 102.3% | 105.2% | 99.0% | 101.7% | 105.1% | 105.4% | 101.4% | 103.5% | 100.1% | 97.5% | 107.9% | 104.8% | 120.2% | 101.5% | 102.9% | 106.5% | 101.6% | 100.7% | 106.2% | 106.3% | 106.4% | 114.2% | 113.6% | 101.9% | 103.9% | 109.0% | 97.8% | 102.0% | 95.9% |
| 2016-10-01 | 104.8% | 98.5% | 103.8% | 101.9% | 102.6% | 107.2% | 111.4% | 98.9% | 102.8% | 111.5% | 106.6% | 105.5% | 103.3% | 106.6% | 100.9% | 103.0% | 103.1% | 101.3% | 103.0% | 101.6% | 99.8% | 103.5% | 107.8% | 102.2% | 105.1% | 98.9% | 101.8% | 105.0% | 105.2% | 101.4% | 103.2% | 100.0% | 97.0% | 107.9% | 104.6% | 119.8% | 101.5% | 102.7% | 106.7% | 101.5% | 100.8% | 105.8% | 106.2% | 106.4% | 114.2% | 113.6% | 101.7% | 104.0% | 109.0% | 97.7% | 102.0% | 95.9% |
| 2016-11-01 | 104.9% | 98.4% | 103.7% | 101.9% | 102.6% | 107.3% | 111.6% | 98.9% | 102.9% | 111.6% | 106.8% | 105.8% | 103.6% | 106.9% | 100.8% | 103.2% | 103.0% | 101.3% | 102.8% | 101.7% | 100.1% | 103.7% | 107.9% | 102.5% | 105.1% | 99.0% | 101.8% | 105.3% | 105.0% | 101.6% | 103.3% | 100.1% | 97.0% | 108.0% | 105.0% | 119.6% | 101.6% | 102.7% | 107.1% | 101.5% | 100.7% | 106.3% | 106.2% | 106.4% | 114.3% | 113.8% | 101.6% | 104.1% | 109.3% | 99.1% | 102.3% | 96.0% |
| 2016-12-01 | 105.1% | 98.6% | 103.8% | 102.1% | 102.7% | 107.5% | 111.7% | 99.0% | 103.0% | 111.8% | 107.0% | 105.9% | 103.5% | 107.1% | 100.9% | 103.1% | 103.0% | 101.3% | 103.0% | 101.7% | 99.9% | 103.8% | 108.1% | 102.4% | 105.1% | 99.0% | 101.9% | 105.3% | 104.8% | 101.8% | 103.3% | 100.3% | 97.3% | 108.2% | 105.1% | 119.1% | 101.5% | 102.7% | 107.0% | 101.6% | 100.8% | 106.5% | 106.2% | 106.7% | 114.5% | 113.9% | 101.7% | 104.1% | 109.4% | 98.0% | 101.9% | 95.6% |
| 2017-01-01 | 105.2% | 98.9% | 103.4% | 102.2% | 102.8% | 107.4% | 111.8% | 99.1% | 103.5% | 111.8% | 107.3% | 105.8% | 103.8% | 107.5% | 100.7% | 103.3% | 102.8% | 101.0% | 103.1% | 101.7% | 100.2% | 103.9% | 108.2% | 102.7% | 105.7% | 99.0% | 102.0% | 105.3% | 105.0% | 102.3% | 103.4% | 100.4% | 97.2% | 108.5% | 105.0% | 119.1% | 101.7% | 102.7% | 106.5% | 101.8% | 100.9% | 106.6% | 106.1% | 106.5% | 114.8% | 114.4% | 102.0% | 104.2% | 109.5% | 98.1% | 102.2% | 95.7% |
| 2017-02-01 | 105.4% | 99.0% | 103.6% | 102.6% | 103.0% | 107.7% | 112.2% | 99.0% | 103.4% | 111.8% | 107.4% | 105.9% | 103.9% | 107.6% | 100.9% | 103.3% | 103.0% | 101.3% | 103.3% | 102.1% | 100.0% | 104.0% | 108.2% | 102.6% | 105.8% | 99.2% | 102.4% | 105.4% | 105.3% | 102.7% | 103.4% | 100.5% | 97.3% | 108.6% | 105.2% | 119.3% | 101.8% | 102.8% | 107.4% | 101.8% | 101.0% | 106.9% | 106.1% | 106.9% | 114.9% | 114.6% | 101.4% | 104.4% | 109.8% | 98.3% | 102.2% | 95.8% |
| 2017-03-01 | 105.5% | 99.2% | 103.4% | 102.9% | 103.2% | 108.0% | 112.6% | 99.1% | 103.4% | 112.2% | 107.6% | 106.2% | 104.1% | 108.2% | 101.0% | 103.5% | 103.1% | 101.5% | 103.3% | 101.9% | 100.4% | 104.1% | 108.4% | 102.8% | 106.1% | 99.3% | 102.3% | 105.7% | 105.3% | 103.4% | 103.6% | 100.5% | 97.5% | 108.6% | 105.4% | 119.4% | 101.9% | 103.1% | 107.7% | 101.8% | 100.9% | 107.2% | 106.2% | 106.9% | 115.3% | 115.1% | 101.8% | 104.5% | 110.1% | 98.3% | 102.4% | 95.9% |
| 2017-04-01 | 105.6% | 99.0% | 103.2% | 103.2% | 103.4% | 108.2% | 112.7% | 98.9% | 103.3% | 112.0% | 107.7% | 106.3% | 104.2% | 108.1% | 101.0% | 103.6% | 103.2% | 100.8% | 103.3% | 101.8% | 100.2% | 104.1% | 108.5% | 102.9% | 105.9% | 99.2% | 102.2% | 105.8% | 105.3% | 103.0% | 103.9% | 100.5% | 97.6% | 108.5% | 105.5% | 120.1% | 101.9% | 103.3% | 108.0% | 102.0% | 101.2% | 107.0% | 106.7% | 107.1% | 115.4% | 115.2% | 102.0% | 104.6% | 110.4% | 97.9% | 102.4% | 95.9% |
| 2017-05-01 | 105.8% | 99.2% | 103.4% | 103.3% | 103.3% | 108.5% | 112.8% | 99.1% | 103.0% | 112.1% | 108.0% | 106.4% | 104.2% | 108.5% | 101.1% | 103.7% | 102.9% | 100.8% | 103.2% | 102.0% | 100.2% | 104.1% | 108.6% | 103.0% | 105.8% | 99.1% | 102.2% | 105.8% | 105.1% | 103.3% | 103.8% | 100.8% | 97.5% | 108.8% | 105.7% | 119.8% | 101.9% | 103.3% | 108.2% | 102.1% | 101.3% | 107.3% | 106.3% | 107.1% | 115.6% | 115.4% | 102.0% | 104.6% | 110.6% | 98.0% | 102.6% | 96.4% |
| 2017-06-01 | 105.9% | 99.3% | 103.4% | 103.7% | 103.5% | 108.8% | 113.0% | 99.2% | 103.5% | 112.0% | 108.2% | 106.8% | 104.3% | 108.9% | 101.3% | 104.0% | 103.1% | 100.9% | 103.4% | 102.1% | 100.5% | 104.2% | 108.8% | 103.1% | 106.1% | 99.3% | 102.6% | 106.2% | 105.3% | 103.5% | 104.0% | 101.0% | 98.0% | 109.0% | 105.9% | 119.6% | 102.0% | 103.8% | 108.6% | 102.2% | 101.5% | 107.5% | 106.4% | 107.4% | 115.9% | 115.9% | 102.6% | 104.8% | 110.9% | 97.8% | 102.7% | 96.3% |
| 2017-07-01 | 106.1% | 99.3% | 103.2% | 103.7% | 103.6% | 108.8% | 113.2% | 99.1% | 103.3% | 112.0% | 108.3% | 106.8% | 104.1% | 108.9% | 101.2% | 103.8% | 103.0% | 101.1% | 103.2% | 101.9% | 100.5% | 104.1% | 109.0% | 102.8% | 106.1% | 99.3% | 102.4% | 105.9% | 105.1% | 103.6% | 104.1% | 101.0% | 97.7% | 109.1% | 106.1% | 119.6% | 101.9% | 103.9% | 108.7% | 102.3% | 101.4% | 107.8% | 106.2% | 107.5% | 115.7% | 116.1% | 102.0% | 104.8% | 111.0% | 97.9% | 102.6% | 96.4% |
| 2017-08-01 | 106.2% | 99.4% | 103.4% | 103.9% | 103.7% | 108.9% | 113.5% | 99.1% | 103.4% | 112.1% | 108.4% | 107.1% | 103.6% | 109.2% | 101.4% | 103.8% | 103.1% | 100.9% | 103.1% | 101.8% | 100.5% | 104.2% | 109.1% | 103.0% | 106.1% | 99.3% | 102.5% | 106.0% | 105.1% | 103.7% | 104.1% | 101.1% | 97.7% | 109.2% | 106.2% | 119.4% | 102.1% | 104.0% | 108.8% | 102.3% | 101.7% | 107.6% | 106.4% | 107.6% | 115.8% | 116.3% | 102.2% | 104.9% | 111.0% | 97.8% | 102.6% | 96.5% |
| 2017-09-01 | 106.2% | 99.5% | 103.3% | 104.3% | 103.9% | 109.2% | 113.8% | 99.1% | 103.8% | 112.0% | 106.4% | 106.9% | 104.5% | 109.6% | 101.5% | 104.2% | 103.2% | 101.4% | 103.5% | 102.0% | 100.8% | 104.3% | 109.1% | 103.2% | 106.4% | 99.3% | 102.6% | 106.1% | 105.2% | 104.1% | 104.0% | 101.3% | 98.0% | 109.3% | 106.4% | 119.1% | 102.1% | 104.1% | 109.0% | 102.5% | 101.5% | 107.6% | 106.5% | 107.8% | 116.0% | 116.7% | 102.1% | 105.0% | 111.2% | 98.1% | 102.8% | 96.6% |
| 2017-10-01 | 106.3% | 99.7% | 102.7% | 104.4% | 104.0% | 109.4% | 114.0% | 99.0% | 103.4% | 112.5% | 108.7% | 107.4% | 104.4% | 109.7% | 101.5% | 104.1% | 103.2% | 101.4% | 103.7% | 101.8% | 100.6% | 104.5% | 109.1% | 103.1% | 106.3% | 99.3% | 102.3% | 106.0% | 105.4% | 104.3% | 104.2% | 101.4% | 97.7% | 109.4% | 106.5% | 119.3% | 102.2% | 104.0% | 108.9% | 102.5% | 101.4% | 108.2% | 106.7% | 107.9% | 116.4% | 117.0% | 102.1% | 105.1% | 111.5% | 98.3% | 102.8% | 96.1% |
| 2017-11-01 | 106.5% | 99.6% | 102.7% | 104.5% | 104.1% | 109.5% | 114.0% | 99.0% | 103.7% | 112.5% | 109.0% | 107.5% | 104.2% | 109.9% | 101.6% | 104.2% | 103.3% | 101.6% | 103.6% | 101.9% | 100.9% | 104.5% | 109.3% | 103.3% | 106.4% | 99.4% | 102.5% | 106.1% | 105.4% | 104.6% | 104.2% | 101.4% | 97.9% | 109.6% | 106.5% | 119.3% | 102.2% | 104.0% | 109.1% | 102.6% | 101.6% | 108.3% | 106.5% | 108.0% | 116.6% | 117.3% | 102.3% | 105.0% | 111.7% | 98.2% | 102.8% | 96.1% |
| 2017-12-01 | 106.6% | 99.6% | 102.6% | 104.8% | 104.2% | 109.8% | 114.5% | 98.9% | 103.9% | 112.7% | 109.2% | 107.6% | 104.5% | 110.3% | 101.7% | 104.3% | 103.5% | 101.7% | 103.6% | 102.0% | 101.2% | 104.5% | 109.4% | 103.3% | 106.5% | 99.3% | 102.6% | 106.3% | 105.6% | 105.1% | 104.3% | 101.5% | 98.1% | 109.8% | 106.6% | 119.5% | 102.3% | 104.2% | 109.3% | 102.8% | 101.7% | 108.5% | 106.7% | 108.2% | 116.8% | 117.7% | 102.5% | 105.4% | 112.0% | 98.2% | 102.9% | 96.2% |
| 2018-01-01 | 106.7% | 99.8% | 102.6% | 105.0% | 104.3% | 110.1% | 114.8% | 99.0% | 104.0% | 113.0% | 109.4% | 107.5% | 104.4% | 110.8% | 101.6% | 104.3% | 103.5% | 101.5% | 103.3% | 102.0% | 101.0% | 104.6% | 109.4% | 103.6% | 106.8% | 99.1% | 102.4% | 106.6% | 105.5% | 105.3% | 104.2% | 101.3% | 98.4% | 109.6% | 106.7% | 119.7% | 102.2% | 104.7% | 109.6% | 102.8% | 101.2% | 109.6% | 107.0% | 108.1% | 116.9% | 118.1% | 101.6% | 105.5% | 112.6% | 98.6% | 103.2% | 96.3% |
| 2018-02-01 | 107.0% | 100.0% | 102.7% | 105.6% | 104.5% | 110.4% | 115.0% | 99.2% | 104.4% | 113.2% | 109.7% | 107.8% | 104.6% | 111.2% | 101.9% | 104.5% | 103.7% | 101.9% | 103.7% | 102.1% | 101.2% | 104.9% | 109.8% | 103.8% | 106.9% | 99.1% | 102.6% | 106.6% | 105.6% | 106.1% | 104.5% | 101.6% | 98.6% | 110.0% | 107.0% | 119.8% | 102.5% | 104.6% | 109.8% | 103.0% | 101.7% | 109.9% | 107.1% | 108.5% | 117.3% | 118.7% | 102.4% | 105.7% | 112.8% | 98.7% | 103.4% | 96.3% |
| 2018-03-01 | 107.2% | 100.2% | 102.8% | 105.9% | 104.6% | 110.5% | 115.4% | 99.1% | 104.4% | 113.3% | 110.0% | 108.2% | 104.7% | 111.4% | 102.1% | 104.7% | 103.7% | 101.8% | 103.8% | 102.7% | 101.2% | 105.0% | 109.8% | 104.1% | 106.8% | 99.4% | 102.7% | 106.8% | 105.7% | 106.5% | 104.5% | 101.5% | 98.6% | 110.1% | 107.4% | 120.2% | 102.6% | 105.0% | 110.0% | 103.1% | 101.7% | 110.1% | 107.2% | 108.7% | 117.7% | 118.9% | 102.3% | 105.9% | 113.1% | 98.8% | 103.5% | 96.4% |
| 2018-04-01 | 107.3% | 100.3% | 102.5% | 105.9% | 104.6% | 110.5% | 115.6% | 98.9% | 104.6% | 113.5% | 110.1% | 108.2% | 104.6% | 111.8% | 101.7% | 104.6% | 103.5% | 101.8% | 103.9% | 102.7% | 101.4% | 105.0% | 109.8% | 103.9% | 106.4% | 99.5% | 102.6% | 106.6% | 105.6% | 106.5% | 104.4% | 101.6% | 98.8% | 110.1% | 107.6% | 119.6% | 102.4% | 104.7% | 109.9% | 103.2% | 101.8% | 110.4% | 106.6% | 108.7% | 117.8% | 119.0% | 102.3% | 106.0% | 113.0% | 99.0% | 103.2% | 96.6% |
| 2018-05-01 | 107.5% | 100.4% | 102.7% | 106.2% | 104.8% | 110.6% | 115.8% | 99.2% | 105.0% | 113.4% | 110.3% | 108.5% | 104.5% | 112.0% | 101.8% | 104.7% | 103.9% | 101.8% | 103.9% | 102.7% | 101.4% | 105.1% | 109.9% | 104.1% | 106.9% | 99.5% | 102.6% | 107.0% | 105.9% | 106.6% | 104.6% | 101.7% | 98.8% | 110.3% | 107.9% | 120.5% | 102.5% | 105.0% | 110.2% | 103.3% | 102.2% | 110.6% | 107.3% | 109.0% | 118.2% | 119.2% | 102.2% | 106.1% | 113.2% | 100.3% | 103.5% | 96.9% |
| 2018-06-01 | 107.7% | 100.7% | 102.7% | 106.4% | 104.7% | 110.9% | 116.1% | 99.4% | 104.8% | 113.4% | 110.6% | 108.7% | 104.7% | 112.5% | 102.1% | 105.0% | 104.0% | 101.9% | 104.1% | 102.8% | 101.8% | 105.2% | 109.9% | 104.3% | 107.0% | 99.4% | 103.1% | 107.5% | 105.9% | 106.6% | 104.8% | 101.8% | 99.4% | 110.6% | 108.1% | 120.8% | 102.7% | 105.3% | 110.4% | 103.4% | 102.0% | 110.8% | 107.3% | 109.3% | 118.5% | 119.7% | 102.2% | 106.2% | 113.3% | 99.5% | 103.7% | 96.9% |
| 2018-07-01 | 107.7% | 100.8% | 102.6% | 106.7% | 105.1% | 110.8% | 116.2% | 99.3% | 104.6% | 113.3% | 110.7% | 108.9% | 104.3% | 112.8% | 102.1% | 105.0% | 103.9% | 102.1% | 103.8% | 102.7% | 101.4% | 105.3% | 109.9% | 104.1% | 107.1% | 99.3% | 103.0% | 107.2% | 106.0% | 106.8% | 104.8% | 101.9% | 99.2% | 110.6% | 108.2% | 120.8% | 102.7% | 105.4% | 110.3% | 103.5% | 102.1% | 110.7% | 107.3% | 109.2% | 118.7% | 119.8% | 102.8% | 106.3% | 113.4% | 99.8% | 103.5% | 97.1% |
| 2018-08-01 | 107.9% | 100.9% | 102.6% | 107.1% | 105.3% | 111.1% | 116.4% | 99.4% | 104.5% | 113.3% | 111.1% | 109.2% | 104.5% | 113.1% | 102.2% | 105.1% | 103.8% | 102.3% | 103.9% | 102.9% | 101.5% | 105.4% | 109.9% | 104.2% | 107.1% | 99.6% | 103.1% | 107.4% | 105.9% | 107.3% | 104.7% | 102.0% | 99.4% | 110.7% | 108.3% | 120.7% | 102.8% | 105.6% | 110.6% | 103.5% | 102.1% | 110.8% | 107.5% | 109.6% | 119.1% | 120.2% | 102.6% | 106.3% | 113.7% | 99.9% | 103.8% | 97.2% |
| 2018-09-01 | 107.9% | 101.1% | 102.5% | 107.4% | 105.5% | 111.3% | 116.4% | 99.3% | 104.7% | 113.3% | 111.4% | 109.4% | 104.6% | 113.0% | 102.2% | 105.1% | 103.9% | 102.4% | 104.1% | 102.9% | 101.7% | 105.3% | 110.1% | 104.1% | 107.3% | 99.6% | 103.1% | 107.4% | 106.0% | 107.6% | 104.6% | 102.0% | 99.5% | 110.7% | 107.8% | 120.7% | 102.9% | 105.6% | 110.8% | 103.7% | 102.2% | 110.4% | 107.6% | 109.8% | 119.2% | 120.6% | 102.4% | 106.3% | 113.9% | 99.9% | 103.6% | 97.0% |
| 2018-10-01 | 108.0% | 101.2% | 102.9% | 107.5% | 105.6% | 111.5% | 116.6% | 99.3% | 105.0% | 113.6% | 111.5% | 109.3% | 104.8% | 113.5% | 102.1% | 105.1% | 103.9% | 102.2% | 104.1% | 103.1% | 102.1% | 105.4% | 110.2% | 104.4% | 107.1% | 99.6% | 103.0% | 107.4% | 105.8% | 107.9% | 104.9% | 102.2% | 99.3% | 110.9% | 108.6% | 120.9% | 102.9% | 105.7% | 111.0% | 103.8% | 102.2% | 111.1% | 107.6% | 109.8% | 119.4% | 120.8% | 102.5% | 106.4% | 114.2% | 100.1% | 103.6% | 97.4% |
| 2018-11-01 | 108.1% | 101.3% | 102.8% | 107.8% | 105.7% | 111.6% | 116.9% | 99.3% | 104.9% | 113.5% | 111.7% | 109.4% | 105.1% | 113.7% | 102.3% | 105.1% | 104.1% | 102.4% | 104.2% | 103.0% | 102.1% | 105.5% | 110.3% | 104.5% | 107.4% | 99.7% | 103.1% | 107.9% | 106.0% | 108.3% | 105.1% | 102.4% | 99.7% | 111.0% | 108.6% | 121.0% | 102.9% | 105.8% | 111.2% | 103.8% | 102.2% | 111.2% | 107.6% | 110.0% | 119.6% | 121.1% | 102.6% | 106.6% | 114.4% | 99.8% | 103.8% | 97.7% |
| 2018-12-01 | 108.3% | 101.4% | 102.7% | 108.0% | 105.7% | 111.9% | 117.1% | 99.4% | 105.2% | 113.6% | 111.7% | 109.5% | 105.0% | 114.0% | 102.2% | 105.1% | 104.0% | 102.4% | 104.0% | 102.9% | 102.2% | 105.5% | 110.6% | 104.4% | 107.4% | 99.5% | 103.1% | 108.1% | 105.8% | 108.5% | 105.0% | 102.3% | 99.8% | 111.1% | 108.4% | 121.3% | 102.9% | 105.9% | 111.3% | 103.9% | 102.3% | 111.2% | 107.8% | 110.0% | 119.8% | 121.3% | 102.6% | 106.6% | 114.4% | 99.6% | 103.8% | 97.8% |
| 2019-01-01 | 108.5% | 101.7% | 103.1% | 108.4% | 106.1% | 111.9% | 117.4% | 99.0% | 105.5% | 113.6% | 111.9% | 110.0% | 104.5% | 114.3% | 102.2% | 105.8% | 104.1% | 102.2% | 104.4% | 102.9% | 102.3% | 105.7% | 110.7% | 104.5% | 107.5% | 99.9% | 103.2% | 108.0% | 106.2% | 109.0% | 105.3% | 102.4% | 99.9% | 111.3% | 109.2% | 121.5% | 103.1% | 106.0% | 111.7% | 104.1% | 102.6% | 111.4% | 108.0% | 110.5% | 120.0% | 121.7% | 102.5% | 106.8% | 114.9% | 99.5% | 103.9% | 98.0% |
| 2019-02-01 | 108.5% | 101.7% | 103.1% | 108.7% | 106.2% | 112.0% | 117.8% | 99.1% | 105.6% | 114.0% | 112.3% | 110.1% | 104.8% | 114.5% | 102.2% | 105.9% | 103.9% | 102.4% | 104.4% | 103.1% | 102.3% | 105.8% | 111.0% | 104.4% | 107.3% | 99.9% | 103.3% | 107.8% | 105.9% | 109.5% | 105.5% | 102.5% | 100.2% | 111.4% | 109.2% | 121.4% | 103.1% | 106.2% | 111.3% | 104.0% | 102.6% | 111.5% | 107.8% | 110.7% | 120.3% | 122.0% | 102.8% | 107.0% | 114.2% | 99.2% | 103.6% | 98.5% |
| 2019-03-01 | 108.6% | 101.8% | 103.3% | 108.9% | 106.1% | 112.2% | 117.7% | 99.0% | 105.9% | 114.1% | 112.4% | 110.3% | 104.7% | 114.6% | 102.2% | 105.8% | 103.9% | 102.2% | 104.5% | 102.9% | 102.4% | 105.9% | 111.0% | 104.6% | 107.4% | 99.8% | 103.3% | 107.6% | 105.6% | 109.8% | 105.6% | 102.6% | 100.3% | 111.6% | 109.5% | 121.5% | 103.2% | 106.2% | 111.6% | 104.2% | 102.5% | 111.8% | 107.6% | 110.8% | 120.4% | 122.2% | 103.4% | 107.1% | 115.0% | 99.2% | 103.8% | 98.4% |
| 2019-04-01 | 108.8% | 102.1% | 103.3% | 109.2% | 106.1% | 112.1% | 118.1% | 99.1% | 105.8% | 114.0% | 112.5% | 110.3% | 104.5% | 115.1% | 102.3% | 105.4% | 104.1% | 102.9% | 104.5% | 103.1% | 102.4% | 105.8% | 111.5% | 104.5% | 107.4% | 99.8% | 103.5% | 108.0% | 105.9% | 109.7% | 105.5% | 102.6% | 100.2% | 111.6% | 109.7% | 121.7% | 103.3% | 106.3% | 111.9% | 104.3% | 102.6% | 112.1% | 107.6% | 110.9% | 120.7% | 122.6% | 102.9% | 107.2% | 115.3% | 99.3% | 103.8% | 98.3% |
| 2019-05-01 | 108.9% | 102.2% | 103.3% | 109.3% | 106.1% | 112.3% | 118.6% | 99.1% | 105.7% | 114.0% | 112.6% | 110.5% | 104.6% | 115.4% | 102.4% | 105.1% | 104.1% | 102.7% | 104.5% | 103.0% | 102.6% | 105.9% | 111.6% | 104.6% | 107.8% | 99.9% | 103.5% | 108.4% | 105.9% | 109.8% | 105.6% | 102.6% | 100.4% | 111.6% | 109.9% | 122.0% | 103.2% | 106.2% | 112.1% | 104.3% | 102.6% | 112.3% | 107.7% | 111.1% | 121.0% | 122.9% | 102.6% | 107.3% | 115.6% | 99.1% | 103.8% | 98.6% |
| 2019-06-01 | 109.0% | 102.3% | 103.9% | 109.4% | 105.9% | 112.5% | 118.8% | 99.1% | 105.8% | 114.0% | 112.8% | 110.7% | 104.4% | 115.6% | 102.6% | 105.5% | 103.9% | 102.6% | 104.6% | 102.8% | 102.8% | 106.0% | 111.7% | 104.5% | 107.8% | 99.9% | 103.5% | 108.4% | 106.0% | 109.4% | 105.7% | 102.7% | 100.5% | 111.7% | 110.1% | 122.0% | 103.2% | 106.1% | 112.2% | 104.2% | 102.5% | 112.4% | 107.8% | 111.3% | 121.2% | 122.9% | 102.8% | 107.4% | 115.8% | 99.0% | 104.1% | 98.6% |
| 2019-07-01 | 109.1% | 102.4% | 103.8% | 109.6% | 106.1% | 112.5% | 119.0% | 99.1% | 105.9% | 113.9% | 113.0% | 110.7% | 104.6% | 115.9% | 102.5% | 105.3% | 103.9% | 102.3% | 104.7% | 102.4% | 102.4% | 105.7% | 111.7% | 104.4% | 107.8% | 99.9% | 103.7% | 108.6% | 106.1% | 109.5% | 105.7% | 102.9% | 101.0% | 111.7% | 110.2% | 121.9% | 103.3% | 106.4% | 112.3% | 104.4% | 102.7% | 112.5% | 108.0% | 111.2% | 121.5% | 123.1% | 102.2% | 107.4% | 115.9% | 98.9% | 103.8% | 98.7% |
| 2019-08-01 | 109.2% | 102.5% | 103.4% | 110.5% | 106.1% | 112.8% | 119.3% | 98.9% | 106.0% | 113.9% | 113.4% | 111.0% | 104.3% | 116.3% | 102.5% | 105.5% | 103.9% | 102.8% | 104.9% | 102.9% | 102.8% | 105.8% | 111.7% | 104.7% | 107.9% | 100.0% | 103.8% | 109.0% | 106.1% | 109.8% | 105.8% | 102.9% | 101.2% | 111.7% | 110.3% | 122.1% | 103.3% | 106.3% | 112.6% | 104.6% | 102.8% | 112.7% | 108.1% | 111.5% | 121.7% | 123.5% | 102.1% | 107.5% | 116.1% | 99.0% | 103.7% | 98.9% |
| 2019-09-01 | 109.3% | 102.5% | 104.0% | 110.4% | 106.3% | 112.9% | 119.3% | 99.0% | 105.9% | 114.0% | 113.3% | 111.1% | 105.1% | 116.3% | 102.4% | 105.4% | 104.1% | 102.7% | 105.0% | 102.9% | 103.0% | 105.7% | 111.7% | 104.5% | 107.9% | 99.8% | 103.8% | 108.8% | 106.2% | 110.0% | 105.8% | 102.9% | 101.2% | 111.8% | 110.5% | 121.6% | 103.3% | 106.4% | 112.6% | 104.6% | 102.7% | 112.8% | 108.1% | 111.6% | 121.9% | 123.7% | 102.0% | 107.5% | 116.1% | 98.6% | 103.6% | 98.6% |
| 2019-10-01 | 109.4% | 102.4% | 103.4% | 110.6% | 106.6% | 113.0% | 119.4% | 99.1% | 105.8% | 114.2% | 113.7% | 111.2% | 105.1% | 116.7% | 102.4% | 105.5% | 104.2% | 102.7% | 104.8% | 102.7% | 102.8% | 106.1% | 111.7% | 104.0% | 108.0% | 99.7% | 103.9% | 109.0% | 106.3% | 110.2% | 105.8% | 102.9% | 101.3% | 111.6% | 110.5% | 121.9% | 103.3% | 106.3% | 112.7% | 104.6% | 102.7% | 112.9% | 108.3% | 111.2% | 122.0% | 123.9% | 102.0% | 107.9% | 116.3% | 98.5% | 103.8% | 98.8% |
| 2019-11-01 | 109.5% | 102.5% | 103.2% | 110.9% | 106.9% | 113.4% | 119.5% | 99.1% | 106.1% | 114.3% | 114.0% | 111.3% | 105.1% | 117.1% | 102.4% | 105.8% | 104.2% | 102.9% | 105.0% | 102.9% | 102.9% | 106.2% | 112.0% | 104.6% | 108.0% | 99.7% | 104.1% | 109.1% | 106.4% | 111.2% | 105.9% | 103.1% | 101.4% | 111.9% | 110.6% | 121.6% | 103.4% | 106.4% | 112.9% | 104.7% | 102.9% | 112.8% | 108.4% | 111.7% | 122.3% | 124.2% | 102.3% | 108.0% | 116.5% | 98.2% | 103.8% | 98.4% |
| 2019-12-01 | 109.7% | 102.6% | 103.2% | 111.3% | 107.0% | 113.5% | 119.6% | 98.8% | 106.1% | 114.5% | 114.1% | 111.5% | 104.9% | 117.5% | 102.5% | 105.8% | 104.3% | 103.0% | 105.0% | 102.7% | 102.9% | 106.2% | 112.1% | 104.9% | 108.0% | 99.5% | 104.1% | 109.1% | 106.5% | 111.6% | 106.0% | 103.1% | 101.5% | 111.9% | 110.6% | 121.7% | 103.5% | 106.3% | 113.1% | 104.7% | 102.9% | 112.8% | 108.3% | 111.7% | 122.3% | 124.2% | 102.1% | 108.0% | 116.9% | 98.3% | 104.0% | 98.5% |
| 2020-01-01 | 109.9% | 102.7% | 103.2% | 111.6% | 107.3% | 114.1% | 120.0% | 99.3% | 106.3% | 115.1% | 114.2% | 111.8% | 105.7% | 117.8% | 102.8% | 105.7% | 104.4% | 103.2% | 105.3% | 102.8% | 103.2% | 106.1% | 112.3% | 104.7% | 108.2% | 100.0% | 103.9% | 109.5% | 106.8% | 111.7% | 106.3% | 103.3% | 101.8% | 112.1% | 110.9% | 121.7% | 103.6% | 106.2% | 113.1% | 104.8% | 103.1% | 112.9% | 108.4% | 112.3% | 122.6% | 124.3% | 102.3% | 108.3% | 117.1% | 99.0% | 104.1% | 98.6% |
| 2020-02-01 | 110.2% | 102.7% | 103.3% | 111.8% | 107.4% | 114.3% | 120.0% | 99.2% | 106.4% | 115.1% | 114.4% | 111.9% | 105.5% | 117.9% | 102.7% | 105.8% | 104.3% | 103.0% | 105.5% | 102.8% | 103.1% | 106.3% | 112.7% | 104.8% | 108.2% | 100.2% | 104.0% | 109.6% | 106.7% | 112.1% | 106.5% | 103.5% | 101.6% | 112.3% | 111.0% | 121.7% | 103.6% | 106.1% | 113.3% | 104.9% | 103.4% | 112.8% | 108.7% | 112.3% | 122.7% | 124.4% | 102.3% | 108.3% | 117.4% | 98.8% | 104.1% | 98.3% |
| 2020-03-01 | 109.1% | 102.3% | 103.0% | 111.2% | 107.0% | 113.1% | 119.4% | 98.4% | 105.4% | 114.6% | 113.4% | 111.2% | 104.2% | 117.8% | 101.7% | 104.9% | 103.8% | 102.5% | 104.7% | 101.6% | 102.4% | 105.1% | 111.6% | 103.9% | 107.4% | 99.5% | 103.4% | 109.0% | 106.1% | 111.3% | 105.4% | 102.7% | 101.1% | 110.9% | 110.3% | 121.1% | 102.7% | 105.4% | 112.3% | 104.0% | 102.3% | 112.1% | 108.0% | 111.7% | 122.1% | 124.0% | 101.3% | 107.7% | 116.6% | 98.0% | 103.5% | 97.9% |
| 2020-04-01 | 94.3% | 90.7% | 88.8% | 99.1% | 96.8% | 96.5% | 104.0% | 82.3% | 90.9% | 103.1% | 98.2% | 97.1% | 81.0% | 105.8% | 88.9% | 89.3% | 92.7% | 91.7% | 89.5% | 88.2% | 87.7% | 90.9% | 92.0% | 80.0% | 93.1% | 87.4% | 91.3% | 95.3% | 96.6% | 86.3% | 88.3% | 85.6% | 89.4% | 89.6% | 97.6% | 106.8% | 87.3% | 95.6% | 97.1% | 85.4% | 81.4% | 97.1% | 97.7% | 98.8% | 109.0% | 113.1% | 81.0% | 95.6% | 103.3% | 84.6% | 90.1% | 89.7% |
| 2020-05-01 | 96.2% | 93.2% | 88.9% | 102.1% | 99.2% | 97.6% | 107.1% | 84.1% | 92.2% | 102.6% | 101.2% | 100.3% | 80.7% | 109.5% | 89.1% | 93.4% | 93.3% | 93.7% | 91.1% | 89.4% | 89.9% | 92.0% | 93.4% | 82.9% | 93.9% | 90.2% | 93.2% | 100.4% | 97.5% | 85.5% | 91.1% | 86.0% | 89.3% | 91.3% | 99.3% | 109.3% | 90.5% | 97.5% | 98.1% | 88.8% | 84.4% | 100.5% | 99.1% | 100.9% | 111.3% | 116.6% | 85.3% | 96.0% | 103.0% | 86.1% | 92.0% | 89.2% |
| 2020-06-01 | 99.5% | 95.6% | 89.3% | 104.7% | 101.3% | 100.8% | 109.3% | 87.5% | 96.8% | 102.8% | 104.9% | 102.9% | 83.5% | 112.7% | 91.1% | 97.3% | 95.9% | 95.4% | 95.9% | 91.5% | 91.6% | 94.1% | 95.9% | 90.8% | 96.4% | 93.4% | 95.7% | 103.1% | 99.4% | 92.3% | 94.3% | 87.4% | 91.3% | 94.1% | 102.7% | 110.0% | 94.7% | 99.8% | 101.4% | 92.4% | 89.0% | 104.0% | 101.4% | 104.7% | 113.4% | 118.7% | 88.7% | 98.0% | 105.7% | 91.0% | 95.0% | 89.5% |
| 2020-07-01 | 100.5% | 96.6% | 89.4% | 104.2% | 101.9% | 101.2% | 110.4% | 89.3% | 98.2% | 103.5% | 105.6% | 103.4% | 84.2% | 114.1% | 93.0% | 99.3% | 97.4% | 96.7% | 97.4% | 92.5% | 92.7% | 96.5% | 98.3% | 93.5% | 98.0% | 94.4% | 97.9% | 103.9% | 100.7% | 95.1% | 96.0% | 90.7% | 91.8% | 95.5% | 104.0% | 111.3% | 95.6% | 100.2% | 103.1% | 94.5% | 91.1% | 104.3% | 102.6% | 104.9% | 113.6% | 120.1% | 90.2% | 99.4% | 107.0% | 90.3% | 96.4% | 90.1% |
| 2020-08-01 | 101.7% | 97.7% | 91.0% | 105.2% | 103.1% | 101.8% | 111.6% | 90.8% | 99.6% | 104.5% | 106.0% | 104.6% | 84.0% | 115.3% | 94.3% | 100.0% | 97.8% | 97.7% | 98.8% | 93.4% | 94.3% | 97.5% | 100.3% | 95.0% | 99.3% | 95.5% | 98.5% | 104.7% | 101.5% | 96.1% | 98.2% | 92.5% | 91.9% | 97.9% | 105.1% | 112.3% | 96.5% | 100.6% | 104.2% | 95.4% | 93.2% | 106.1% | 104.3% | 105.9% | 114.5% | 121.4% | 91.6% | 101.2% | 108.1% | 91.1% | 97.6% | 91.5% |
| 2020-09-01 | 102.3% | 98.2% | 92.7% | 105.7% | 103.3% | 102.8% | 112.5% | 92.1% | 100.6% | 104.4% | 106.7% | 105.2% | 81.3% | 115.8% | 94.6% | 100.3% | 98.7% | 97.5% | 99.3% | 93.5% | 96.9% | 98.2% | 101.4% | 95.9% | 100.1% | 95.9% | 98.6% | 106.3% | 102.3% | 97.6% | 99.6% | 94.7% | 93.0% | 100.1% | 106.0% | 112.9% | 97.3% | 100.9% | 104.6% | 96.4% | 94.3% | 106.9% | 105.1% | 106.7% | 115.2% | 122.0% | 93.4% | 102.0% | 108.7% | 91.6% | 98.4% | 92.1% |
| 2020-10-01 | 102.8% | 99.0% | 95.7% | 106.8% | 104.1% | 104.1% | 113.4% | 92.6% | 101.0% | 104.4% | 107.9% | 106.1% | 84.5% | 116.9% | 95.3% | 101.2% | 99.6% | 97.8% | 99.8% | 94.7% | 97.8% | 98.7% | 102.4% | 96.8% | 101.3% | 96.7% | 99.3% | 107.2% | 102.5% | 99.2% | 99.9% | 95.5% | 93.7% | 100.8% | 107.0% | 113.2% | 97.8% | 101.4% | 105.1% | 97.0% | 95.7% | 107.8% | 106.2% | 108.1% | 116.0% | 123.4% | 93.7% | 102.5% | 109.0% | 92.3% | 98.8% | 92.3% |
| 2020-11-01 | 103.0% | 99.2% | 96.6% | 107.2% | 104.5% | 104.6% | 113.5% | 92.5% | 101.1% | 104.3% | 108.1% | 106.6% | 86.3% | 117.4% | 94.7% | 101.2% | 99.3% | 97.8% | 99.8% | 95.1% | 98.2% | 99.0% | 102.9% | 96.8% | 101.1% | 96.9% | 99.5% | 107.1% | 102.8% | 99.7% | 100.3% | 95.4% | 93.6% | 100.8% | 107.3% | 112.4% | 98.0% | 101.5% | 105.2% | 97.1% | 95.6% | 108.2% | 106.0% | 108.4% | 116.5% | 123.7% | 93.6% | 102.7% | 109.3% | 92.6% | 98.6% | 92.7% |
| 2020-12-01 | 103.0% | 99.5% | 96.8% | 107.5% | 104.2% | 103.9% | 112.4% | 92.3% | 101.0% | 104.2% | 108.6% | 107.2% | 87.7% | 118.0% | 94.6% | 101.3% | 99.7% | 98.0% | 99.6% | 95.4% | 98.2% | 99.2% | 102.8% | 95.2% | 99.5% | 97.2% | 99.6% | 107.6% | 103.2% | 99.8% | 99.2% | 95.6% | 92.3% | 100.6% | 107.9% | 112.9% | 98.0% | 101.6% | 104.2% | 96.5% | 94.5% | 108.8% | 106.0% | 109.0% | 116.9% | 124.1% | 92.1% | 102.9% | 108.6% | 92.7% | 98.8% | 93.2% |
| 2021-01-01 | 103.3% | 99.5% | 97.1% | 107.9% | 104.9% | 103.5% | 113.4% | 92.5% | 101.0% | 104.0% | 109.1% | 107.3% | 88.3% | 118.6% | 95.2% | 101.9% | 100.0% | 98.5% | 101.1% | 95.4% | 98.7% | 99.7% | 103.4% | 96.1% | 101.1% | 97.1% | 99.9% | 108.1% | 103.3% | 100.0% | 100.7% | 96.1% | 92.6% | 100.7% | 107.9% | 113.5% | 98.4% | 101.7% | 104.2% | 97.1% | 95.4% | 109.0% | 106.4% | 108.9% | 117.3% | 124.9% | 92.6% | 103.2% | 108.7% | 92.6% | 99.3% | 92.8% |
| 2021-02-01 | 103.9% | 99.7% | 96.8% | 108.3% | 104.6% | 104.9% | 114.4% | 92.8% | 101.2% | 103.9% | 109.6% | 107.7% | 88.7% | 119.2% | 95.7% | 101.7% | 99.9% | 97.9% | 100.9% | 95.3% | 99.3% | 99.7% | 103.9% | 97.4% | 101.5% | 96.8% | 99.6% | 108.4% | 103.1% | 101.1% | 100.6% | 96.5% | 93.2% | 101.0% | 108.2% | 113.6% | 98.5% | 101.0% | 105.0% | 97.5% | 96.0% | 109.3% | 106.4% | 109.1% | 116.9% | 125.5% | 93.2% | 103.3% | 109.5% | 93.1% | 99.2% | 93.3% |
| 2021-03-01 | 104.4% | 99.9% | 97.4% | 109.0% | 105.5% | 105.6% | 115.0% | 93.4% | 101.5% | 104.2% | 110.1% | 108.0% | 89.7% | 119.9% | 96.2% | 102.2% | 100.4% | 98.8% | 101.8% | 95.9% | 99.7% | 100.2% | 104.4% | 97.8% | 102.1% | 97.3% | 100.4% | 109.2% | 103.6% | 102.1% | 101.1% | 96.9% | 94.1% | 101.7% | 108.8% | 114.0% | 98.8% | 102.0% | 106.4% | 98.2% | 96.7% | 109.5% | 107.0% | 109.5% | 118.1% | 125.8% | 93.7% | 103.5% | 110.3% | 93.9% | 99.6% | 93.8% |
| 2021-04-01 | 104.6% | 99.8% | 97.0% | 109.2% | 105.6% | 106.8% | 115.7% | 93.4% | 101.8% | 104.4% | 110.6% | 108.2% | 91.7% | 120.4% | 96.4% | 102.2% | 100.3% | 98.8% | 101.4% | 96.2% | 99.8% | 100.4% | 105.0% | 97.7% | 102.4% | 97.2% | 100.4% | 109.6% | 103.6% | 103.5% | 101.6% | 97.4% | 94.4% | 102.1% | 109.1% | 114.6% | 98.9% | 102.0% | 106.9% | 98.2% | 97.0% | 109.5% | 107.4% | 109.2% | 118.7% | 126.6% | 95.3% | 103.6% | 110.9% | 93.7% | 100.0% | 94.1% |
| 2021-05-01 | 104.9% | 100.1% | 95.7% | 109.7% | 105.7% | 107.4% | 116.2% | 93.8% | 101.5% | 105.0% | 111.3% | 108.8% | 92.4% | 120.5% | 96.3% | 102.4% | 100.3% | 99.1% | 101.7% | 96.5% | 99.8% | 100.7% | 105.2% | 97.9% | 102.6% | 97.3% | 100.5% | 109.5% | 103.7% | 104.4% | 102.0% | 97.7% | 95.0% | 102.3% | 109.6% | 114.5% | 98.9% | 102.2% | 106.9% | 98.5% | 97.5% | 109.7% | 107.6% | 109.7% | 119.2% | 126.9% | 95.2% | 103.7% | 111.2% | 93.7% | 100.0% | 94.1% |
| 2021-06-01 | 105.3% | 100.4% | 95.5% | 110.4% | 105.8% | 107.7% | 116.8% | 94.1% | 101.8% | 105.7% | 112.1% | 109.2% | 93.6% | 121.0% | 96.7% | 102.7% | 100.4% | 99.2% | 101.7% | 96.4% | 99.7% | 100.5% | 105.5% | 98.3% | 102.5% | 97.4% | 100.9% | 110.2% | 104.0% | 105.4% | 102.1% | 98.1% | 95.2% | 102.7% | 110.6% | 114.7% | 99.1% | 102.6% | 107.1% | 98.8% | 97.8% | 109.7% | 107.7% | 111.0% | 119.7% | 127.6% | 95.2% | 103.8% | 111.7% | 93.7% | 100.2% | 94.2% |
| 2021-07-01 | 105.8% | 100.8% | 96.7% | 111.2% | 106.5% | 109.0% | 117.5% | 95.0% | 102.2% | 106.3% | 113.4% | 110.2% | 95.6% | 121.7% | 97.4% | 104.0% | 101.0% | 100.0% | 101.9% | 97.3% | 100.3% | 101.3% | 106.9% | 99.2% | 103.5% | 98.5% | 102.2% | 110.4% | 104.5% | 107.0% | 103.4% | 98.9% | 96.8% | 103.5% | 111.3% | 115.3% | 99.7% | 102.6% | 109.1% | 99.4% | 98.5% | 110.5% | 108.5% | 111.3% | 120.9% | 128.2% | 96.5% | 104.5% | 112.4% | 94.3% | 100.8% | 94.2% |
| 2021-08-01 | 106.2% | 100.7% | 96.9% | 111.2% | 106.8% | 109.6% | 117.7% | 94.9% | 102.2% | 106.7% | 113.5% | 110.2% | 95.0% | 122.1% | 97.4% | 103.7% | 100.9% | 99.7% | 102.7% | 97.3% | 100.4% | 101.8% | 107.2% | 99.3% | 103.3% | 98.2% | 101.9% | 110.8% | 104.4% | 107.6% | 103.6% | 99.0% | 97.0% | 103.7% | 111.1% | 115.3% | 99.8% | 102.5% | 109.0% | 99.5% | 98.3% | 110.6% | 108.5% | 111.4% | 121.2% | 128.4% | 95.8% | 105.0% | 113.0% | 94.2% | 100.6% | 94.2% |
| 2021-09-01 | 106.5% | 100.4% | 97.1% | 111.5% | 106.7% | 109.5% | 117.9% | 94.8% | 101.8% | 107.1% | 113.9% | 110.3% | 94.5% | 122.1% | 97.7% | 103.5% | 101.0% | 99.1% | 102.3% | 95.0% | 100.4% | 101.5% | 106.7% | 99.4% | 102.8% | 98.3% | 101.5% | 111.0% | 104.1% | 108.0% | 103.1% | 99.6% | 96.8% | 104.1% | 110.9% | 115.3% | 99.4% | 102.5% | 109.0% | 99.4% | 98.8% | 110.3% | 108.5% | 111.0% | 121.6% | 127.9% | 95.6% | 104.8% | 113.4% | 93.9% | 100.4% | 94.3% |
| 2021-10-01 | 106.9% | 101.1% | 99.0% | 111.7% | 107.4% | 110.0% | 118.5% | 95.3% | 102.5% | 108.5% | 114.5% | 111.1% | 94.5% | 122.3% | 98.5% | 104.1% | 101.0% | 99.0% | 102.8% | 97.0% | 100.3% | 102.2% | 107.6% | 100.2% | 103.0% | 99.4% | 101.7% | 111.2% | 104.4% | 109.5% | 103.5% | 99.8% | 97.8% | 105.0% | 111.3% | 116.0% | 99.3% | 103.0% | 109.0% | 100.0% | 98.5% | 110.7% | 108.8% | 111.8% | 122.4% | 128.7% | 96.0% | 105.2% | 113.8% | 94.4% | 100.4% | 94.9% |
| 2021-11-01 | 107.4% | 101.0% | 99.1% | 111.7% | 107.9% | 110.3% | 119.1% | 95.6% | 102.5% | 108.7% | 115.1% | 111.5% | 94.6% | 122.4% | 99.0% | 104.7% | 101.2% | 99.3% | 103.0% | 97.4% | 100.4% | 102.6% | 108.0% | 100.6% | 103.3% | 99.4% | 102.0% | 112.0% | 104.5% | 109.7% | 103.8% | 100.5% | 98.1% | 105.5% | 111.4% | 116.9% | 99.6% | 103.1% | 109.6% | 100.4% | 99.0% | 111.1% | 108.4% | 112.1% | 123.2% | 129.2% | 96.3% | 105.5% | 114.2% | 94.8% | 100.6% | 95.5% |
| 2021-12-01 | 107.8% | 101.0% | 99.3% | 112.4% | 108.2% | 110.7% | 119.4% | 95.5% | 102.8% | 109.0% | 115.2% | 112.0% | 94.8% | 122.8% | 99.3% | 105.2% | 101.8% | 99.1% | 103.4% | 97.8% | 101.0% | 102.9% | 108.5% | 100.9% | 103.4% | 99.6% | 102.6% | 112.5% | 104.5% | 110.0% | 103.9% | 100.8% | 98.3% | 106.0% | 111.8% | 116.8% | 99.7% | 103.1% | 110.0% | 100.5% | 99.4% | 111.4% | 108.4% | 112.8% | 123.5% | 129.3% | 96.5% | 105.7% | 114.7% | 95.1% | 100.8% | 95.8% |
| 2022-01-01 | 108.2% | 101.2% | 99.3% | 112.8% | 108.5% | 111.1% | 119.7% | 95.6% | 102.8% | 108.9% | 115.7% | 112.6% | 95.0% | 123.9% | 99.5% | 105.3% | 102.0% | 99.9% | 103.9% | 98.1% | 101.7% | 102.6% | 108.7% | 101.2% | 103.6% | 99.9% | 103.0% | 112.7% | 104.6% | 110.4% | 103.7% | 101.1% | 98.5% | 106.2% | 112.1% | 117.3% | 100.3% | 103.5% | 110.3% | 100.8% | 99.2% | 111.8% | 108.5% | 113.0% | 124.0% | 130.0% | 96.8% | 105.7% | 114.8% | 95.1% | 100.9% | 96.0% |
| 2022-02-01 | 108.7% | 101.6% | 99.0% | 113.2% | 108.5% | 112.0% | 120.4% | 95.9% | 103.3% | 109.1% | 116.2% | 113.3% | 95.4% | 123.8% | 99.9% | 105.7% | 102.6% | 100.4% | 104.2% | 98.3% | 102.3% | 103.2% | 109.4% | 101.5% | 104.1% | 100.1% | 103.3% | 113.0% | 105.9% | 111.0% | 104.5% | 101.8% | 99.3% | 106.6% | 112.8% | 117.6% | 100.6% | 104.2% | 110.9% | 101.3% | 100.1% | 112.8% | 108.6% | 113.6% | 124.7% | 130.7% | 97.1% | 106.3% | 115.7% | 95.5% | 101.7% | 96.8% |
| 2022-03-01 | 109.0% | 101.7% | 99.3% | 113.0% | 108.5% | 112.5% | 120.6% | 96.1% | 103.4% | 109.2% | 116.4% | 113.8% | 95.6% | 123.7% | 100.2% | 106.0% | 102.4% | 100.4% | 104.4% | 98.4% | 103.0% | 103.3% | 110.1% | 101.8% | 104.5% | 99.8% | 103.3% | 113.1% | 106.0% | 111.4% | 105.0% | 102.2% | 99.6% | 106.9% | 113.3% | 117.4% | 100.9% | 104.4% | 111.3% | 101.6% | 100.4% | 112.5% | 109.2% | 114.1% | 125.1% | 130.7% | 97.4% | 106.5% | 116.0% | 95.8% | 101.7% | 96.7% |
| 2022-04-01 | 109.3% | 101.7% | 99.3% | 113.5% | 108.5% | 112.8% | 121.3% | 96.2% | 103.6% | 109.5% | 117.1% | 114.2% | 96.1% | 124.2% | 100.3% | 106.0% | 102.6% | 100.5% | 104.6% | 98.5% | 102.7% | 103.3% | 110.3% | 101.8% | 105.0% | 99.7% | 103.1% | 113.5% | 106.2% | 111.7% | 105.6% | 102.6% | 99.8% | 107.2% | 113.4% | 117.3% | 101.0% | 104.4% | 111.5% | 101.8% | 101.0% | 112.8% | 109.7% | 114.4% | 125.7% | 131.1% | 97.2% | 106.8% | 116.6% | 96.2% | 101.9% | 96.8% |
| 2022-05-01 | 109.5% | 102.3% | 98.2% | 113.7% | 108.2% | 113.0% | 121.4% | 96.3% | 104.0% | 109.3% | 117.4% | 114.7% | 95.9% | 124.0% | 100.5% | 106.6% | 102.8% | 100.4% | 104.3% | 98.5% | 102.3% | 103.7% | 110.3% | 101.6% | 105.2% | 99.7% | 103.1% | 112.7% | 106.2% | 111.7% | 105.1% | 102.9% | 99.7% | 107.5% | 113.7% | 117.2% | 101.1% | 104.6% | 112.0% | 102.0% | 101.1% | 113.4% | 110.1% | 114.5% | 126.3% | 131.3% | 96.9% | 107.1% | 116.5% | 97.6% | 101.9% | 96.0% |
| 2022-06-01 | 109.8% | 102.4% | 97.3% | 114.2% | 108.6% | 113.3% | 121.7% | 96.5% | 104.5% | 109.3% | 118.0% | 115.0% | 96.1% | 124.7% | 100.8% | 106.3% | 103.0% | 100.7% | 104.9% | 98.5% | 101.9% | 103.9% | 110.5% | 101.7% | 105.3% | 100.0% | 103.2% | 113.8% | 106.7% | 112.5% | 105.2% | 103.1% | 99.8% | 107.8% | 114.3% | 118.1% | 101.1% | 105.1% | 112.3% | 102.4% | 101.1% | 113.8% | 109.8% | 115.7% | 127.2% | 131.6% | 97.3% | 107.2% | 116.7% | 96.4% | 101.7% | 95.9% |
| 2022-07-01 | 110.2% | 102.7% | 98.0% | 115.1% | 109.7% | 113.8% | 121.8% | 97.0% | 104.8% | 109.9% | 118.8% | 115.3% | 97.2% | 125.3% | 101.4% | 106.5% | 103.2% | 101.1% | 104.4% | 99.3% | 102.4% | 104.4% | 110.8% | 102.4% | 105.9% | 100.0% | 104.1% | 113.5% | 106.6% | 113.2% | 105.3% | 103.4% | 100.3% | 108.2% | 115.1% | 118.2% | 101.2% | 105.5% | 113.1% | 102.9% | 101.1% | 114.6% | 110.6% | 115.4% | 127.9% | 132.2% | 97.8% | 107.7% | 117.0% | 96.8% | 102.1% | 96.5% |
| 2022-08-01 | 110.4% | 102.9% | 99.0% | 115.2% | 109.9% | 114.1% | 122.4% | 97.1% | 105.2% | 109.4% | 119.1% | 115.6% | 97.4% | 125.7% | 101.4% | 106.3% | 103.6% | 101.0% | 105.9% | 99.6% | 102.6% | 104.7% | 110.8% | 102.5% | 105.9% | 99.5% | 104.0% | 113.2% | 106.3% | 112.9% | 105.1% | 103.7% | 100.4% | 108.4% | 115.4% | 118.5% | 101.3% | 105.4% | 113.6% | 103.0% | 101.5% | 115.0% | 111.1% | 115.5% | 128.1% | 132.5% | 97.7% | 108.1% | 117.8% | 96.9% | 102.4% | 96.7% |
| 2022-09-01 | 110.6% | 103.1% | 100.3% | 115.4% | 109.7% | 114.1% | 122.7% | 97.4% | 104.9% | 109.9% | 119.8% | 115.9% | 97.7% | 125.9% | 101.7% | 106.7% | 103.6% | 101.3% | 106.4% | 99.9% | 102.9% | 104.9% | 111.5% | 102.6% | 106.1% | 99.5% | 104.1% | 113.4% | 107.1% | 113.2% | 105.9% | 104.0% | 100.6% | 108.5% | 115.8% | 119.1% | 101.4% | 105.4% | 113.6% | 103.2% | 101.3% | 115.2% | 111.3% | 115.9% | 128.5% | 132.4% | 97.7% | 108.3% | 118.0% | 97.4% | 102.5% | 97.0% |
| 2022-10-01 | 111.3% | 104.6% | 100.8% | 116.1% | 112.0% | 115.4% | 122.4% | 97.5% | 108.1% | 109.7% | 120.3% | 116.1% | 99.7% | 127.1% | 101.6% | 107.6% | 103.7% | 103.6% | 106.7% | 99.5% | 103.3% | 103.8% | 111.7% | 103.0% | 106.9% | 101.0% | 104.9% | 114.9% | 106.8% | 117.5% | 106.7% | 104.5% | 100.7% | 109.5% | 116.3% | 119.1% | 102.4% | 106.7% | 113.1% | 103.9% | 101.3% | 116.2% | 111.8% | 116.7% | 129.3% | 133.7% | 98.6% | 108.6% | 119.0% | 95.8% | 103.6% | 96.9% |
| 2022-11-01 | 111.5% | 104.8% | 101.7% | 116.5% | 111.8% | 115.5% | 122.4% | 97.8% | 108.2% | 110.1% | 120.8% | 116.2% | 100.0% | 127.3% | 101.9% | 107.9% | 103.7% | 103.8% | 106.4% | 99.8% | 103.9% | 103.9% | 112.1% | 103.3% | 107.1% | 101.1% | 105.1% | 114.9% | 107.1% | 117.9% | 107.2% | 105.0% | 100.8% | 109.8% | 116.4% | 118.8% | 102.5% | 107.2% | 113.4% | 104.1% | 101.4% | 116.1% | 112.1% | 117.0% | 129.6% | 134.0% | 98.4% | 108.7% | 119.3% | 96.7% | 103.8% | 97.5% |
| 2022-12-01 | 111.7% | 105.1% | 101.9% | 116.5% | 111.7% | 115.4% | 123.0% | 97.7% | 108.2% | 110.1% | 121.3% | 116.4% | 99.7% | 127.5% | 101.8% | 107.7% | 103.8% | 104.0% | 106.3% | 99.9% | 104.2% | 104.0% | 112.2% | 103.3% | 106.8% | 101.2% | 105.1% | 115.5% | 107.4% | 118.0% | 107.2% | 105.2% | 100.8% | 110.2% | 116.6% | 118.8% | 102.5% | 107.3% | 113.7% | 104.4% | 101.3% | 116.1% | 112.0% | 117.1% | 130.0% | 134.0% | 98.7% | 108.8% | 119.6% | 95.7% | 103.7% | 97.8% |
| 2023-01-01 | 112.0% | 105.1% | 102.3% | 117.2% | 112.1% | 115.8% | 122.9% | 98.2% | 108.6% | 110.0% | 121.5% | 116.8% | 100.1% | 128.5% | 102.0% | 108.1% | 104.2% | 104.5% | 106.9% | 100.3% | 104.1% | 104.3% | 112.5% | 103.6% | 107.3% | 101.5% | 105.3% | 115.9% | 107.6% | 118.4% | 108.3% | 105.7% | 101.5% | 110.2% | 117.1% | 119.3% | 102.9% | 107.7% | 114.3% | 104.8% | 101.7% | 116.8% | 112.4% | 117.7% | 130.4% | 134.4% | 99.3% | 109.2% | 120.0% | 96.1% | 103.9% | 97.7% |
| 2023-02-01 | 112.2% | 105.2% | 102.1% | 117.4% | 112.1% | 116.0% | 123.1% | 98.5% | 109.0% | 110.3% | 122.0% | 116.9% | 100.6% | 128.7% | 102.1% | 108.3% | 104.2% | 104.1% | 107.2% | 100.4% | 104.1% | 104.3% | 112.8% | 103.9% | 107.7% | 101.5% | 105.5% | 115.9% | 107.8% | 119.0% | 108.0% | 105.6% | 101.7% | 110.5% | 117.3% | 119.7% | 103.0% | 107.6% | 114.1% | 104.9% | 102.1% | 116.9% | 112.8% | 117.8% | 130.7% | 135.2% | 99.7% | 109.4% | 120.5% | 96.3% | 104.1% | 97.9% |
| 2023-03-01 | 112.3% | 105.4% | 101.7% | 117.4% | 112.1% | 116.1% | 123.0% | 98.4% | 109.5% | 110.5% | 122.1% | 117.1% | 100.5% | 129.0% | 102.3% | 108.4% | 104.4% | 103.9% | 107.8% | 100.6% | 103.9% | 104.4% | 113.1% | 103.9% | 107.4% | 101.4% | 105.6% | 115.7% | 107.9% | 119.4% | 108.2% | 105.7% | 102.1% | 110.6% | 117.4% | 119.8% | 103.2% | 107.5% | 114.2% | 105.0% | 101.7% | 117.2% | 112.7% | 117.9% | 131.0% | 135.4% | 100.0% | 109.4% | 120.7% | 96.3% | 104.2% | 98.2% |
| 2023-04-01 | 112.5% | 105.6% | 101.9% | 117.7% | 112.4% | 116.5% | 123.2% | 98.5% | 109.7% | 110.5% | 122.4% | 117.3% | 100.4% | 128.9% | 102.4% | 108.8% | 104.7% | 104.0% | 107.8% | 101.0% | 104.0% | 104.6% | 113.3% | 104.1% | 107.6% | 101.6% | 105.7% | 115.8% | 107.8% | 119.1% | 108.0% | 105.9% | 102.0% | 110.2% | 117.6% | 119.8% | 103.5% | 107.5% | 114.2% | 105.2% | 100.9% | 117.6% | 113.0% | 117.8% | 131.3% | 135.9% | 100.3% | 109.5% | 120.8% | 96.2% | 104.3% | 98.0% |
| 2023-05-01 | 112.7% | 105.8% | 101.9% | 117.7% | 112.9% | 116.8% | 123.6% | 98.8% | 110.2% | 111.0% | 122.5% | 117.6% | 100.3% | 129.2% | 102.5% | 109.0% | 104.6% | 103.9% | 108.1% | 101.2% | 104.0% | 104.7% | 113.5% | 104.4% | 107.8% | 101.3% | 106.0% | 115.4% | 107.6% | 119.4% | 108.5% | 106.2% | 102.2% | 110.5% | 117.8% | 120.1% | 103.7% | 107.6% | 114.5% | 105.4% | 100.7% | 117.9% | 113.0% | 118.0% | 131.7% | 136.4% | 99.6% | 109.6% | 121.0% | 96.3% | 104.2% | 98.7% |
| 2023-06-01 | 112.8% | 106.1% | 101.8% | 117.8% | 113.1% | 116.8% | 123.7% | 98.6% | 110.2% | 111.2% | 122.6% | 117.6% | 100.3% | 129.6% | 102.7% | 108.7% | 104.3% | 104.1% | 108.4% | 101.1% | 104.0% | 104.7% | 113.6% | 104.4% | 107.7% | 101.1% | 106.5% | 115.8% | 108.1% | 119.8% | 107.9% | 106.1% | 102.7% | 110.6% | 118.1% | 120.6% | 103.8% | 107.8% | 114.8% | 105.5% | 100.9% | 118.2% | 112.9% | 118.3% | 132.0% | 136.4% | 98.9% | 109.7% | 121.4% | 96.5% | 104.3% | 99.2% |
| 2023-07-01 | 113.0% | 106.3% | 101.8% | 117.8% | 113.1% | 117.0% | 123.7% | 98.8% | 109.6% | 110.8% | 123.2% | 117.6% | 101.1% | 129.9% | 102.8% | 109.1% | 103.9% | 104.2% | 108.4% | 101.0% | 103.6% | 104.8% | 114.0% | 104.4% | 107.7% | 101.1% | 106.7% | 115.2% | 108.1% | 119.9% | 107.8% | 106.1% | 102.6% | 110.6% | 118.4% | 121.0% | 104.1% | 108.0% | 115.2% | 105.8% | 100.6% | 118.3% | 113.0% | 118.5% | 132.2% | 136.3% | 99.8% | 109.7% | 121.2% | 96.5% | 104.5% | 98.8% |
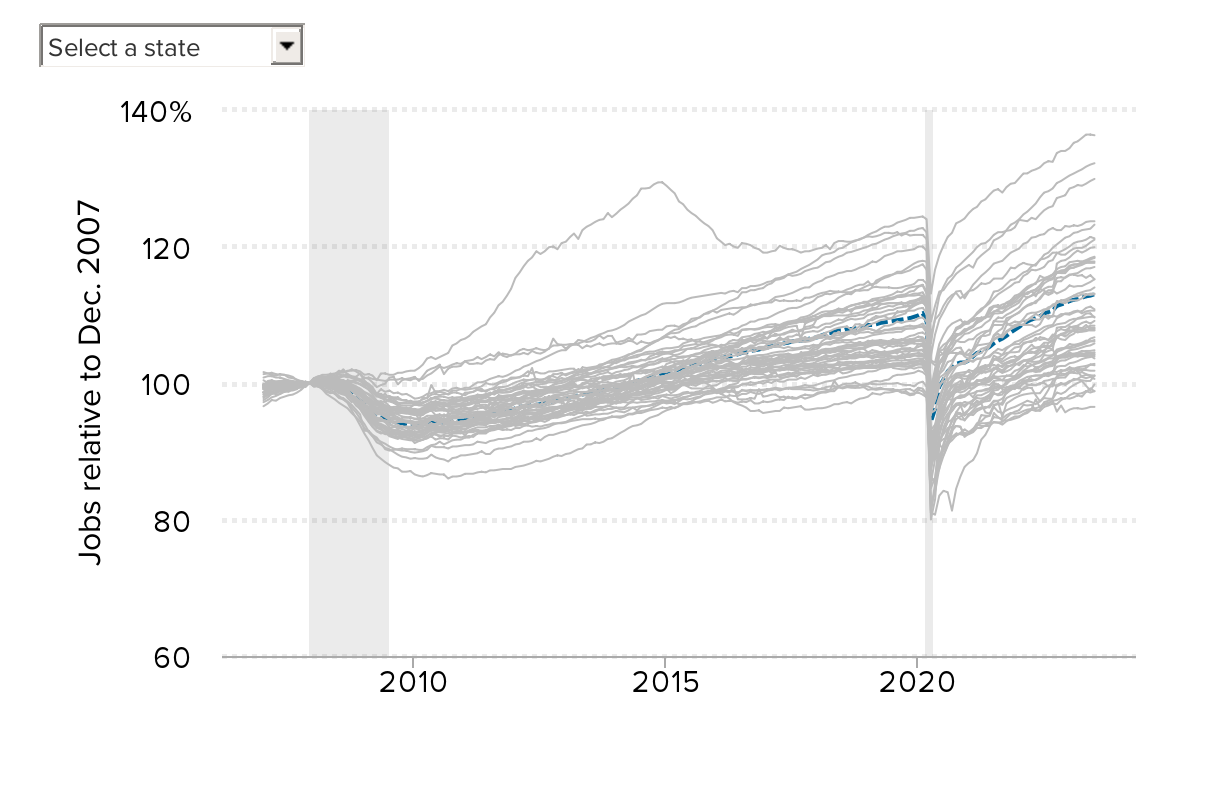
Notes: Shaded areas represent recessions. Values are indexed to December 2007, the month that the Great Recession began.
Source: EPI/EARN analysis of Bureau of Labor Statistics Local Area Unemployment Statistics data.
State labor force level relative to January 2007: Choose a state to show the change in the labor force over time for that state and all other states in the same Census division. (The dashed line shows values for the U.S.)
| date | United States | Alabama | Alaska | Arizona | Arkansas | California | Colorado | Connecticut | Delaware | District of Columbia | Florida | Georgia | Hawaii | Idaho | Illinois | Indiana | Iowa | Kansas | Kentucky | Louisiana | Maine | Maryland | Massachusetts | Michigan | Minnesota | Mississippi | Missouri | Montana | Nebraska | Nevada | New Hampshire | New Jersey | New Mexico | New York | North Carolina | North Dakota | Ohio | Oklahoma | Oregon | Pennsylvania | Rhode Island | South Carolina | South Dakota | Tennessee | Texas | Utah | Vermont | Virginia | Washington | West Virginia | Wisconsin | Wyoming |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007-01-01 | 99.5% | 100.2% | 99.4% | 99.2% | 99.8% | 98.8% | 97.7% | 98.9% | 99.2% | 98.4% | 99.1% | 98.5% | 100.1% | 99.6% | 98.3% | 100.3% | 99.6% | 99.8% | 101.0% | 99.0% | 100.4% | 99.7% | 99.8% | 101.2% | 100.3% | 99.2% | 99.7% | 98.2% | 99.2% | 97.5% | 99.7% | 99.5% | 99.2% | 99.3% | 99.4% | 99.4% | 100.0% | 100.0% | 99.1% | 99.1% | 100.4% | 101.5% | 99.8% | 100.1% | 99.0% | 98.2% | 101.1% | 98.4% | 98.0% | 99.8% | 99.8% | 98.4% |
| 2007-02-01 | 99.4% | 100.1% | 99.3% | 99.2% | 99.9% | 98.9% | 97.7% | 99.0% | 99.2% | 98.5% | 99.3% | 98.5% | 100.0% | 99.7% | 98.3% | 100.0% | 99.5% | 99.8% | 100.9% | 99.1% | 100.2% | 99.5% | 99.8% | 101.0% | 100.3% | 99.1% | 99.7% | 98.4% | 99.1% | 97.8% | 99.7% | 99.4% | 99.2% | 99.2% | 99.3% | 99.4% | 100.0% | 100.1% | 99.1% | 99.0% | 100.3% | 101.4% | 99.8% | 100.0% | 99.0% | 98.4% | 100.9% | 98.5% | 98.1% | 99.6% | 99.8% | 98.4% |
| 2007-03-01 | 99.4% | 100.0% | 99.2% | 99.2% | 99.8% | 98.9% | 97.7% | 99.1% | 99.1% | 98.4% | 99.3% | 98.6% | 99.9% | 99.8% | 98.3% | 99.7% | 99.4% | 99.7% | 100.7% | 99.1% | 100.0% | 99.4% | 99.8% | 100.8% | 100.2% | 99.0% | 99.6% | 98.6% | 99.1% | 98.0% | 99.7% | 99.2% | 99.1% | 99.2% | 99.3% | 99.4% | 100.0% | 100.0% | 99.0% | 99.0% | 100.2% | 101.2% | 99.7% | 99.8% | 98.9% | 98.6% | 100.8% | 98.5% | 98.2% | 99.4% | 99.8% | 98.5% |
| 2007-04-01 | 99.0% | 99.8% | 99.2% | 99.1% | 99.7% | 99.0% | 97.8% | 99.1% | 99.1% | 98.4% | 99.4% | 98.6% | 99.7% | 99.9% | 98.4% | 99.4% | 99.3% | 99.6% | 100.5% | 99.0% | 99.8% | 99.2% | 99.8% | 100.6% | 100.1% | 98.9% | 99.6% | 98.7% | 99.2% | 98.2% | 99.7% | 99.2% | 99.1% | 99.1% | 99.2% | 99.3% | 100.0% | 99.9% | 99.0% | 99.0% | 100.0% | 101.0% | 99.7% | 99.7% | 98.9% | 98.8% | 100.6% | 98.5% | 98.3% | 99.3% | 99.7% | 98.6% |
| 2007-05-01 | 99.2% | 99.7% | 99.1% | 99.0% | 99.7% | 99.1% | 98.0% | 99.2% | 99.0% | 98.3% | 99.4% | 98.7% | 99.5% | 100.0% | 98.6% | 99.2% | 99.3% | 99.6% | 100.3% | 98.9% | 99.6% | 99.2% | 99.7% | 100.5% | 100.0% | 98.9% | 99.6% | 98.8% | 99.3% | 98.4% | 99.6% | 99.1% | 99.0% | 99.1% | 99.3% | 99.3% | 100.0% | 99.8% | 99.0% | 99.0% | 100.0% | 100.7% | 99.7% | 99.6% | 98.9% | 98.9% | 100.4% | 98.6% | 98.5% | 99.3% | 99.7% | 98.8% |
| 2007-06-01 | 99.4% | 99.7% | 99.2% | 99.0% | 99.7% | 99.2% | 98.3% | 99.2% | 99.0% | 98.3% | 99.4% | 98.8% | 99.4% | 100.2% | 98.8% | 99.0% | 99.3% | 99.6% | 100.2% | 98.9% | 99.5% | 99.2% | 99.7% | 100.4% | 100.0% | 98.9% | 99.6% | 99.0% | 99.4% | 98.6% | 99.6% | 99.2% | 99.0% | 99.2% | 99.4% | 99.3% | 100.0% | 99.7% | 99.0% | 99.1% | 99.9% | 100.5% | 99.7% | 99.5% | 99.0% | 99.1% | 100.3% | 98.7% | 98.6% | 99.4% | 99.8% | 98.9% |
| 2007-07-01 | 99.4% | 99.7% | 99.3% | 99.0% | 99.7% | 99.3% | 98.6% | 99.3% | 99.1% | 98.4% | 99.4% | 99.0% | 99.3% | 100.3% | 99.1% | 99.0% | 99.4% | 99.7% | 100.1% | 98.9% | 99.5% | 99.3% | 99.7% | 100.4% | 100.0% | 99.0% | 99.7% | 99.2% | 99.5% | 98.8% | 99.6% | 99.2% | 99.1% | 99.3% | 99.5% | 99.3% | 100.0% | 99.7% | 99.1% | 99.2% | 99.9% | 100.4% | 99.7% | 99.6% | 99.0% | 99.2% | 100.2% | 98.9% | 98.8% | 99.5% | 99.8% | 99.1% |
| 2007-08-01 | 99.2% | 99.8% | 99.4% | 99.1% | 99.7% | 99.5% | 98.9% | 99.4% | 99.2% | 98.7% | 99.5% | 99.2% | 99.3% | 100.4% | 99.3% | 99.1% | 99.5% | 99.8% | 100.1% | 99.0% | 99.6% | 99.5% | 99.7% | 100.3% | 100.0% | 99.2% | 99.8% | 99.3% | 99.6% | 99.0% | 99.6% | 99.3% | 99.2% | 99.4% | 99.6% | 99.4% | 100.0% | 99.7% | 99.3% | 99.4% | 99.9% | 100.3% | 99.8% | 99.7% | 99.2% | 99.4% | 100.1% | 99.1% | 99.1% | 99.7% | 99.9% | 99.3% |
| 2007-09-01 | 99.7% | 99.8% | 99.6% | 99.3% | 99.8% | 99.6% | 99.3% | 99.6% | 99.3% | 99.0% | 99.6% | 99.4% | 99.4% | 100.4% | 99.5% | 99.3% | 99.6% | 99.9% | 100.1% | 99.2% | 99.7% | 99.6% | 99.8% | 100.3% | 100.0% | 99.4% | 99.9% | 99.5% | 99.7% | 99.3% | 99.7% | 99.5% | 99.3% | 99.6% | 99.8% | 99.5% | 100.0% | 99.8% | 99.5% | 99.6% | 100.0% | 100.2% | 99.9% | 99.8% | 99.4% | 99.6% | 100.0% | 99.3% | 99.3% | 99.8% | 99.9% | 99.4% |
| 2007-10-01 | 99.5% | 99.9% | 99.8% | 99.5% | 99.9% | 99.8% | 99.6% | 99.7% | 99.5% | 99.4% | 99.7% | 99.6% | 99.5% | 100.4% | 99.7% | 99.6% | 99.7% | 100.0% | 100.1% | 99.5% | 99.8% | 99.8% | 99.8% | 100.3% | 100.0% | 99.7% | 100.0% | 99.7% | 99.8% | 99.6% | 99.8% | 99.6% | 99.6% | 99.7% | 99.9% | 99.7% | 100.0% | 99.9% | 99.7% | 99.7% | 100.1% | 100.1% | 99.9% | 99.9% | 99.6% | 99.8% | 100.0% | 99.5% | 99.6% | 100.0% | 100.0% | 99.6% |
| 2007-11-01 | 99.9% | 100.0% | 99.9% | 99.7% | 100.0% | 99.9% | 99.8% | 99.9% | 99.8% | 99.7% | 99.9% | 99.8% | 99.8% | 100.2% | 99.9% | 99.8% | 99.9% | 100.0% | 100.1% | 99.8% | 99.9% | 99.9% | 99.9% | 100.2% | 100.0% | 99.9% | 100.0% | 99.8% | 99.9% | 99.8% | 99.9% | 99.8% | 99.8% | 99.9% | 100.0% | 99.8% | 100.0% | 100.0% | 99.9% | 99.9% | 100.1% | 100.0% | 100.0% | 100.0% | 99.8% | 99.9% | 100.0% | 99.8% | 99.8% | 100.0% | 100.0% | 99.8% |
| 2007-12-01 | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| 2008-01-01 | 100.1% | 100.0% | 100.1% | 100.2% | 100.0% | 100.1% | 100.1% | 100.1% | 100.2% | 100.2% | 100.1% | 100.2% | 100.2% | 99.8% | 100.1% | 100.1% | 100.1% | 100.0% | 99.9% | 100.2% | 100.0% | 100.1% | 100.1% | 99.8% | 100.0% | 100.0% | 100.0% | 100.1% | 100.1% | 100.2% | 100.1% | 100.2% | 100.2% | 100.1% | 100.0% | 100.1% | 100.0% | 100.1% | 100.1% | 100.1% | 99.9% | 100.0% | 100.0% | 100.0% | 100.2% | 100.1% | 100.0% | 100.2% | 100.2% | 100.0% | 100.0% | 100.2% |
| 2008-02-01 | 99.8% | 100.0% | 100.3% | 100.4% | 100.0% | 100.2% | 100.2% | 100.2% | 100.4% | 100.3% | 100.1% | 100.4% | 100.4% | 99.6% | 100.1% | 100.3% | 100.1% | 100.0% | 99.9% | 100.3% | 100.1% | 100.2% | 100.1% | 99.6% | 100.0% | 100.0% | 99.9% | 100.2% | 100.1% | 100.3% | 100.2% | 100.3% | 100.3% | 100.2% | 100.0% | 100.3% | 99.9% | 100.1% | 100.1% | 100.2% | 99.7% | 100.0% | 100.0% | 100.0% | 100.3% | 100.1% | 100.1% | 100.4% | 100.3% | 99.9% | 100.0% | 100.3% |
| 2008-03-01 | 100.0% | 99.9% | 100.5% | 100.7% | 100.0% | 100.3% | 100.2% | 100.2% | 100.4% | 100.5% | 100.1% | 100.7% | 100.6% | 99.5% | 100.0% | 100.4% | 100.2% | 100.0% | 99.9% | 100.4% | 100.1% | 100.4% | 100.2% | 99.5% | 100.1% | 99.9% | 99.9% | 100.3% | 100.2% | 100.5% | 100.3% | 100.3% | 100.4% | 100.2% | 100.0% | 100.4% | 99.9% | 100.2% | 100.1% | 100.3% | 99.6% | 100.1% | 100.1% | 100.1% | 100.5% | 100.0% | 100.1% | 100.6% | 100.5% | 99.9% | 100.0% | 100.5% |
| 2008-04-01 | 99.9% | 99.9% | 100.7% | 101.0% | 100.1% | 100.4% | 100.2% | 100.3% | 100.5% | 100.8% | 100.1% | 100.9% | 100.7% | 100.3% | 99.8% | 100.5% | 100.3% | 100.0% | 100.0% | 100.5% | 100.2% | 100.5% | 100.3% | 99.3% | 100.2% | 99.8% | 99.9% | 100.3% | 100.3% | 100.6% | 100.4% | 100.4% | 100.4% | 100.3% | 100.0% | 100.5% | 99.8% | 100.4% | 100.3% | 100.5% | 99.5% | 100.3% | 100.1% | 100.1% | 100.7% | 100.0% | 100.2% | 100.9% | 100.6% | 99.8% | 100.0% | 100.6% |
| 2008-05-01 | 100.3% | 99.8% | 100.9% | 101.3% | 100.2% | 100.5% | 100.3% | 100.4% | 100.5% | 101.1% | 100.1% | 101.2% | 100.7% | 100.7% | 99.6% | 100.7% | 100.5% | 100.1% | 100.2% | 100.7% | 100.3% | 100.7% | 100.5% | 99.2% | 100.3% | 99.6% | 100.0% | 100.4% | 100.3% | 100.8% | 100.4% | 100.5% | 100.5% | 100.5% | 100.1% | 100.7% | 99.9% | 100.5% | 100.5% | 100.6% | 99.5% | 100.5% | 100.2% | 100.2% | 100.9% | 99.9% | 100.3% | 101.1% | 100.9% | 99.8% | 100.0% | 100.8% |
| 2008-06-01 | 100.3% | 99.8% | 101.1% | 101.7% | 100.3% | 100.7% | 100.3% | 100.5% | 100.6% | 101.5% | 100.1% | 101.5% | 100.7% | 101.0% | 99.4% | 101.0% | 100.7% | 100.2% | 100.4% | 101.0% | 100.4% | 100.8% | 100.7% | 99.0% | 100.5% | 99.5% | 100.0% | 100.5% | 100.4% | 100.9% | 100.5% | 100.6% | 100.7% | 100.6% | 100.3% | 100.8% | 99.9% | 100.8% | 100.9% | 100.8% | 99.5% | 100.8% | 100.3% | 100.4% | 101.2% | 99.9% | 100.4% | 101.3% | 101.1% | 99.8% | 100.0% | 101.0% |
| 2008-07-01 | 100.4% | 99.7% | 101.2% | 102.0% | 100.5% | 100.9% | 100.4% | 100.6% | 100.6% | 101.7% | 100.1% | 101.7% | 100.6% | 101.2% | 99.1% | 101.1% | 100.9% | 100.3% | 100.6% | 101.3% | 100.4% | 100.9% | 100.9% | 98.9% | 100.7% | 99.3% | 100.0% | 100.6% | 100.4% | 101.0% | 100.6% | 100.8% | 100.9% | 100.9% | 100.4% | 100.9% | 100.0% | 101.0% | 101.3% | 100.9% | 99.5% | 101.0% | 100.5% | 100.5% | 101.4% | 99.8% | 100.5% | 101.5% | 101.3% | 99.8% | 100.1% | 101.2% |
| 2008-08-01 | 100.5% | 99.7% | 101.2% | 102.4% | 100.6% | 101.1% | 100.4% | 100.7% | 100.5% | 101.9% | 100.1% | 102.0% | 100.5% | 101.2% | 98.9% | 101.3% | 101.1% | 100.4% | 100.7% | 101.5% | 100.3% | 101.0% | 101.1% | 98.7% | 100.9% | 99.1% | 100.0% | 100.8% | 100.4% | 101.1% | 100.6% | 101.0% | 101.0% | 101.0% | 100.6% | 100.9% | 99.9% | 101.2% | 101.7% | 101.1% | 99.5% | 101.2% | 100.6% | 100.6% | 101.7% | 99.6% | 100.6% | 101.6% | 101.4% | 99.8% | 100.2% | 101.4% |
| 2008-09-01 | 100.4% | 99.6% | 101.2% | 102.7% | 100.6% | 101.2% | 100.4% | 100.8% | 100.5% | 101.9% | 100.0% | 98.8% | 100.3% | 101.3% | 98.6% | 101.3% | 101.2% | 100.5% | 100.8% | 101.7% | 100.2% | 101.1% | 101.2% | 98.5% | 101.0% | 98.8% | 100.0% | 100.8% | 100.5% | 101.1% | 100.5% | 101.1% | 101.1% | 101.2% | 100.6% | 100.9% | 99.8% | 101.4% | 102.0% | 101.2% | 99.5% | 101.4% | 100.7% | 100.7% | 101.9% | 99.4% | 100.6% | 101.6% | 101.4% | 99.8% | 100.4% | 101.5% |
| 2008-10-01 | 100.6% | 99.5% | 101.2% | 102.9% | 100.6% | 101.4% | 100.4% | 100.8% | 100.4% | 101.9% | 99.8% | 98.1% | 100.1% | 101.3% | 98.5% | 101.3% | 101.3% | 100.7% | 101.0% | 101.8% | 100.1% | 101.2% | 101.3% | 98.3% | 101.2% | 98.6% | 100.1% | 100.8% | 100.5% | 101.2% | 100.4% | 101.1% | 101.1% | 101.3% | 100.6% | 100.8% | 99.6% | 101.6% | 102.2% | 101.2% | 99.5% | 101.5% | 100.8% | 100.7% | 102.1% | 99.1% | 100.9% | 101.6% | 101.4% | 99.9% | 100.5% | 101.5% |
| 2008-11-01 | 100.5% | 99.5% | 101.3% | 103.0% | 100.6% | 101.5% | 100.5% | 100.9% | 100.2% | 101.8% | 99.5% | 98.0% | 99.9% | 101.3% | 98.3% | 101.3% | 101.3% | 100.9% | 101.2% | 101.8% | 100.0% | 101.3% | 101.3% | 98.1% | 101.2% | 98.5% | 100.1% | 100.6% | 100.5% | 101.2% | 100.4% | 101.2% | 101.0% | 101.4% | 102.4% | 100.7% | 99.4% | 101.7% | 102.3% | 101.3% | 99.6% | 101.6% | 100.9% | 100.7% | 102.2% | 98.7% | 101.2% | 101.6% | 101.4% | 100.0% | 100.7% | 101.5% |
| 2008-12-01 | 100.5% | 99.5% | 101.4% | 103.1% | 100.5% | 101.6% | 100.5% | 100.9% | 100.0% | 101.7% | 99.2% | 98.2% | 99.7% | 101.4% | 98.3% | 101.2% | 101.2% | 101.0% | 101.4% | 101.7% | 99.9% | 101.5% | 101.2% | 97.9% | 101.3% | 98.3% | 100.2% | 100.3% | 100.5% | 101.2% | 100.3% | 101.2% | 100.9% | 101.5% | 102.8% | 100.6% | 99.2% | 101.9% | 102.4% | 101.3% | 99.7% | 101.7% | 101.0% | 100.5% | 102.3% | 99.9% | 101.4% | 101.6% | 101.3% | 100.2% | 100.8% | 101.5% |
| 2009-01-01 | 100.2% | 99.4% | 101.5% | 103.1% | 100.5% | 101.7% | 100.6% | 100.9% | 99.7% | 101.6% | 98.8% | 98.4% | 99.4% | 101.3% | 98.3% | 101.2% | 101.1% | 101.2% | 101.7% | 101.6% | 99.9% | 101.6% | 101.2% | 98.1% | 101.3% | 98.2% | 100.2% | 100.0% | 100.5% | 101.2% | 100.2% | 101.3% | 100.7% | 101.6% | 102.7% | 100.4% | 99.0% | 102.1% | 102.5% | 101.2% | 99.9% | 101.7% | 101.1% | 100.3% | 102.3% | 100.2% | 101.6% | 101.5% | 101.2% | 100.4% | 101.0% | 101.6% |
| 2009-02-01 | 100.4% | 99.4% | 101.7% | 103.1% | 100.5% | 101.8% | 100.6% | 100.9% | 99.4% | 101.6% | 98.5% | 98.6% | 99.2% | 101.2% | 98.3% | 101.2% | 101.0% | 101.5% | 101.9% | 101.5% | 99.9% | 101.7% | 101.1% | 98.3% | 101.4% | 98.1% | 100.3% | 99.6% | 100.4% | 101.1% | 100.2% | 101.4% | 100.6% | 101.7% | 102.4% | 100.2% | 98.8% | 102.3% | 102.6% | 101.1% | 100.1% | 101.7% | 101.1% | 100.0% | 102.3% | 100.1% | 101.8% | 101.5% | 101.0% | 100.6% | 101.1% | 101.8% |
| 2009-03-01 | 100.1% | 99.4% | 101.9% | 103.1% | 100.5% | 101.8% | 100.7% | 101.0% | 99.1% | 101.7% | 98.2% | 98.8% | 99.0% | 101.1% | 98.4% | 101.1% | 100.9% | 101.7% | 102.1% | 101.4% | 99.9% | 101.7% | 101.1% | 98.4% | 101.4% | 98.0% | 100.3% | 99.3% | 100.4% | 101.0% | 100.2% | 101.5% | 100.5% | 100.9% | 102.2% | 100.1% | 98.6% | 102.6% | 102.7% | 101.0% | 100.3% | 101.7% | 101.2% | 99.7% | 102.3% | 99.9% | 102.1% | 101.5% | 100.8% | 100.8% | 101.2% | 102.1% |
| 2009-04-01 | 100.4% | 99.3% | 102.1% | 103.1% | 100.4% | 101.8% | 100.8% | 101.0% | 98.8% | 101.8% | 98.0% | 98.9% | 98.9% | 100.9% | 98.6% | 101.0% | 100.7% | 101.9% | 102.3% | 101.4% | 99.9% | 101.8% | 101.1% | 98.6% | 101.5% | 97.9% | 100.3% | 99.0% | 100.5% | 100.9% | 100.2% | 101.7% | 100.5% | 101.0% | 101.9% | 100.1% | 98.4% | 102.9% | 102.8% | 100.9% | 100.4% | 101.6% | 101.2% | 99.5% | 102.4% | 99.6% | 102.2% | 101.5% | 100.8% | 101.0% | 101.3% | 102.3% |
| 2009-05-01 | 100.5% | 99.2% | 102.2% | 103.1% | 100.3% | 101.8% | 100.7% | 101.1% | 98.4% | 101.9% | 98.2% | 99.0% | 98.9% | 101.4% | 98.7% | 100.7% | 100.6% | 102.1% | 102.3% | 101.5% | 99.8% | 101.8% | 101.1% | 98.7% | 101.5% | 97.7% | 100.3% | 98.8% | 100.5% | 100.8% | 100.1% | 101.8% | 100.5% | 101.1% | 101.7% | 100.1% | 98.2% | 103.1% | 102.7% | 100.7% | 100.4% | 101.5% | 101.3% | 99.3% | 103.5% | 99.4% | 102.6% | 101.5% | 100.7% | 101.1% | 101.3% | 102.5% |
| 2009-06-01 | 100.5% | 99.0% | 102.3% | 103.1% | 100.2% | 101.7% | 100.6% | 101.2% | 98.0% | 102.1% | 98.2% | 99.0% | 98.9% | 101.5% | 98.7% | 100.4% | 100.5% | 102.2% | 102.2% | 101.4% | 99.7% | 101.7% | 101.1% | 98.7% | 101.4% | 97.4% | 100.2% | 98.6% | 100.6% | 100.6% | 100.0% | 101.9% | 100.4% | 101.1% | 101.2% | 100.1% | 98.1% | 103.1% | 102.5% | 100.5% | 100.4% | 101.4% | 101.2% | 99.2% | 104.1% | 99.1% | 102.5% | 101.5% | 100.7% | 101.0% | 101.1% | 102.5% |
| 2009-07-01 | 100.4% | 98.8% | 102.4% | 103.1% | 100.0% | 101.6% | 100.3% | 101.3% | 97.5% | 102.4% | 98.1% | 99.0% | 98.8% | 101.4% | 98.7% | 100.0% | 100.4% | 102.1% | 102.1% | 101.3% | 99.5% | 101.6% | 101.0% | 98.2% | 101.3% | 97.2% | 100.1% | 98.4% | 100.5% | 100.5% | 99.9% | 101.9% | 100.2% | 101.1% | 101.0% | 100.2% | 98.0% | 103.0% | 102.3% | 100.2% | 100.3% | 101.2% | 101.1% | 99.1% | 104.3% | 98.8% | 102.4% | 101.4% | 100.6% | 100.9% | 100.9% | 102.3% |
| 2009-08-01 | 100.3% | 98.6% | 102.3% | 103.0% | 99.8% | 101.5% | 100.0% | 101.3% | 97.1% | 102.6% | 98.0% | 98.8% | 98.8% | 101.3% | 98.6% | 99.5% | 100.3% | 101.9% | 101.8% | 101.2% | 99.4% | 101.5% | 100.8% | 97.7% | 101.2% | 96.9% | 99.9% | 98.2% | 100.4% | 100.3% | 99.8% | 101.9% | 100.0% | 101.0% | 100.9% | 100.2% | 97.9% | 102.8% | 102.0% | 99.9% | 100.1% | 100.9% | 100.9% | 99.1% | 104.4% | 98.5% | 102.2% | 101.3% | 100.6% | 100.6% | 100.6% | 102.1% |
| 2009-09-01 | 99.9% | 98.3% | 102.2% | 102.8% | 99.6% | 101.3% | 99.7% | 101.2% | 96.6% | 102.8% | 98.0% | 98.7% | 98.7% | 101.1% | 98.4% | 99.1% | 100.1% | 101.6% | 101.5% | 101.0% | 99.2% | 101.4% | 100.7% | 97.2% | 101.0% | 96.7% | 99.6% | 98.0% | 100.3% | 100.0% | 99.7% | 101.9% | 99.8% | 100.8% | 100.7% | 100.2% | 97.8% | 102.5% | 101.8% | 99.5% | 99.9% | 100.7% | 100.8% | 99.1% | 104.4% | 98.2% | 102.0% | 101.2% | 100.6% | 100.3% | 100.2% | 102.0% |
| 2009-10-01 | 99.9% | 98.1% | 102.2% | 102.6% | 99.4% | 101.2% | 99.5% | 101.1% | 96.3% | 102.9% | 97.9% | 98.5% | 98.7% | 101.0% | 98.3% | 98.7% | 99.9% | 101.4% | 101.3% | 100.9% | 99.1% | 101.2% | 100.6% | 96.8% | 100.9% | 96.7% | 99.4% | 97.9% | 100.2% | 99.8% | 99.7% | 101.8% | 99.6% | 100.7% | 100.7% | 100.2% | 97.7% | 102.3% | 101.7% | 99.2% | 99.8% | 100.5% | 100.6% | 99.2% | 104.4% | 97.9% | 101.9% | 101.2% | 100.4% | 100.0% | 99.9% | 102.0% |
| 2009-11-01 | 100.0% | 98.0% | 102.1% | 102.5% | 99.3% | 101.1% | 99.3% | 101.1% | 96.0% | 103.0% | 98.0% | 98.4% | 98.7% | 100.9% | 98.3% | 98.5% | 99.8% | 101.1% | 101.2% | 100.8% | 99.1% | 101.2% | 100.6% | 96.5% | 100.9% | 96.7% | 99.3% | 97.9% | 100.2% | 99.7% | 99.7% | 101.9% | 99.5% | 100.7% | 100.7% | 100.3% | 97.7% | 102.2% | 101.7% | 99.0% | 99.7% | 100.5% | 100.6% | 99.4% | 104.5% | 97.7% | 101.8% | 101.2% | 100.3% | 99.9% | 99.7% | 102.2% |
| 2009-12-01 | 99.5% | 98.1% | 102.2% | 102.4% | 99.2% | 101.2% | 99.3% | 101.1% | 95.9% | 103.2% | 98.1% | 98.3% | 98.9% | 101.0% | 98.5% | 98.4% | 99.8% | 101.0% | 101.2% | 100.9% | 99.2% | 101.3% | 100.6% | 96.3% | 100.9% | 96.9% | 99.2% | 98.0% | 100.2% | 99.7% | 99.7% | 102.0% | 99.5% | 100.7% | 101.0% | 100.6% | 97.8% | 102.1% | 102.0% | 99.1% | 99.8% | 100.5% | 100.6% | 99.6% | 104.7% | 97.5% | 101.8% | 101.3% | 100.3% | 99.9% | 99.7% | 102.4% |
| 2010-01-01 | 99.7% | 98.2% | 102.4% | 102.4% | 99.3% | 101.4% | 99.5% | 101.3% | 96.0% | 103.5% | 98.4% | 98.4% | 99.3% | 101.1% | 98.7% | 98.5% | 99.9% | 100.9% | 101.4% | 101.1% | 99.3% | 101.5% | 100.8% | 96.3% | 101.1% | 97.1% | 99.3% | 98.1% | 100.3% | 99.8% | 99.8% | 102.1% | 99.7% | 100.8% | 101.3% | 100.9% | 98.0% | 102.2% | 102.3% | 99.2% | 100.0% | 100.7% | 100.7% | 100.0% | 105.0% | 97.5% | 102.0% | 101.4% | 100.4% | 100.0% | 99.8% | 102.6% |
| 2010-02-01 | 99.9% | 98.3% | 102.5% | 102.5% | 99.4% | 101.6% | 99.6% | 101.6% | 96.1% | 104.0% | 98.7% | 97.3% | 99.7% | 101.2% | 98.9% | 98.6% | 100.1% | 100.9% | 101.6% | 101.4% | 99.5% | 101.8% | 101.0% | 96.2% | 101.3% | 97.4% | 99.3% | 98.3% | 100.5% | 99.9% | 99.9% | 102.3% | 100.0% | 100.9% | 101.7% | 101.4% | 98.1% | 102.3% | 102.8% | 99.4% | 100.2% | 100.9% | 100.9% | 100.5% | 105.4% | 97.5% | 102.1% | 101.6% | 100.5% | 100.2% | 99.9% | 102.8% |
| 2010-03-01 | 100.0% | 98.3% | 102.6% | 102.5% | 99.6% | 101.8% | 99.7% | 101.8% | 96.4% | 104.4% | 99.0% | 97.0% | 100.2% | 101.2% | 98.9% | 98.7% | 100.3% | 100.9% | 101.7% | 101.7% | 99.6% | 102.0% | 101.1% | 96.2% | 101.4% | 97.6% | 99.3% | 98.4% | 100.6% | 99.9% | 100.0% | 102.3% | 100.2% | 101.0% | 102.0% | 101.8% | 98.1% | 102.4% | 103.1% | 99.5% | 100.3% | 101.1% | 101.1% | 100.9% | 105.7% | 97.5% | 102.2% | 101.8% | 100.6% | 100.4% | 99.9% | 102.9% |
| 2010-04-01 | 100.5% | 100.7% | 102.7% | 102.4% | 99.9% | 101.9% | 99.7% | 102.1% | 96.7% | 104.8% | 99.4% | 96.8% | 100.7% | 101.2% | 98.9% | 98.9% | 100.5% | 100.8% | 101.7% | 102.0% | 99.6% | 102.3% | 101.2% | 96.2% | 101.5% | 97.7% | 99.3% | 98.5% | 100.7% | 99.9% | 100.0% | 102.4% | 100.5% | 101.1% | 102.1% | 102.2% | 98.1% | 102.4% | 103.4% | 99.6% | 100.4% | 101.3% | 101.3% | 101.2% | 106.0% | 97.4% | 102.3% | 101.9% | 100.7% | 100.4% | 99.9% | 102.9% |
| 2010-05-01 | 100.1% | 101.3% | 102.7% | 102.2% | 100.1% | 102.0% | 99.7% | 102.3% | 97.0% | 105.1% | 99.7% | 96.7% | 101.2% | 101.2% | 98.8% | 98.9% | 100.5% | 100.8% | 101.7% | 102.2% | 99.6% | 102.4% | 101.2% | 96.2% | 101.6% | 97.8% | 99.3% | 98.5% | 100.8% | 99.9% | 100.1% | 102.3% | 100.6% | 101.0% | 102.1% | 102.5% | 97.9% | 102.4% | 103.5% | 99.6% | 100.4% | 101.4% | 101.5% | 101.5% | 106.2% | 97.4% | 102.3% | 102.0% | 100.6% | 100.5% | 99.8% | 102.8% |
| 2010-06-01 | 99.8% | 101.5% | 102.6% | 102.0% | 100.3% | 102.0% | 99.6% | 102.5% | 97.3% | 105.3% | 99.9% | 96.6% | 101.5% | 101.1% | 98.7% | 98.9% | 100.4% | 100.8% | 101.7% | 102.4% | 99.5% | 102.6% | 101.1% | 96.1% | 101.6% | 100.5% | 99.2% | 98.4% | 100.8% | 99.8% | 100.0% | 102.3% | 100.6% | 100.9% | 101.9% | 102.7% | 97.7% | 102.3% | 103.6% | 99.5% | 100.3% | 101.5% | 101.6% | 101.7% | 106.3% | 97.3% | 102.3% | 102.1% | 100.6% | 100.5% | 99.7% | 102.8% |
| 2010-07-01 | 99.9% | 101.5% | 102.6% | 101.8% | 100.3% | 101.9% | 99.5% | 102.6% | 97.6% | 105.3% | 100.1% | 96.6% | 101.8% | 101.0% | 98.5% | 98.9% | 100.2% | 100.7% | 101.7% | 102.4% | 99.4% | 102.7% | 101.1% | 96.0% | 101.6% | 101.8% | 99.2% | 98.3% | 100.8% | 99.7% | 100.0% | 102.1% | 100.5% | 100.7% | 101.8% | 102.8% | 97.5% | 102.3% | 103.6% | 99.5% | 100.3% | 101.6% | 101.6% | 101.8% | 106.4% | 97.2% | 102.2% | 102.1% | 100.5% | 100.4% | 99.6% | 102.7% |
| 2010-08-01 | 100.1% | 101.5% | 102.6% | 101.5% | 100.3% | 101.9% | 99.5% | 102.7% | 97.8% | 105.2% | 100.3% | 96.6% | 102.1% | 100.9% | 98.4% | 98.8% | 100.1% | 100.7% | 101.8% | 102.4% | 99.4% | 102.8% | 101.1% | 95.6% | 101.6% | 102.6% | 99.2% | 98.3% | 100.9% | 99.6% | 99.9% | 102.1% | 100.3% | 100.6% | 101.6% | 102.9% | 97.3% | 102.3% | 103.7% | 99.5% | 100.2% | 101.7% | 101.7% | 101.8% | 106.6% | 97.0% | 102.1% | 102.1% | 100.5% | 100.4% | 99.5% | 102.7% |
| 2010-09-01 | 100.0% | 101.5% | 102.7% | 101.3% | 100.3% | 101.9% | 99.5% | 102.7% | 97.9% | 105.2% | 100.5% | 96.7% | 102.3% | 100.8% | 98.4% | 98.6% | 100.1% | 100.7% | 101.9% | 102.3% | 99.5% | 102.8% | 101.1% | 95.3% | 101.6% | 103.0% | 99.3% | 98.2% | 100.9% | 99.6% | 99.9% | 102.0% | 100.1% | 100.4% | 101.6% | 103.1% | 97.2% | 102.3% | 103.7% | 99.5% | 100.1% | 101.8% | 101.7% | 101.8% | 106.7% | 96.9% | 102.1% | 102.2% | 100.4% | 100.4% | 99.5% | 102.7% |
| 2010-10-01 | 99.8% | 101.6% | 102.9% | 101.2% | 100.2% | 101.9% | 99.6% | 102.8% | 98.0% | 105.2% | 100.6% | 96.9% | 102.6% | 100.8% | 98.3% | 98.5% | 100.2% | 100.7% | 102.0% | 102.3% | 99.6% | 102.9% | 101.2% | 94.9% | 101.6% | 103.2% | 99.3% | 98.1% | 101.0% | 99.7% | 99.8% | 102.0% | 100.0% | 100.3% | 101.7% | 103.3% | 97.1% | 102.2% | 103.8% | 99.6% | 99.9% | 101.9% | 101.7% | 101.9% | 106.9% | 96.9% | 102.1% | 102.2% | 100.4% | 100.3% | 99.5% | 102.8% |
| 2010-11-01 | 100.1% | 101.6% | 103.0% | 101.0% | 100.2% | 101.9% | 99.6% | 102.8% | 98.1% | 105.5% | 100.9% | 96.9% | 102.9% | 100.8% | 98.2% | 98.5% | 100.3% | 100.8% | 102.0% | 102.2% | 99.7% | 103.0% | 101.2% | 94.6% | 101.6% | 103.3% | 99.3% | 98.1% | 101.1% | 99.7% | 99.7% | 102.0% | 99.9% | 100.1% | 101.8% | 103.5% | 97.0% | 102.2% | 103.9% | 99.6% | 99.8% | 101.9% | 101.8% | 102.0% | 107.1% | 96.8% | 102.1% | 102.3% | 100.4% | 100.3% | 99.5% | 102.9% |
| 2010-12-01 | 99.8% | 101.5% | 103.1% | 100.9% | 100.2% | 101.9% | 99.6% | 102.7% | 98.2% | 105.7% | 100.9% | 97.0% | 103.1% | 100.8% | 98.0% | 98.4% | 100.4% | 100.8% | 102.0% | 102.2% | 99.7% | 103.0% | 101.2% | 94.2% | 101.6% | 103.3% | 99.3% | 98.0% | 101.2% | 99.7% | 99.6% | 102.0% | 99.8% | 100.0% | 101.9% | 103.7% | 96.8% | 102.2% | 103.9% | 99.6% | 99.5% | 101.9% | 101.9% | 102.1% | 107.3% | 96.8% | 102.1% | 102.4% | 100.3% | 100.2% | 99.4% | 103.0% |
| 2011-01-01 | 99.6% | 101.4% | 103.2% | 100.7% | 100.2% | 101.8% | 99.6% | 102.6% | 98.4% | 106.0% | 101.0% | 97.0% | 103.4% | 100.8% | 97.9% | 98.5% | 100.4% | 100.8% | 101.9% | 102.1% | 99.7% | 103.0% | 101.2% | 93.9% | 101.7% | 103.4% | 99.2% | 98.0% | 101.4% | 99.7% | 99.5% | 102.0% | 99.8% | 99.9% | 102.0% | 103.9% | 96.7% | 102.1% | 103.9% | 99.6% | 99.3% | 101.9% | 102.0% | 102.2% | 107.5% | 96.8% | 102.1% | 102.5% | 100.2% | 100.1% | 99.4% | 103.0% |
| 2011-02-01 | 99.5% | 101.4% | 103.2% | 100.6% | 100.2% | 101.8% | 99.7% | 102.6% | 98.5% | 106.1% | 101.0% | 97.1% | 103.5% | 100.9% | 97.7% | 98.5% | 100.4% | 100.8% | 101.9% | 102.0% | 99.7% | 103.0% | 101.2% | 93.8% | 101.7% | 103.4% | 99.2% | 98.0% | 101.5% | 99.7% | 99.5% | 102.0% | 99.7% | 99.8% | 102.0% | 104.1% | 96.5% | 102.1% | 103.8% | 99.6% | 99.1% | 101.8% | 102.0% | 102.4% | 107.6% | 96.8% | 102.1% | 102.6% | 100.1% | 99.9% | 99.3% | 103.0% |
| 2011-03-01 | 99.6% | 101.3% | 103.2% | 100.5% | 100.1% | 101.8% | 99.7% | 102.5% | 98.7% | 106.2% | 101.0% | 97.1% | 103.6% | 100.9% | 97.7% | 98.6% | 100.2% | 100.7% | 101.8% | 101.9% | 99.6% | 103.0% | 101.1% | 93.4% | 101.8% | 103.4% | 99.1% | 98.0% | 101.6% | 99.7% | 99.4% | 102.0% | 99.6% | 99.7% | 102.0% | 104.2% | 96.3% | 102.0% | 103.8% | 99.6% | 98.9% | 101.8% | 101.9% | 102.4% | 107.8% | 96.8% | 102.0% | 102.7% | 100.0% | 99.8% | 99.3% | 102.9% |
| 2011-04-01 | 99.8% | 101.2% | 103.2% | 100.4% | 100.0% | 101.8% | 99.7% | 102.4% | 98.7% | 106.2% | 101.0% | 97.2% | 103.6% | 100.9% | 97.6% | 98.7% | 100.1% | 100.6% | 101.7% | 101.7% | 99.5% | 102.9% | 101.0% | 93.5% | 101.8% | 103.4% | 99.0% | 98.0% | 101.7% | 99.7% | 99.4% | 102.0% | 99.6% | 99.5% | 102.1% | 104.2% | 96.1% | 101.9% | 103.7% | 99.6% | 98.7% | 101.9% | 101.9% | 102.5% | 107.9% | 96.8% | 101.8% | 102.7% | 99.9% | 99.6% | 99.2% | 102.8% |
| 2011-05-01 | 99.7% | 101.0% | 103.2% | 100.3% | 99.9% | 101.8% | 99.7% | 102.3% | 98.8% | 106.3% | 100.9% | 97.3% | 103.5% | 101.0% | 97.7% | 98.9% | 100.0% | 100.5% | 101.6% | 101.5% | 99.5% | 102.9% | 101.0% | 93.6% | 101.9% | 103.4% | 98.9% | 97.9% | 101.7% | 99.7% | 99.3% | 102.0% | 99.6% | 99.4% | 102.1% | 104.3% | 96.0% | 101.9% | 103.6% | 99.6% | 98.5% | 101.9% | 101.8% | 102.4% | 108.1% | 96.8% | 101.6% | 102.8% | 99.9% | 99.5% | 99.2% | 102.7% |
| 2011-06-01 | 99.6% | 100.9% | 103.3% | 100.3% | 99.9% | 101.9% | 99.9% | 102.3% | 98.8% | 106.3% | 101.0% | 97.4% | 103.5% | 101.0% | 97.8% | 99.0% | 99.9% | 100.5% | 101.6% | 101.5% | 99.5% | 102.9% | 101.0% | 93.8% | 102.0% | 103.4% | 98.9% | 98.0% | 101.8% | 99.8% | 99.3% | 102.1% | 99.6% | 99.4% | 102.2% | 104.5% | 96.0% | 102.0% | 103.6% | 99.6% | 98.3% | 102.0% | 101.7% | 102.3% | 108.4% | 96.9% | 101.5% | 102.8% | 99.8% | 99.5% | 99.2% | 102.8% |
| 2011-07-01 | 99.6% | 100.8% | 103.4% | 100.2% | 100.1% | 102.0% | 100.1% | 102.3% | 98.9% | 106.5% | 101.0% | 97.6% | 103.4% | 101.1% | 98.0% | 99.2% | 99.8% | 100.5% | 101.5% | 101.5% | 99.6% | 103.0% | 101.1% | 93.9% | 102.0% | 103.4% | 98.9% | 98.1% | 101.9% | 99.9% | 99.4% | 102.2% | 99.7% | 99.4% | 102.3% | 104.7% | 95.9% | 102.2% | 103.6% | 99.8% | 98.2% | 102.1% | 101.8% | 102.3% | 108.7% | 96.6% | 101.4% | 103.0% | 99.8% | 99.7% | 99.2% | 102.9% |
| 2011-08-01 | 99.9% | 100.7% | 103.7% | 100.2% | 100.3% | 102.2% | 100.3% | 102.4% | 99.0% | 106.6% | 101.1% | 97.8% | 103.4% | 101.3% | 98.1% | 99.4% | 99.8% | 100.6% | 101.5% | 101.6% | 99.7% | 103.1% | 101.2% | 94.0% | 102.1% | 103.3% | 98.9% | 98.3% | 102.1% | 100.1% | 99.5% | 102.3% | 99.8% | 99.5% | 102.5% | 105.0% | 95.9% | 102.4% | 103.7% | 99.9% | 98.2% | 102.1% | 101.9% | 102.2% | 108.8% | 96.4% | 101.4% | 103.2% | 99.8% | 99.8% | 99.3% | 103.1% |
| 2011-09-01 | 100.1% | 100.6% | 103.8% | 100.2% | 100.6% | 102.3% | 100.6% | 102.5% | 99.2% | 106.8% | 101.2% | 98.0% | 103.3% | 101.5% | 98.2% | 99.5% | 99.9% | 100.6% | 101.5% | 101.8% | 99.8% | 103.2% | 101.4% | 94.2% | 102.1% | 103.3% | 98.9% | 98.6% | 102.2% | 100.2% | 99.7% | 102.4% | 99.9% | 99.7% | 102.6% | 105.3% | 95.7% | 102.7% | 103.7% | 100.1% | 98.1% | 102.2% | 102.0% | 102.1% | 108.9% | 96.3% | 101.4% | 103.4% | 99.8% | 100.0% | 99.4% | 103.4% |
| 2011-10-01 | 100.0% | 100.5% | 103.9% | 100.2% | 100.7% | 102.4% | 100.8% | 102.6% | 99.3% | 107.0% | 101.3% | 98.1% | 103.2% | 101.7% | 98.3% | 99.6% | 99.9% | 100.7% | 101.5% | 102.0% | 99.9% | 103.3% | 101.5% | 94.2% | 102.0% | 103.2% | 98.8% | 98.8% | 102.4% | 100.2% | 99.8% | 102.5% | 100.0% | 99.8% | 102.7% | 105.6% | 95.6% | 103.0% | 103.7% | 100.2% | 98.1% | 102.2% | 102.2% | 102.0% | 109.0% | 96.2% | 101.3% | 103.5% | 99.9% | 100.2% | 99.5% | 103.6% |
| 2011-11-01 | 100.1% | 100.3% | 103.9% | 100.2% | 100.8% | 102.5% | 100.9% | 102.6% | 99.4% | 107.2% | 101.4% | 98.2% | 103.0% | 101.8% | 98.3% | 99.6% | 99.9% | 100.6% | 101.4% | 102.1% | 99.9% | 103.4% | 101.6% | 94.3% | 102.0% | 103.1% | 98.7% | 98.9% | 102.5% | 100.3% | 99.8% | 102.5% | 100.0% | 99.9% | 102.8% | 105.9% | 95.5% | 103.3% | 103.6% | 100.3% | 98.1% | 102.2% | 102.2% | 101.9% | 109.1% | 96.1% | 101.3% | 103.6% | 100.0% | 100.2% | 99.5% | 103.7% |
| 2011-12-01 | 100.1% | 100.1% | 103.8% | 100.2% | 100.8% | 102.4% | 100.9% | 102.5% | 99.5% | 107.4% | 101.4% | 98.2% | 102.7% | 102.0% | 98.2% | 99.5% | 99.8% | 100.5% | 101.3% | 102.1% | 99.9% | 103.5% | 101.7% | 94.2% | 101.9% | 102.9% | 98.5% | 98.9% | 102.5% | 100.2% | 99.8% | 102.5% | 100.0% | 99.9% | 102.9% | 106.1% | 95.4% | 103.4% | 103.5% | 100.3% | 98.0% | 102.1% | 102.2% | 101.7% | 109.1% | 96.0% | 101.1% | 103.6% | 100.1% | 100.2% | 99.4% | 103.7% |
| 2012-01-01 | 100.3% | 99.8% | 103.7% | 100.2% | 100.7% | 102.4% | 100.8% | 102.4% | 99.5% | 107.7% | 101.5% | 98.1% | 102.4% | 102.1% | 98.1% | 99.3% | 99.7% | 100.4% | 101.1% | 102.2% | 99.8% | 103.5% | 101.7% | 94.2% | 101.8% | 102.7% | 98.3% | 98.9% | 102.5% | 100.1% | 99.8% | 102.5% | 100.0% | 100.0% | 103.0% | 106.2% | 95.3% | 103.5% | 103.3% | 100.3% | 97.8% | 102.1% | 102.2% | 101.6% | 109.0% | 96.1% | 100.9% | 103.5% | 100.3% | 100.1% | 99.3% | 103.7% |
| 2012-02-01 | 100.5% | 99.7% | 103.6% | 100.2% | 100.5% | 102.3% | 100.7% | 102.2% | 99.5% | 108.1% | 101.5% | 98.1% | 102.2% | 102.1% | 98.1% | 99.1% | 99.6% | 100.3% | 101.0% | 102.2% | 99.8% | 103.5% | 101.7% | 94.1% | 101.7% | 102.4% | 98.1% | 98.9% | 102.5% | 100.1% | 99.7% | 102.4% | 100.0% | 100.0% | 103.0% | 106.3% | 95.3% | 103.6% | 103.1% | 100.4% | 97.7% | 102.0% | 102.1% | 101.5% | 109.1% | 95.8% | 100.8% | 103.4% | 100.5% | 100.1% | 99.2% | 103.6% |
| 2012-03-01 | 100.5% | 99.6% | 103.5% | 100.3% | 100.3% | 102.3% | 100.6% | 101.9% | 99.5% | 108.5% | 101.6% | 98.1% | 102.0% | 102.2% | 98.0% | 98.8% | 99.5% | 100.1% | 101.0% | 102.3% | 99.8% | 103.5% | 101.7% | 94.0% | 101.6% | 102.3% | 98.0% | 99.0% | 102.5% | 100.2% | 99.8% | 102.4% | 99.9% | 100.1% | 103.1% | 106.5% | 95.2% | 103.7% | 102.9% | 100.5% | 97.7% | 102.1% | 102.1% | 101.4% | 109.0% | 96.1% | 100.7% | 103.3% | 100.8% | 100.1% | 99.2% | 103.5% |
| 2012-04-01 | 100.4% | 99.6% | 103.4% | 100.3% | 100.2% | 102.3% | 100.6% | 101.7% | 99.5% | 109.1% | 101.7% | 98.1% | 101.8% | 102.2% | 98.0% | 98.6% | 99.4% | 100.1% | 101.0% | 102.4% | 99.8% | 103.6% | 101.8% | 94.0% | 101.6% | 102.1% | 97.9% | 99.1% | 102.5% | 100.2% | 99.8% | 102.5% | 99.9% | 100.1% | 103.2% | 106.6% | 95.1% | 103.8% | 102.6% | 100.6% | 97.7% | 102.1% | 102.1% | 101.4% | 109.2% | 96.4% | 100.6% | 103.2% | 100.9% | 100.1% | 99.2% | 103.5% |
| 2012-05-01 | 100.6% | 99.6% | 103.4% | 100.4% | 100.0% | 102.4% | 100.7% | 101.4% | 99.5% | 109.6% | 101.8% | 98.2% | 101.7% | 102.2% | 98.1% | 98.4% | 99.3% | 100.0% | 101.2% | 102.4% | 99.9% | 103.6% | 101.8% | 94.0% | 101.6% | 102.1% | 97.9% | 99.2% | 102.6% | 100.3% | 99.9% | 102.5% | 99.9% | 100.2% | 103.3% | 106.8% | 95.0% | 103.9% | 102.4% | 100.8% | 97.8% | 102.1% | 102.1% | 101.4% | 109.4% | 96.6% | 100.6% | 103.1% | 101.0% | 100.2% | 99.2% | 103.4% |
| 2012-06-01 | 100.8% | 99.7% | 103.4% | 100.4% | 99.8% | 102.4% | 100.7% | 101.1% | 99.5% | 110.2% | 101.9% | 98.2% | 101.7% | 102.3% | 98.1% | 98.3% | 99.2% | 100.0% | 101.4% | 102.3% | 99.9% | 103.8% | 101.9% | 94.1% | 101.6% | 102.0% | 97.9% | 99.4% | 102.7% | 100.4% | 100.0% | 102.5% | 99.9% | 100.3% | 103.5% | 107.0% | 94.9% | 104.0% | 102.2% | 100.9% | 98.0% | 102.1% | 102.2% | 101.4% | 109.5% | 96.9% | 100.5% | 103.1% | 101.1% | 100.2% | 99.2% | 103.4% |
| 2012-07-01 | 100.7% | 99.8% | 103.3% | 100.5% | 99.6% | 102.5% | 100.8% | 100.8% | 99.5% | 110.7% | 102.0% | 98.3% | 101.6% | 102.3% | 98.2% | 98.3% | 99.2% | 100.0% | 101.6% | 102.3% | 99.9% | 103.9% | 102.0% | 94.2% | 101.7% | 102.0% | 97.9% | 99.5% | 102.9% | 100.4% | 100.1% | 102.5% | 100.0% | 100.4% | 103.7% | 107.2% | 94.8% | 104.1% | 101.9% | 101.1% | 98.2% | 102.2% | 102.3% | 101.4% | 109.7% | 97.1% | 100.5% | 103.2% | 101.0% | 100.2% | 99.2% | 103.5% |
| 2012-08-01 | 100.5% | 99.9% | 103.3% | 100.5% | 99.5% | 102.6% | 100.9% | 100.6% | 99.4% | 111.4% | 102.1% | 98.3% | 101.6% | 102.4% | 98.3% | 98.3% | 99.2% | 100.1% | 101.8% | 102.2% | 100.0% | 104.1% | 102.0% | 94.3% | 101.9% | 102.0% | 97.9% | 99.6% | 103.1% | 100.5% | 100.3% | 102.6% | 100.2% | 100.5% | 104.0% | 107.3% | 94.8% | 104.2% | 101.7% | 101.2% | 98.4% | 102.2% | 102.4% | 101.5% | 109.8% | 97.4% | 100.5% | 103.3% | 100.9% | 100.2% | 99.2% | 103.5% |
| 2012-09-01 | 100.8% | 100.0% | 103.4% | 100.6% | 99.3% | 102.7% | 101.0% | 100.4% | 99.4% | 112.0% | 102.2% | 98.4% | 101.6% | 102.4% | 98.3% | 98.4% | 99.3% | 100.2% | 102.0% | 102.2% | 100.1% | 104.2% | 102.1% | 94.4% | 102.0% | 102.0% | 98.0% | 99.7% | 103.3% | 100.5% | 100.4% | 102.6% | 100.4% | 100.6% | 104.2% | 107.4% | 94.8% | 104.4% | 101.6% | 101.3% | 98.6% | 102.4% | 102.4% | 101.6% | 110.0% | 97.7% | 100.5% | 103.4% | 100.8% | 100.2% | 99.3% | 103.5% |
| 2012-10-01 | 101.1% | 100.0% | 103.5% | 100.6% | 99.2% | 102.8% | 101.2% | 100.3% | 99.4% | 112.5% | 102.3% | 98.4% | 101.6% | 102.5% | 98.4% | 98.5% | 99.4% | 100.2% | 102.2% | 102.3% | 100.1% | 104.4% | 102.2% | 94.5% | 102.2% | 102.0% | 98.1% | 99.8% | 103.4% | 100.5% | 100.5% | 102.7% | 100.6% | 100.7% | 104.4% | 107.6% | 94.8% | 104.5% | 101.3% | 101.4% | 98.7% | 102.5% | 102.5% | 101.7% | 110.1% | 98.0% | 100.4% | 103.6% | 100.8% | 100.1% | 99.4% | 103.4% |
| 2012-11-01 | 100.9% | 100.1% | 103.5% | 100.6% | 99.1% | 102.9% | 101.3% | 100.2% | 99.4% | 112.9% | 102.4% | 98.4% | 101.6% | 102.5% | 98.4% | 98.6% | 99.5% | 100.3% | 102.2% | 102.5% | 100.2% | 104.5% | 102.2% | 94.7% | 102.3% | 101.9% | 98.2% | 99.8% | 103.5% | 100.6% | 100.6% | 102.7% | 100.6% | 100.8% | 104.6% | 107.7% | 94.8% | 104.5% | 101.1% | 101.3% | 98.7% | 102.6% | 102.5% | 101.8% | 110.3% | 98.2% | 100.3% | 103.7% | 100.7% | 100.1% | 99.4% | 103.3% |
| 2012-12-01 | 101.1% | 100.0% | 103.5% | 100.6% | 99.0% | 102.9% | 101.3% | 100.1% | 99.3% | 113.2% | 102.4% | 98.3% | 101.5% | 102.5% | 98.3% | 98.7% | 99.6% | 100.3% | 102.2% | 102.6% | 100.3% | 104.5% | 102.2% | 94.8% | 102.3% | 101.8% | 98.2% | 99.9% | 103.5% | 100.6% | 100.6% | 102.7% | 100.6% | 100.8% | 104.6% | 107.8% | 94.8% | 104.5% | 100.8% | 101.2% | 98.6% | 102.7% | 102.4% | 101.8% | 110.4% | 98.4% | 100.1% | 103.7% | 100.5% | 99.9% | 99.5% | 103.2% |
| 2013-01-01 | 101.2% | 99.9% | 103.4% | 100.6% | 98.9% | 102.9% | 101.3% | 99.9% | 99.1% | 113.4% | 102.4% | 98.2% | 101.4% | 102.4% | 98.2% | 98.7% | 99.6% | 100.2% | 102.1% | 102.7% | 100.3% | 104.5% | 102.1% | 94.9% | 102.4% | 101.0% | 98.2% | 99.9% | 103.4% | 100.5% | 100.5% | 102.5% | 100.5% | 100.8% | 104.6% | 107.9% | 94.7% | 104.4% | 100.5% | 101.1% | 98.5% | 102.7% | 102.4% | 101.7% | 110.5% | 98.6% | 100.0% | 103.7% | 100.5% | 99.7% | 99.5% | 103.1% |
| 2013-02-01 | 100.9% | 99.8% | 103.3% | 100.5% | 98.8% | 102.9% | 101.3% | 99.8% | 99.0% | 113.4% | 102.4% | 98.1% | 101.3% | 102.4% | 98.0% | 98.7% | 99.6% | 100.2% | 102.0% | 102.8% | 100.3% | 104.4% | 102.1% | 94.9% | 102.3% | 100.3% | 98.1% | 100.0% | 103.4% | 100.5% | 100.4% | 102.4% | 100.4% | 100.7% | 104.2% | 108.1% | 94.7% | 104.3% | 100.3% | 100.9% | 98.3% | 102.7% | 102.3% | 101.6% | 110.6% | 98.7% | 99.8% | 103.6% | 100.2% | 99.4% | 99.5% | 102.9% |
| 2013-03-01 | 100.7% | 99.7% | 103.2% | 100.5% | 98.7% | 102.9% | 101.3% | 99.7% | 98.8% | 113.4% | 102.5% | 98.0% | 101.3% | 102.5% | 97.9% | 98.8% | 99.6% | 100.1% | 101.8% | 102.9% | 100.4% | 104.4% | 102.1% | 95.0% | 102.3% | 99.5% | 98.2% | 100.1% | 103.3% | 100.5% | 100.4% | 102.2% | 100.3% | 100.7% | 103.9% | 108.3% | 94.8% | 104.3% | 100.1% | 100.8% | 98.1% | 102.6% | 102.3% | 101.5% | 110.8% | 98.9% | 99.7% | 103.6% | 100.2% | 99.2% | 99.5% | 102.9% |
| 2013-04-01 | 101.0% | 99.6% | 103.2% | 100.5% | 98.6% | 103.0% | 101.4% | 99.8% | 98.7% | 113.4% | 102.6% | 98.0% | 101.4% | 102.6% | 97.9% | 98.9% | 99.9% | 100.1% | 101.7% | 102.9% | 100.4% | 104.4% | 102.2% | 95.2% | 102.2% | 98.9% | 98.2% | 100.2% | 103.4% | 100.6% | 100.4% | 102.0% | 100.3% | 100.7% | 103.7% | 108.5% | 94.9% | 104.3% | 100.0% | 100.7% | 98.0% | 102.6% | 102.4% | 101.4% | 110.9% | 99.2% | 99.6% | 103.7% | 100.3% | 99.1% | 99.6% | 102.9% |
| 2013-05-01 | 101.1% | 99.6% | 103.2% | 100.6% | 98.6% | 103.0% | 101.5% | 99.9% | 98.7% | 113.4% | 102.7% | 98.0% | 101.5% | 102.8% | 97.9% | 99.0% | 100.2% | 100.2% | 101.7% | 103.0% | 100.5% | 104.3% | 102.3% | 95.3% | 102.2% | 98.2% | 98.3% | 100.2% | 103.4% | 100.7% | 100.4% | 101.8% | 100.2% | 100.8% | 103.5% | 108.7% | 95.0% | 104.4% | 99.9% | 100.6% | 97.9% | 102.7% | 102.4% | 101.3% | 111.1% | 99.5% | 99.6% | 103.8% | 100.4% | 99.1% | 99.7% | 102.9% |
| 2013-06-01 | 101.2% | 99.6% | 103.3% | 100.7% | 98.5% | 103.1% | 101.5% | 100.0% | 98.7% | 113.3% | 102.8% | 98.0% | 101.7% | 103.0% | 97.9% | 99.2% | 100.6% | 100.2% | 101.7% | 103.0% | 100.6% | 104.3% | 102.3% | 95.5% | 102.2% | 97.6% | 98.4% | 100.3% | 103.3% | 100.8% | 100.5% | 101.7% | 100.3% | 100.9% | 103.3% | 108.8% | 95.0% | 104.5% | 99.9% | 100.6% | 97.9% | 102.7% | 102.4% | 101.2% | 111.3% | 99.8% | 99.5% | 103.9% | 100.6% | 99.1% | 99.7% | 102.9% |
| 2013-07-01 | 101.1% | 99.6% | 103.3% | 100.8% | 98.4% | 103.1% | 101.6% | 100.2% | 98.7% | 113.2% | 102.9% | 97.9% | 101.9% | 103.2% | 97.9% | 99.3% | 100.8% | 100.2% | 101.6% | 103.0% | 100.7% | 104.3% | 102.4% | 95.6% | 102.2% | 97.3% | 98.4% | 100.3% | 103.2% | 100.8% | 100.5% | 101.5% | 100.2% | 101.0% | 103.1% | 108.9% | 95.0% | 104.5% | 99.9% | 100.5% | 97.9% | 102.7% | 102.4% | 101.0% | 111.5% | 100.0% | 99.5% | 104.0% | 100.7% | 99.0% | 99.7% | 102.9% |
| 2013-08-01 | 101.1% | 99.5% | 103.3% | 100.9% | 98.3% | 103.1% | 101.6% | 100.2% | 98.8% | 113.1% | 103.0% | 97.8% | 102.0% | 103.4% | 97.8% | 99.5% | 101.0% | 100.1% | 101.4% | 103.0% | 100.7% | 104.2% | 102.3% | 95.6% | 102.2% | 96.3% | 98.3% | 100.4% | 103.1% | 100.8% | 100.5% | 101.2% | 100.2% | 100.9% | 103.0% | 108.9% | 95.0% | 104.4% | 99.9% | 100.4% | 97.9% | 102.7% | 102.4% | 100.8% | 111.6% | 100.2% | 99.4% | 104.0% | 100.7% | 99.0% | 99.6% | 102.9% |
| 2013-09-01 | 101.1% | 99.4% | 103.3% | 100.9% | 98.2% | 103.0% | 101.5% | 100.2% | 98.9% | 113.0% | 103.0% | 97.6% | 102.2% | 103.6% | 97.6% | 99.6% | 101.0% | 100.0% | 101.1% | 102.9% | 100.6% | 104.0% | 102.2% | 95.5% | 102.2% | 96.1% | 98.2% | 100.4% | 102.9% | 100.7% | 100.4% | 100.9% | 100.2% | 100.8% | 102.6% | 108.9% | 94.9% | 104.3% | 99.8% | 100.2% | 97.8% | 102.6% | 102.3% | 100.6% | 111.6% | 100.4% | 99.3% | 104.0% | 100.8% | 98.8% | 99.5% | 102.9% |
| 2013-10-01 | 100.5% | 99.3% | 103.2% | 100.9% | 98.0% | 102.9% | 101.5% | 100.1% | 99.0% | 113.0% | 103.0% | 97.5% | 102.4% | 103.7% | 97.5% | 99.6% | 100.9% | 99.9% | 100.8% | 102.8% | 100.5% | 103.9% | 102.2% | 95.4% | 102.2% | 96.0% | 98.2% | 100.5% | 102.8% | 100.7% | 100.4% | 100.6% | 100.2% | 100.5% | 102.6% | 108.9% | 94.8% | 104.2% | 99.9% | 100.1% | 97.7% | 102.5% | 102.3% | 100.3% | 111.7% | 100.5% | 99.2% | 104.0% | 100.8% | 98.7% | 99.4% | 102.9% |
| 2013-11-01 | 100.9% | 99.2% | 103.2% | 101.0% | 97.9% | 102.9% | 101.5% | 100.1% | 99.2% | 113.1% | 103.1% | 97.4% | 102.7% | 103.5% | 97.5% | 99.6% | 100.9% | 99.9% | 100.5% | 102.8% | 100.3% | 103.8% | 102.2% | 95.4% | 102.3% | 95.8% | 98.3% | 100.5% | 102.8% | 100.7% | 100.3% | 100.4% | 100.2% | 100.3% | 102.6% | 109.0% | 94.7% | 104.1% | 100.0% | 100.0% | 97.6% | 102.4% | 102.4% | 100.2% | 111.8% | 100.6% | 99.2% | 104.1% | 100.8% | 98.7% | 99.3% | 102.9% |
| 2013-12-01 | 100.8% | 99.2% | 103.3% | 101.1% | 97.9% | 102.9% | 101.7% | 100.2% | 99.4% | 113.2% | 103.3% | 97.5% | 102.9% | 103.3% | 97.5% | 99.7% | 100.9% | 100.0% | 100.3% | 102.9% | 100.2% | 103.8% | 102.4% | 95.5% | 102.3% | 95.7% | 98.5% | 100.5% | 102.8% | 100.8% | 100.2% | 100.3% | 100.2% | 100.2% | 102.6% | 109.0% | 94.7% | 104.1% | 100.2% | 99.9% | 97.6% | 102.4% | 102.5% | 100.0% | 111.9% | 100.8% | 99.1% | 104.2% | 100.8% | 98.7% | 99.3% | 102.9% |
| 2014-01-01 | 100.9% | 99.2% | 103.4% | 101.3% | 97.9% | 103.0% | 101.9% | 100.3% | 99.6% | 113.3% | 103.5% | 97.6% | 103.2% | 103.1% | 97.5% | 99.8% | 101.0% | 100.1% | 100.1% | 103.0% | 100.1% | 103.8% | 102.6% | 95.5% | 102.4% | 95.7% | 98.6% | 100.5% | 102.9% | 100.9% | 100.2% | 100.3% | 100.2% | 100.0% | 102.7% | 109.2% | 94.6% | 104.0% | 100.4% | 100.0% | 97.5% | 102.5% | 102.6% | 99.9% | 112.1% | 101.0% | 99.1% | 104.3% | 100.9% | 98.8% | 99.3% | 103.0% |
| 2014-02-01 | 101.0% | 99.3% | 103.5% | 101.5% | 97.8% | 103.1% | 102.2% | 100.5% | 99.8% | 113.4% | 103.7% | 97.7% | 103.4% | 102.9% | 97.5% | 99.9% | 101.2% | 100.2% | 100.0% | 103.1% | 100.0% | 103.8% | 102.8% | 95.6% | 102.4% | 95.7% | 98.8% | 100.5% | 103.0% | 101.0% | 100.2% | 100.3% | 100.2% | 99.9% | 102.8% | 109.4% | 94.6% | 103.9% | 100.6% | 100.0% | 97.5% | 102.6% | 102.7% | 99.8% | 112.3% | 101.1% | 99.0% | 104.4% | 100.9% | 98.8% | 99.3% | 103.0% |
| 2014-03-01 | 101.4% | 99.3% | 103.6% | 101.7% | 97.8% | 103.2% | 102.4% | 100.6% | 100.1% | 113.6% | 103.9% | 97.7% | 103.5% | 102.8% | 97.5% | 100.0% | 101.4% | 100.4% | 99.8% | 103.4% | 99.9% | 103.8% | 103.0% | 95.7% | 102.5% | 95.6% | 98.9% | 100.4% | 103.1% | 101.0% | 100.3% | 100.3% | 100.2% | 99.7% | 102.9% | 109.7% | 94.6% | 103.8% | 100.8% | 100.0% | 97.5% | 102.7% | 102.8% | 99.7% | 112.4% | 101.2% | 99.0% | 104.5% | 100.9% | 98.8% | 99.3% | 103.0% |
| 2014-04-01 | 100.9% | 99.3% | 103.6% | 101.9% | 97.8% | 103.3% | 102.6% | 100.8% | 100.3% | 113.9% | 104.0% | 97.8% | 103.7% | 102.6% | 97.4% | 100.2% | 101.5% | 100.4% | 99.6% | 103.7% | 99.8% | 103.9% | 103.2% | 95.8% | 102.6% | 95.5% | 98.9% | 100.4% | 103.0% | 101.1% | 100.3% | 100.4% | 100.3% | 99.6% | 103.0% | 110.0% | 94.6% | 103.8% | 101.0% | 100.0% | 97.5% | 102.9% | 102.9% | 99.6% | 112.5% | 101.3% | 99.0% | 104.6% | 101.0% | 98.7% | 99.3% | 103.0% |
| 2014-05-01 | 101.1% | 99.2% | 103.7% | 102.1% | 97.8% | 103.4% | 102.7% | 100.9% | 100.6% | 114.2% | 104.1% | 97.8% | 103.8% | 102.7% | 97.2% | 100.3% | 101.7% | 100.4% | 99.3% | 104.1% | 99.7% | 103.9% | 103.4% | 95.8% | 102.7% | 95.4% | 98.9% | 100.5% | 102.9% | 101.1% | 100.3% | 100.5% | 100.3% | 99.5% | 103.1% | 110.3% | 94.7% | 103.8% | 101.1% | 99.9% | 97.5% | 103.2% | 102.9% | 99.6% | 112.7% | 101.5% | 99.0% | 104.6% | 101.1% | 98.6% | 99.4% | 103.1% |
| 2014-06-01 | 101.2% | 99.1% | 103.6% | 102.3% | 97.9% | 103.5% | 102.7% | 101.1% | 100.9% | 114.6% | 104.2% | 97.8% | 103.9% | 102.4% | 97.1% | 100.3% | 101.8% | 100.4% | 99.0% | 104.6% | 99.6% | 104.0% | 103.6% | 95.8% | 102.8% | 95.4% | 98.9% | 100.6% | 102.8% | 101.2% | 100.3% | 100.6% | 100.4% | 99.4% | 103.2% | 110.7% | 94.8% | 103.8% | 101.3% | 99.9% | 97.5% | 103.5% | 103.0% | 99.6% | 112.8% | 101.6% | 99.0% | 104.5% | 101.3% | 98.5% | 99.4% | 103.2% |
| 2014-07-01 | 101.4% | 99.1% | 103.6% | 102.5% | 98.0% | 103.6% | 102.8% | 101.3% | 101.1% | 115.1% | 104.3% | 97.8% | 104.0% | 102.6% | 97.0% | 100.4% | 101.9% | 100.4% | 98.7% | 105.1% | 99.5% | 104.0% | 103.8% | 95.8% | 103.0% | 95.3% | 98.9% | 100.6% | 102.8% | 101.3% | 100.4% | 100.7% | 100.5% | 99.4% | 103.3% | 111.0% | 95.0% | 104.0% | 101.4% | 99.8% | 97.5% | 103.8% | 103.1% | 99.6% | 112.9% | 101.9% | 99.1% | 104.4% | 101.5% | 98.4% | 99.5% | 103.2% |
| 2014-08-01 | 101.4% | 99.1% | 103.5% | 102.8% | 98.1% | 103.7% | 102.9% | 101.4% | 101.4% | 115.6% | 104.4% | 97.8% | 104.1% | 102.8% | 97.0% | 100.5% | 102.0% | 100.4% | 98.5% | 105.6% | 99.4% | 104.1% | 104.1% | 95.8% | 103.1% | 95.3% | 99.0% | 100.7% | 102.8% | 101.4% | 100.5% | 100.9% | 100.6% | 99.3% | 103.4% | 111.4% | 95.2% | 104.2% | 101.6% | 99.9% | 97.5% | 104.2% | 103.2% | 99.7% | 113.1% | 102.1% | 99.1% | 104.3% | 101.8% | 98.4% | 99.6% | 103.3% |
| 2014-09-01 | 101.4% | 99.1% | 103.4% | 103.2% | 98.3% | 103.9% | 103.0% | 101.6% | 101.6% | 116.0% | 104.6% | 97.8% | 104.2% | 103.1% | 97.0% | 100.6% | 102.0% | 100.4% | 98.3% | 106.1% | 99.4% | 104.2% | 104.3% | 95.8% | 103.2% | 95.3% | 99.2% | 100.7% | 102.8% | 101.6% | 100.7% | 101.0% | 100.8% | 99.4% | 103.5% | 111.7% | 95.3% | 104.5% | 101.7% | 100.0% | 97.6% | 104.5% | 103.3% | 99.9% | 113.2% | 102.4% | 99.1% | 104.3% | 102.1% | 98.4% | 99.7% | 103.3% |
| 2014-10-01 | 101.6% | 99.1% | 103.3% | 103.5% | 98.5% | 104.0% | 103.1% | 101.7% | 101.8% | 116.3% | 104.7% | 97.7% | 104.3% | 103.3% | 97.0% | 100.7% | 102.1% | 100.4% | 98.1% | 106.4% | 99.3% | 104.3% | 104.6% | 95.8% | 103.2% | 95.3% | 99.3% | 100.7% | 102.8% | 101.8% | 100.8% | 101.1% | 100.9% | 99.4% | 103.6% | 112.0% | 95.4% | 104.7% | 101.9% | 100.0% | 97.6% | 104.8% | 103.5% | 100.0% | 113.2% | 102.7% | 99.1% | 104.2% | 102.3% | 98.4% | 99.8% | 103.3% |
| 2014-11-01 | 101.7% | 99.1% | 103.2% | 103.7% | 98.6% | 104.1% | 103.1% | 101.7% | 101.9% | 116.5% | 104.7% | 97.7% | 104.4% | 103.5% | 96.9% | 100.8% | 102.1% | 100.4% | 97.9% | 106.5% | 99.2% | 104.3% | 104.7% | 95.7% | 103.3% | 95.4% | 99.4% | 100.8% | 102.8% | 101.9% | 101.0% | 101.1% | 101.0% | 99.4% | 103.7% | 112.1% | 95.4% | 104.9% | 101.9% | 100.1% | 97.6% | 105.1% | 103.5% | 100.1% | 113.2% | 102.9% | 99.1% | 104.1% | 102.5% | 98.4% | 99.8% | 103.2% |
| 2014-12-01 | 101.6% | 99.1% | 103.2% | 103.8% | 98.7% | 104.2% | 103.2% | 101.8% | 102.0% | 116.6% | 104.7% | 97.6% | 104.4% | 103.8% | 96.8% | 100.8% | 102.1% | 100.4% | 97.8% | 106.4% | 99.0% | 104.3% | 104.7% | 95.7% | 103.3% | 95.5% | 99.5% | 100.9% | 102.7% | 102.0% | 101.1% | 101.0% | 101.0% | 99.5% | 103.8% | 112.1% | 95.3% | 105.2% | 101.8% | 100.1% | 97.6% | 105.2% | 103.5% | 100.2% | 113.2% | 103.1% | 99.1% | 104.0% | 102.5% | 98.4% | 99.7% | 103.1% |
| 2015-01-01 | 102.0% | 99.3% | 103.1% | 104.0% | 98.7% | 104.2% | 103.2% | 101.8% | 102.1% | 116.7% | 104.7% | 97.5% | 104.5% | 104.0% | 96.8% | 100.8% | 102.1% | 100.4% | 97.7% | 106.3% | 98.9% | 104.4% | 104.7% | 95.6% | 103.3% | 95.7% | 99.6% | 101.0% | 102.6% | 102.1% | 101.1% | 101.0% | 101.1% | 99.5% | 103.9% | 112.0% | 95.2% | 105.4% | 101.8% | 100.1% | 97.7% | 105.4% | 103.6% | 100.2% | 113.1% | 103.3% | 99.0% | 104.0% | 102.5% | 98.3% | 99.7% | 103.0% |
| 2015-02-01 | 101.8% | 99.4% | 103.1% | 104.1% | 98.8% | 104.3% | 103.2% | 101.8% | 102.3% | 116.7% | 104.7% | 97.5% | 104.6% | 104.3% | 96.7% | 100.8% | 102.0% | 100.3% | 97.6% | 106.2% | 98.7% | 104.4% | 104.6% | 95.5% | 103.4% | 96.0% | 99.7% | 101.2% | 102.6% | 102.2% | 101.1% | 100.9% | 101.2% | 99.6% | 104.1% | 111.8% | 95.1% | 105.7% | 101.9% | 100.2% | 97.7% | 105.5% | 103.6% | 100.3% | 113.1% | 103.5% | 99.0% | 103.9% | 102.6% | 98.3% | 99.6% | 102.9% |
| 2015-03-01 | 101.8% | 99.6% | 103.1% | 104.2% | 98.9% | 104.3% | 103.3% | 101.8% | 102.5% | 116.9% | 104.8% | 97.5% | 104.6% | 104.6% | 96.8% | 100.9% | 102.0% | 100.3% | 97.5% | 106.1% | 98.6% | 104.5% | 104.6% | 95.5% | 103.5% | 96.2% | 99.7% | 101.4% | 102.5% | 102.3% | 101.1% | 100.9% | 101.3% | 99.7% | 104.3% | 111.5% | 95.0% | 106.0% | 102.0% | 100.3% | 97.7% | 105.7% | 103.6% | 100.4% | 113.1% | 103.8% | 98.9% | 103.9% | 102.7% | 98.3% | 99.6% | 102.9% |
| 2015-04-01 | 102.0% | 99.4% | 103.1% | 104.4% | 98.9% | 104.4% | 103.3% | 101.7% | 102.7% | 117.0% | 104.9% | 97.5% | 104.7% | 104.9% | 96.9% | 101.0% | 101.9% | 100.3% | 97.5% | 105.9% | 98.4% | 104.6% | 104.5% | 95.6% | 103.6% | 96.5% | 99.8% | 101.5% | 102.5% | 102.4% | 101.0% | 100.9% | 101.4% | 99.8% | 104.4% | 111.2% | 95.0% | 106.2% | 102.1% | 100.3% | 97.7% | 105.8% | 103.6% | 100.6% | 113.2% | 104.0% | 98.8% | 103.9% | 102.8% | 98.4% | 99.6% | 102.9% |
| 2015-05-01 | 102.4% | 99.1% | 103.0% | 104.5% | 99.0% | 104.4% | 103.4% | 101.5% | 102.9% | 117.2% | 105.0% | 97.5% | 104.8% | 105.2% | 97.0% | 101.1% | 101.8% | 100.3% | 97.4% | 105.7% | 98.2% | 104.6% | 104.5% | 95.6% | 103.8% | 96.6% | 99.8% | 101.5% | 102.6% | 102.5% | 100.9% | 100.8% | 101.4% | 99.8% | 104.6% | 111.0% | 94.9% | 106.3% | 102.4% | 100.4% | 97.6% | 105.9% | 103.6% | 100.7% | 113.3% | 104.3% | 98.6% | 103.8% | 103.0% | 98.4% | 99.6% | 103.0% |
| 2015-06-01 | 102.0% | 98.8% | 102.9% | 104.7% | 99.0% | 104.4% | 103.5% | 101.3% | 103.1% | 117.4% | 105.1% | 97.5% | 104.8% | 105.4% | 97.1% | 101.3% | 101.7% | 100.3% | 97.4% | 105.4% | 98.1% | 104.6% | 104.4% | 95.7% | 103.8% | 96.7% | 99.8% | 101.5% | 102.7% | 102.6% | 100.7% | 100.7% | 101.3% | 99.7% | 104.7% | 110.9% | 94.9% | 106.3% | 102.6% | 100.5% | 97.4% | 105.9% | 103.6% | 100.8% | 113.4% | 104.5% | 98.4% | 103.8% | 103.2% | 98.3% | 99.6% | 102.9% |
| 2015-07-01 | 102.0% | 98.5% | 102.8% | 104.8% | 99.0% | 104.3% | 103.6% | 101.1% | 103.3% | 117.6% | 105.2% | 97.4% | 104.9% | 105.5% | 97.1% | 101.4% | 101.6% | 100.3% | 97.3% | 105.1% | 97.9% | 104.6% | 104.3% | 95.7% | 103.8% | 96.8% | 99.7% | 101.5% | 102.7% | 102.6% | 100.6% | 100.6% | 101.2% | 99.7% | 104.8% | 110.8% | 94.8% | 106.2% | 102.8% | 100.5% | 97.2% | 105.9% | 103.6% | 100.9% | 113.5% | 104.7% | 98.2% | 103.7% | 103.3% | 98.1% | 99.6% | 102.7% |
| 2015-08-01 | 102.1% | 98.1% | 102.8% | 104.9% | 99.0% | 104.3% | 103.6% | 101.0% | 103.5% | 117.8% | 105.3% | 97.4% | 105.0% | 105.7% | 97.1% | 101.6% | 101.6% | 100.3% | 97.3% | 104.8% | 97.7% | 104.5% | 104.1% | 95.7% | 103.8% | 96.8% | 99.7% | 101.6% | 102.8% | 102.7% | 100.6% | 100.5% | 101.1% | 99.6% | 104.8% | 110.8% | 94.7% | 106.0% | 103.1% | 100.6% | 97.0% | 105.9% | 103.6% | 100.9% | 113.6% | 104.9% | 98.1% | 103.6% | 103.4% | 97.9% | 99.6% | 102.6% |
| 2015-09-01 | 101.8% | 97.8% | 102.7% | 105.0% | 99.0% | 104.3% | 103.8% | 100.9% | 103.7% | 117.9% | 105.5% | 97.3% | 105.1% | 105.8% | 97.2% | 101.8% | 101.6% | 100.3% | 97.4% | 104.6% | 97.6% | 104.5% | 104.1% | 95.8% | 103.9% | 97.0% | 99.7% | 101.7% | 102.9% | 102.7% | 100.6% | 100.5% | 101.1% | 99.5% | 104.9% | 110.8% | 94.7% | 106.0% | 103.3% | 100.6% | 96.9% | 105.9% | 103.6% | 101.0% | 113.7% | 105.1% | 98.0% | 103.5% | 103.6% | 97.7% | 99.7% | 102.5% |
| 2015-10-01 | 102.1% | 97.8% | 102.7% | 105.1% | 99.0% | 104.4% | 104.0% | 100.8% | 103.9% | 118.1% | 105.7% | 97.4% | 105.2% | 106.0% | 97.3% | 102.1% | 101.7% | 100.4% | 97.7% | 104.5% | 97.6% | 104.5% | 104.0% | 95.9% | 103.9% | 97.1% | 99.8% | 101.8% | 103.1% | 102.8% | 100.6% | 100.5% | 101.0% | 99.6% | 105.0% | 110.9% | 94.8% | 105.9% | 103.7% | 100.7% | 96.8% | 106.0% | 103.7% | 101.1% | 113.9% | 105.4% | 98.0% | 103.5% | 103.9% | 97.7% | 99.8% | 102.4% |
| 2015-11-01 | 102.3% | 97.5% | 102.7% | 105.4% | 99.1% | 104.5% | 104.3% | 100.9% | 104.1% | 118.3% | 105.9% | 97.6% | 105.4% | 106.2% | 97.6% | 102.5% | 101.9% | 100.5% | 97.9% | 104.5% | 97.7% | 104.6% | 104.1% | 96.2% | 104.1% | 97.3% | 99.9% | 102.0% | 103.2% | 102.9% | 100.8% | 100.5% | 101.1% | 99.7% | 105.2% | 111.1% | 95.0% | 106.0% | 104.1% | 100.9% | 96.8% | 106.2% | 103.8% | 101.3% | 114.1% | 105.7% | 98.0% | 103.6% | 104.2% | 97.7% | 100.0% | 102.4% |
| 2015-12-01 | 102.7% | 97.7% | 102.7% | 105.6% | 99.2% | 104.7% | 104.7% | 100.9% | 104.3% | 118.6% | 106.2% | 97.7% | 105.6% | 106.4% | 97.9% | 102.9% | 102.1% | 100.6% | 98.2% | 104.5% | 97.9% | 104.7% | 104.3% | 96.5% | 104.2% | 97.5% | 100.0% | 102.2% | 103.3% | 103.1% | 101.0% | 100.7% | 101.3% | 99.8% | 105.5% | 111.2% | 95.2% | 106.1% | 104.6% | 101.1% | 96.8% | 106.5% | 103.9% | 101.6% | 114.4% | 106.1% | 98.0% | 103.7% | 104.6% | 97.7% | 100.2% | 102.6% |
| 2016-01-01 | 102.8% | 98.0% | 102.8% | 105.9% | 99.3% | 104.9% | 105.0% | 101.0% | 104.5% | 118.8% | 106.4% | 97.9% | 105.7% | 106.7% | 98.1% | 103.3% | 102.3% | 100.6% | 98.4% | 104.5% | 98.1% | 104.7% | 104.5% | 96.7% | 104.4% | 97.6% | 100.1% | 102.3% | 103.4% | 103.2% | 101.2% | 100.8% | 101.4% | 99.9% | 105.7% | 111.3% | 95.5% | 106.2% | 105.0% | 101.2% | 96.8% | 106.7% | 104.0% | 101.8% | 114.7% | 106.4% | 98.1% | 103.7% | 104.9% | 97.8% | 100.4% | 102.8% |
| 2016-02-01 | 103.1% | 98.2% | 102.8% | 106.1% | 99.4% | 105.0% | 105.3% | 101.0% | 104.5% | 119.0% | 106.6% | 97.9% | 105.8% | 107.0% | 98.3% | 103.6% | 102.4% | 100.6% | 98.6% | 104.5% | 98.3% | 104.8% | 104.6% | 97.0% | 104.4% | 97.6% | 100.2% | 102.4% | 103.5% | 103.3% | 101.4% | 100.8% | 101.5% | 99.8% | 105.9% | 111.4% | 95.6% | 106.3% | 105.4% | 101.3% | 96.8% | 106.8% | 104.0% | 102.0% | 114.9% | 106.8% | 98.1% | 103.8% | 105.2% | 97.8% | 100.5% | 103.0% |
| 2016-03-01 | 103.4% | 98.3% | 102.8% | 106.3% | 99.4% | 105.1% | 105.5% | 101.1% | 104.5% | 119.2% | 106.7% | 98.8% | 105.9% | 107.2% | 98.3% | 103.7% | 102.4% | 100.6% | 98.7% | 104.4% | 98.5% | 104.8% | 104.7% | 97.2% | 104.4% | 97.5% | 100.2% | 102.4% | 103.5% | 103.4% | 101.5% | 100.8% | 101.6% | 99.8% | 106.1% | 111.5% | 95.7% | 106.2% | 105.7% | 101.3% | 96.9% | 106.9% | 104.1% | 102.2% | 115.1% | 107.1% | 98.2% | 103.8% | 105.5% | 97.7% | 100.6% | 103.0% |
| 2016-04-01 | 103.4% | 98.5% | 102.8% | 106.5% | 99.4% | 105.2% | 105.7% | 101.1% | 104.5% | 119.2% | 106.9% | 99.5% | 105.9% | 107.3% | 98.3% | 103.8% | 102.3% | 100.5% | 98.8% | 104.4% | 98.7% | 104.7% | 104.8% | 97.3% | 104.3% | 97.4% | 100.3% | 102.4% | 103.5% | 103.5% | 101.6% | 100.8% | 101.7% | 99.6% | 106.2% | 111.5% | 95.7% | 106.1% | 105.9% | 101.3% | 96.9% | 106.9% | 104.1% | 102.3% | 115.3% | 107.3% | 98.2% | 103.8% | 105.7% | 97.5% | 100.6% | 103.0% |
| 2016-05-01 | 103.2% | 98.6% | 102.8% | 106.7% | 99.3% | 105.3% | 105.9% | 101.2% | 104.5% | 119.3% | 107.1% | 100.3% | 106.0% | 107.5% | 98.1% | 103.8% | 102.2% | 100.3% | 99.0% | 104.3% | 98.9% | 104.8% | 104.9% | 97.4% | 104.3% | 97.4% | 100.4% | 102.4% | 103.4% | 103.6% | 101.7% | 100.7% | 101.8% | 99.5% | 106.2% | 111.5% | 95.7% | 106.0% | 106.0% | 101.3% | 97.0% | 106.8% | 104.1% | 102.5% | 115.5% | 107.6% | 98.2% | 103.9% | 105.9% | 97.4% | 100.6% | 102.8% |
| 2016-06-01 | 103.3% | 98.7% | 102.8% | 106.9% | 99.3% | 105.4% | 106.0% | 101.3% | 104.5% | 119.4% | 107.3% | 101.1% | 106.2% | 107.7% | 98.0% | 103.8% | 102.1% | 100.2% | 99.2% | 104.1% | 99.0% | 104.8% | 105.1% | 97.6% | 104.3% | 97.4% | 100.4% | 102.3% | 103.3% | 103.7% | 101.8% | 100.7% | 101.9% | 99.5% | 106.3% | 111.6% | 95.6% | 105.9% | 106.2% | 101.2% | 97.0% | 106.7% | 104.1% | 102.8% | 115.7% | 107.8% | 98.2% | 104.0% | 106.1% | 97.2% | 100.6% | 102.5% |
| 2016-07-01 | 103.4% | 98.8% | 102.8% | 107.1% | 99.3% | 105.5% | 106.3% | 101.4% | 104.5% | 119.5% | 107.5% | 101.9% | 106.4% | 107.9% | 97.8% | 103.7% | 102.0% | 100.2% | 99.5% | 104.0% | 99.1% | 105.0% | 105.2% | 97.7% | 104.3% | 97.5% | 100.4% | 102.3% | 103.2% | 103.9% | 101.8% | 100.7% | 102.0% | 99.5% | 106.5% | 111.6% | 95.6% | 105.9% | 106.3% | 101.2% | 97.0% | 106.7% | 104.1% | 103.0% | 115.9% | 108.1% | 98.3% | 104.2% | 106.2% | 97.1% | 100.6% | 102.2% |
| 2016-08-01 | 103.7% | 99.0% | 102.8% | 107.3% | 99.3% | 105.6% | 106.5% | 101.4% | 104.5% | 119.7% | 107.8% | 102.7% | 106.5% | 108.0% | 97.7% | 103.7% | 101.9% | 100.1% | 99.7% | 103.8% | 99.2% | 105.1% | 105.4% | 97.8% | 104.3% | 97.6% | 100.4% | 102.3% | 103.1% | 104.0% | 101.8% | 100.6% | 102.1% | 99.5% | 106.6% | 111.6% | 95.6% | 105.8% | 106.5% | 101.1% | 97.0% | 106.6% | 104.1% | 103.3% | 116.1% | 108.4% | 98.3% | 104.4% | 106.4% | 97.0% | 100.6% | 102.0% |
| 2016-09-01 | 103.8% | 99.1% | 102.8% | 107.5% | 99.3% | 105.7% | 106.7% | 101.5% | 104.5% | 119.9% | 108.0% | 103.1% | 106.7% | 108.2% | 97.5% | 103.5% | 101.8% | 100.0% | 99.9% | 103.7% | 99.4% | 105.3% | 105.5% | 97.9% | 104.4% | 97.7% | 100.3% | 102.4% | 103.1% | 104.2% | 101.8% | 100.6% | 102.1% | 99.5% | 106.8% | 111.5% | 95.6% | 105.8% | 106.6% | 101.0% | 97.0% | 106.6% | 104.1% | 103.4% | 116.2% | 108.6% | 98.3% | 104.6% | 106.5% | 96.9% | 100.6% | 101.8% |
| 2016-10-01 | 103.7% | 99.2% | 102.8% | 107.6% | 99.2% | 105.8% | 106.9% | 101.6% | 104.6% | 120.2% | 108.2% | 104.3% | 106.7% | 108.3% | 97.4% | 103.4% | 101.6% | 99.9% | 100.0% | 103.5% | 99.4% | 105.5% | 105.7% | 98.0% | 104.5% | 97.8% | 100.2% | 102.4% | 103.0% | 104.3% | 101.8% | 100.6% | 102.1% | 99.5% | 107.0% | 111.4% | 95.7% | 105.7% | 106.6% | 100.8% | 97.0% | 106.6% | 104.1% | 103.6% | 116.4% | 108.9% | 98.3% | 104.8% | 106.6% | 96.9% | 100.6% | 101.7% |
| 2016-11-01 | 103.6% | 99.3% | 102.9% | 107.8% | 99.2% | 105.8% | 107.0% | 101.8% | 104.7% | 120.4% | 108.4% | 104.3% | 106.7% | 108.5% | 97.2% | 103.2% | 101.4% | 99.8% | 100.2% | 103.3% | 99.5% | 105.6% | 105.8% | 98.0% | 104.5% | 97.9% | 100.1% | 102.4% | 102.9% | 104.5% | 101.7% | 100.5% | 102.1% | 99.5% | 107.1% | 111.3% | 95.8% | 105.7% | 106.7% | 100.7% | 97.1% | 106.7% | 104.1% | 103.6% | 116.5% | 109.2% | 98.3% | 104.9% | 106.7% | 96.9% | 100.5% | 101.6% |
| 2016-12-01 | 103.7% | 99.3% | 102.9% | 108.0% | 99.2% | 105.9% | 107.2% | 101.9% | 104.9% | 120.6% | 108.5% | 104.4% | 106.8% | 108.7% | 97.0% | 103.1% | 101.2% | 99.8% | 100.4% | 103.2% | 99.6% | 105.8% | 105.9% | 98.1% | 104.6% | 97.9% | 99.9% | 102.4% | 102.8% | 104.7% | 101.7% | 100.4% | 102.1% | 99.5% | 107.3% | 111.2% | 95.9% | 105.6% | 106.7% | 100.6% | 97.1% | 106.7% | 104.1% | 103.7% | 116.7% | 109.5% | 98.4% | 105.1% | 106.9% | 96.8% | 100.5% | 101.4% |
| 2017-01-01 | 103.7% | 100.7% | 102.8% | 105.5% | 99.1% | 106.0% | 106.8% | 103.0% | 105.0% | 118.0% | 108.0% | 104.5% | 109.1% | 109.6% | 97.9% | 103.2% | 101.6% | 100.0% | 100.8% | 103.2% | 100.2% | 107.2% | 107.2% | 98.5% | 105.4% | 97.8% | 99.7% | 103.0% | 103.5% | 104.5% | 102.1% | 103.3% | 102.3% | 102.3% | 106.1% | 112.5% | 96.3% | 105.3% | 106.6% | 101.6% | 99.2% | 105.2% | 103.8% | 104.0% | 116.1% | 110.4% | 100.6% | 105.8% | 107.1% | 96.9% | 101.1% | 100.6% |
| 2017-02-01 | 103.9% | 100.8% | 102.8% | 105.7% | 99.2% | 106.1% | 107.1% | 103.2% | 105.2% | 118.3% | 108.3% | 104.6% | 109.2% | 109.9% | 97.8% | 103.2% | 101.5% | 100.0% | 101.0% | 103.2% | 100.3% | 107.4% | 107.5% | 98.5% | 105.6% | 97.8% | 99.7% | 103.2% | 103.5% | 104.8% | 102.2% | 103.3% | 102.4% | 102.4% | 106.2% | 112.7% | 96.5% | 105.3% | 106.9% | 101.6% | 99.3% | 105.3% | 103.9% | 104.1% | 116.3% | 110.7% | 100.7% | 106.1% | 107.3% | 96.8% | 101.2% | 100.4% |
| 2017-03-01 | 104.0% | 100.8% | 102.8% | 105.9% | 99.4% | 106.2% | 107.5% | 103.3% | 105.4% | 118.5% | 108.6% | 104.7% | 109.3% | 110.2% | 97.8% | 103.3% | 101.6% | 100.0% | 101.2% | 103.2% | 100.4% | 107.6% | 107.7% | 98.5% | 105.8% | 97.9% | 99.7% | 103.4% | 103.6% | 105.1% | 102.3% | 103.4% | 102.5% | 102.6% | 106.4% | 112.8% | 96.6% | 105.4% | 107.2% | 101.7% | 99.4% | 105.4% | 104.0% | 104.2% | 116.5% | 111.1% | 100.8% | 106.3% | 107.6% | 96.8% | 101.4% | 100.3% |
| 2017-04-01 | 104.2% | 100.8% | 102.7% | 106.2% | 99.6% | 106.3% | 107.9% | 103.4% | 105.6% | 118.7% | 108.8% | 104.9% | 109.4% | 110.5% | 97.8% | 103.4% | 101.7% | 100.1% | 101.3% | 103.2% | 100.5% | 107.8% | 107.9% | 98.5% | 105.9% | 97.9% | 99.7% | 103.6% | 103.8% | 105.4% | 102.4% | 103.5% | 102.5% | 102.8% | 106.5% | 112.9% | 96.7% | 105.5% | 107.6% | 101.7% | 99.4% | 105.5% | 104.1% | 104.4% | 116.6% | 111.4% | 100.9% | 106.5% | 107.8% | 96.9% | 101.5% | 100.2% |
| 2017-05-01 | 104.0% | 100.8% | 102.7% | 106.4% | 99.7% | 106.4% | 108.3% | 103.3% | 105.8% | 119.0% | 109.0% | 105.1% | 109.3% | 110.8% | 97.8% | 103.6% | 101.8% | 100.1% | 101.4% | 103.2% | 100.6% | 107.9% | 108.1% | 98.6% | 106.1% | 97.9% | 99.7% | 103.7% | 103.9% | 105.7% | 102.5% | 103.6% | 102.5% | 103.0% | 106.7% | 112.9% | 96.8% | 105.7% | 108.0% | 101.7% | 99.5% | 105.6% | 104.2% | 104.6% | 116.8% | 111.7% | 101.0% | 106.7% | 108.1% | 97.0% | 101.7% | 100.1% |
| 2017-06-01 | 104.1% | 100.9% | 102.6% | 106.5% | 99.8% | 106.5% | 108.7% | 103.2% | 106.0% | 119.2% | 109.1% | 105.3% | 109.1% | 111.2% | 97.8% | 103.7% | 101.8% | 100.2% | 101.4% | 103.2% | 100.6% | 108.1% | 108.3% | 98.8% | 106.1% | 97.9% | 99.7% | 103.9% | 104.0% | 105.9% | 102.5% | 103.6% | 102.5% | 103.1% | 107.0% | 112.8% | 96.9% | 105.9% | 108.3% | 101.6% | 99.5% | 105.7% | 104.3% | 104.8% | 116.9% | 112.0% | 101.0% | 106.8% | 108.4% | 97.1% | 101.8% | 100.1% |
| 2017-07-01 | 104.3% | 100.9% | 102.5% | 106.7% | 99.9% | 106.6% | 109.1% | 103.1% | 106.2% | 119.3% | 109.1% | 105.4% | 108.9% | 111.5% | 97.9% | 103.7% | 101.8% | 100.2% | 101.4% | 103.1% | 100.6% | 108.3% | 108.4% | 98.9% | 106.2% | 97.8% | 99.7% | 103.9% | 104.2% | 106.2% | 102.5% | 103.6% | 102.4% | 103.2% | 107.2% | 112.6% | 97.0% | 106.1% | 108.4% | 101.5% | 99.6% | 105.8% | 104.4% | 105.0% | 117.0% | 112.2% | 101.0% | 106.9% | 108.6% | 97.3% | 101.9% | 100.1% |
| 2017-08-01 | 104.3% | 101.0% | 102.3% | 106.8% | 99.9% | 106.6% | 109.4% | 102.9% | 106.3% | 119.4% | 109.1% | 105.5% | 108.6% | 111.8% | 97.9% | 103.8% | 101.8% | 100.1% | 101.4% | 103.1% | 100.6% | 108.4% | 108.5% | 99.0% | 106.2% | 97.7% | 99.6% | 103.9% | 104.2% | 106.4% | 102.5% | 103.6% | 102.3% | 103.2% | 107.4% | 112.4% | 97.0% | 106.2% | 108.4% | 101.4% | 99.6% | 105.8% | 104.4% | 105.1% | 117.0% | 112.4% | 101.0% | 106.9% | 108.8% | 97.4% | 101.9% | 100.1% |
| 2017-09-01 | 104.7% | 101.0% | 102.2% | 106.9% | 99.8% | 106.6% | 109.6% | 102.7% | 106.4% | 119.4% | 109.1% | 105.6% | 108.3% | 112.1% | 97.9% | 103.8% | 101.7% | 100.0% | 101.3% | 103.1% | 100.5% | 108.4% | 108.6% | 99.1% | 106.2% | 97.5% | 99.6% | 103.9% | 104.2% | 106.7% | 102.5% | 103.4% | 102.1% | 103.1% | 107.5% | 112.2% | 96.9% | 106.2% | 108.4% | 101.3% | 99.7% | 105.8% | 104.3% | 105.3% | 117.1% | 112.5% | 101.0% | 106.9% | 108.9% | 97.5% | 101.8% | 100.0% |
| 2017-10-01 | 104.2% | 101.0% | 102.0% | 107.0% | 99.7% | 106.5% | 109.8% | 102.6% | 106.4% | 119.4% | 109.1% | 105.6% | 108.1% | 112.3% | 97.9% | 103.7% | 101.6% | 99.8% | 101.2% | 103.1% | 100.3% | 108.3% | 108.7% | 99.1% | 106.2% | 97.4% | 99.5% | 103.8% | 104.2% | 107.0% | 102.5% | 103.3% | 102.0% | 102.9% | 107.5% | 112.1% | 96.7% | 106.2% | 108.3% | 101.2% | 99.7% | 105.7% | 104.2% | 105.3% | 117.2% | 112.6% | 101.0% | 106.9% | 109.0% | 97.5% | 101.7% | 99.8% |
| 2017-11-01 | 104.3% | 101.1% | 101.8% | 107.2% | 99.6% | 106.4% | 110.0% | 102.5% | 106.4% | 119.4% | 109.2% | 105.5% | 108.0% | 112.5% | 97.9% | 103.8% | 101.5% | 99.7% | 101.1% | 103.1% | 100.1% | 108.3% | 108.8% | 99.0% | 106.2% | 97.3% | 99.4% | 103.8% | 104.2% | 107.3% | 102.5% | 103.1% | 102.0% | 102.7% | 107.4% | 112.0% | 96.5% | 106.2% | 108.2% | 101.2% | 99.7% | 105.6% | 104.2% | 105.4% | 117.3% | 112.6% | 101.0% | 106.9% | 109.0% | 97.5% | 101.5% | 99.7% |
| 2017-12-01 | 104.3% | 101.3% | 101.6% | 107.4% | 99.5% | 106.4% | 110.2% | 102.4% | 106.4% | 119.5% | 109.3% | 105.5% | 108.0% | 112.7% | 97.9% | 103.9% | 101.5% | 99.6% | 101.0% | 103.2% | 100.0% | 108.2% | 109.0% | 99.0% | 106.2% | 97.2% | 99.3% | 103.8% | 104.2% | 107.6% | 102.6% | 103.0% | 101.9% | 102.6% | 107.3% | 112.0% | 96.3% | 106.3% | 108.1% | 101.2% | 99.7% | 105.5% | 104.2% | 105.5% | 117.5% | 112.7% | 101.0% | 106.9% | 109.1% | 97.6% | 101.4% | 99.6% |
| 2018-01-01 | 104.6% | 101.5% | 101.4% | 107.6% | 99.5% | 106.5% | 110.5% | 102.5% | 106.5% | 119.6% | 109.5% | 105.4% | 108.2% | 112.9% | 97.9% | 104.1% | 101.6% | 99.6% | 101.0% | 103.4% | 100.0% | 108.1% | 109.4% | 99.0% | 106.2% | 97.3% | 99.3% | 103.9% | 104.3% | 108.0% | 102.8% | 102.9% | 102.0% | 102.5% | 107.4% | 112.0% | 96.3% | 106.3% | 108.1% | 101.2% | 99.8% | 105.4% | 104.2% | 105.6% | 117.7% | 112.9% | 101.1% | 107.0% | 109.3% | 97.6% | 101.4% | 99.5% |
| 2018-02-01 | 105.2% | 101.8% | 101.3% | 108.0% | 99.6% | 106.6% | 110.8% | 102.6% | 106.8% | 119.9% | 109.7% | 105.5% | 108.5% | 113.2% | 97.9% | 104.4% | 101.9% | 99.7% | 101.1% | 103.6% | 100.0% | 108.1% | 109.8% | 99.1% | 106.3% | 97.4% | 99.4% | 104.1% | 104.4% | 108.4% | 103.0% | 103.0% | 102.1% | 102.6% | 107.5% | 112.0% | 96.3% | 106.5% | 108.1% | 101.3% | 99.9% | 105.5% | 104.3% | 105.9% | 118.0% | 113.1% | 101.2% | 107.2% | 109.6% | 97.8% | 101.5% | 99.5% |
| 2018-03-01 | 105.1% | 102.1% | 101.3% | 108.3% | 99.7% | 106.8% | 111.2% | 102.9% | 107.0% | 120.2% | 109.9% | 105.6% | 108.8% | 113.5% | 97.9% | 104.9% | 102.2% | 99.9% | 101.3% | 103.8% | 100.2% | 108.2% | 110.2% | 99.3% | 106.4% | 97.5% | 99.4% | 104.3% | 104.7% | 108.8% | 103.4% | 103.1% | 102.3% | 102.7% | 107.7% | 112.1% | 96.5% | 106.6% | 108.1% | 101.5% | 100.0% | 105.6% | 104.5% | 106.3% | 118.3% | 113.4% | 101.4% | 107.4% | 110.0% | 98.1% | 101.5% | 99.6% |
| 2018-04-01 | 105.1% | 102.4% | 101.3% | 108.7% | 99.7% | 107.0% | 111.6% | 103.1% | 107.2% | 120.4% | 110.2% | 105.7% | 109.0% | 113.8% | 98.0% | 105.3% | 102.5% | 100.0% | 101.5% | 103.9% | 100.4% | 108.3% | 110.6% | 99.4% | 106.4% | 97.6% | 99.5% | 104.5% | 104.9% | 109.1% | 103.7% | 103.3% | 102.4% | 102.9% | 107.9% | 112.0% | 96.6% | 106.6% | 108.1% | 101.6% | 100.2% | 105.8% | 104.7% | 106.6% | 118.6% | 113.7% | 101.5% | 107.6% | 110.3% | 98.3% | 101.6% | 99.7% |
| 2018-05-01 | 105.2% | 102.5% | 101.2% | 109.0% | 99.8% | 107.1% | 111.9% | 103.3% | 107.3% | 120.3% | 110.3% | 105.6% | 109.0% | 114.0% | 98.0% | 105.6% | 102.7% | 100.1% | 101.5% | 103.8% | 100.5% | 108.4% | 110.9% | 99.4% | 106.5% | 97.6% | 99.5% | 104.7% | 105.0% | 109.3% | 103.9% | 103.4% | 102.5% | 102.9% | 108.0% | 111.8% | 96.7% | 106.5% | 108.0% | 101.7% | 100.3% | 106.0% | 104.7% | 106.8% | 118.7% | 113.9% | 101.5% | 107.5% | 110.5% | 98.5% | 101.5% | 99.8% |
| 2018-06-01 | 105.4% | 102.6% | 101.1% | 109.3% | 99.8% | 107.1% | 112.1% | 103.5% | 107.2% | 120.0% | 110.4% | 105.5% | 108.8% | 114.3% | 97.9% | 105.7% | 102.8% | 100.1% | 101.5% | 103.6% | 100.6% | 108.5% | 111.0% | 99.4% | 106.4% | 97.5% | 99.4% | 104.8% | 105.1% | 109.4% | 103.9% | 103.4% | 102.5% | 103.0% | 108.1% | 111.6% | 96.8% | 106.4% | 107.9% | 101.7% | 100.3% | 106.2% | 104.7% | 107.0% | 118.8% | 114.1% | 101.5% | 107.4% | 110.7% | 98.5% | 101.4% | 99.8% |
| 2018-07-01 | 105.4% | 102.7% | 101.0% | 109.6% | 99.8% | 107.1% | 112.2% | 103.6% | 107.0% | 119.6% | 110.5% | 105.4% | 108.5% | 114.4% | 97.9% | 105.7% | 102.9% | 100.0% | 101.4% | 103.4% | 100.5% | 108.5% | 111.1% | 99.4% | 106.4% | 97.3% | 99.3% | 104.8% | 105.2% | 109.6% | 103.9% | 103.4% | 102.4% | 102.9% | 108.1% | 111.4% | 96.7% | 106.2% | 107.9% | 101.7% | 100.3% | 106.4% | 104.7% | 107.1% | 118.8% | 114.1% | 101.4% | 107.3% | 110.9% | 98.5% | 101.2% | 99.8% |
| 2018-08-01 | 105.0% | 102.8% | 100.8% | 109.9% | 99.8% | 107.0% | 112.2% | 103.7% | 106.9% | 119.3% | 110.6% | 105.3% | 108.1% | 114.6% | 97.9% | 105.6% | 102.9% | 100.0% | 101.3% | 103.1% | 100.4% | 108.6% | 111.1% | 99.4% | 106.4% | 97.2% | 99.2% | 104.9% | 105.2% | 109.8% | 103.9% | 103.3% | 102.4% | 102.9% | 108.1% | 111.2% | 96.7% | 106.0% | 107.9% | 101.8% | 100.2% | 106.6% | 104.6% | 107.2% | 118.8% | 114.2% | 101.2% | 107.2% | 111.1% | 98.5% | 101.0% | 99.8% |
| 2018-09-01 | 105.3% | 102.9% | 100.6% | 110.2% | 99.9% | 107.0% | 112.3% | 103.7% | 106.8% | 119.2% | 110.6% | 105.2% | 107.8% | 114.8% | 97.9% | 105.4% | 103.0% | 100.0% | 101.2% | 103.0% | 100.3% | 108.7% | 111.1% | 99.4% | 106.5% | 97.1% | 99.2% | 104.9% | 105.3% | 110.1% | 103.9% | 103.3% | 102.5% | 102.9% | 108.2% | 111.2% | 96.7% | 105.9% | 108.0% | 101.8% | 100.1% | 106.8% | 104.5% | 107.3% | 118.9% | 114.3% | 101.1% | 107.2% | 111.3% | 98.5% | 100.8% | 99.8% |
| 2018-10-01 | 105.6% | 103.1% | 100.5% | 110.6% | 100.1% | 107.1% | 112.4% | 103.8% | 106.9% | 119.3% | 110.7% | 105.2% | 107.5% | 115.0% | 98.0% | 105.4% | 103.0% | 100.0% | 101.1% | 102.9% | 100.3% | 108.9% | 111.1% | 99.5% | 106.7% | 97.1% | 99.3% | 105.0% | 105.5% | 110.5% | 103.9% | 103.3% | 102.7% | 102.9% | 108.3% | 111.3% | 96.8% | 105.9% | 108.2% | 101.9% | 100.0% | 107.1% | 104.6% | 107.5% | 119.0% | 114.4% | 101.0% | 107.4% | 111.6% | 98.5% | 100.8% | 99.8% |
| 2018-11-01 | 105.7% | 103.3% | 100.4% | 110.9% | 100.3% | 107.1% | 112.5% | 103.9% | 107.1% | 119.6% | 110.8% | 105.3% | 107.3% | 115.3% | 98.1% | 105.4% | 103.2% | 100.0% | 101.2% | 103.0% | 100.2% | 109.1% | 111.2% | 99.6% | 106.9% | 97.2% | 99.4% | 105.2% | 105.6% | 111.0% | 104.0% | 103.4% | 102.9% | 102.9% | 108.5% | 111.6% | 96.9% | 105.9% | 108.4% | 102.1% | 100.0% | 107.3% | 104.7% | 107.8% | 119.1% | 114.6% | 101.0% | 107.7% | 112.0% | 98.5% | 100.8% | 99.8% |
| 2018-12-01 | 106.0% | 103.6% | 100.3% | 111.2% | 100.5% | 107.2% | 112.7% | 104.0% | 107.4% | 120.0% | 110.9% | 105.4% | 107.2% | 115.7% | 98.2% | 105.5% | 103.5% | 100.1% | 101.2% | 103.2% | 100.1% | 109.3% | 111.3% | 99.7% | 107.1% | 97.3% | 99.6% | 105.3% | 105.8% | 111.5% | 104.2% | 103.5% | 103.2% | 103.0% | 108.8% | 111.9% | 97.0% | 106.0% | 108.6% | 102.2% | 99.9% | 107.6% | 104.9% | 108.1% | 119.2% | 114.9% | 101.0% | 108.0% | 112.5% | 98.5% | 100.8% | 99.7% |
| 2019-01-01 | 105.9% | 103.8% | 100.2% | 111.4% | 100.7% | 107.3% | 112.9% | 104.0% | 107.7% | 120.4% | 111.0% | 105.5% | 107.2% | 116.0% | 98.3% | 105.5% | 103.7% | 100.1% | 101.3% | 103.3% | 100.0% | 109.5% | 111.3% | 99.8% | 107.2% | 97.4% | 99.7% | 105.4% | 105.9% | 112.0% | 104.3% | 103.7% | 103.4% | 103.0% | 109.0% | 112.2% | 97.0% | 106.2% | 108.8% | 102.4% | 99.8% | 107.9% | 105.0% | 108.5% | 119.4% | 115.1% | 101.0% | 108.4% | 112.9% | 98.4% | 100.8% | 99.7% |
| 2019-02-01 | 106.0% | 103.9% | 100.1% | 111.6% | 100.8% | 107.3% | 113.1% | 104.1% | 107.9% | 120.8% | 111.1% | 105.6% | 107.2% | 116.3% | 98.4% | 105.5% | 104.0% | 100.2% | 101.4% | 103.3% | 99.8% | 109.6% | 111.4% | 99.9% | 107.3% | 97.5% | 99.8% | 105.5% | 106.0% | 112.3% | 104.4% | 103.9% | 103.6% | 103.1% | 109.2% | 112.4% | 97.1% | 106.3% | 108.8% | 102.5% | 99.7% | 108.2% | 105.1% | 108.9% | 119.5% | 115.4% | 101.0% | 108.7% | 113.2% | 98.4% | 100.8% | 99.7% |
| 2019-03-01 | 105.9% | 104.0% | 100.1% | 111.9% | 100.8% | 107.3% | 113.2% | 104.1% | 108.0% | 121.0% | 111.2% | 105.6% | 107.2% | 116.6% | 98.3% | 105.4% | 104.2% | 100.3% | 101.6% | 103.3% | 99.8% | 109.8% | 111.4% | 99.9% | 107.4% | 97.7% | 99.8% | 105.6% | 106.1% | 112.6% | 104.5% | 104.1% | 103.7% | 103.1% | 109.4% | 112.5% | 97.1% | 106.4% | 108.8% | 102.5% | 99.7% | 108.4% | 105.3% | 109.2% | 119.6% | 115.6% | 101.0% | 108.9% | 113.5% | 98.3% | 100.9% | 99.7% |
| 2019-04-01 | 105.7% | 104.0% | 100.1% | 112.2% | 100.8% | 107.4% | 113.4% | 104.1% | 108.2% | 121.1% | 111.5% | 105.7% | 107.2% | 117.0% | 98.3% | 105.3% | 104.5% | 100.3% | 101.7% | 103.2% | 99.7% | 110.0% | 111.5% | 100.0% | 107.5% | 97.8% | 99.8% | 105.8% | 106.2% | 112.7% | 104.6% | 104.3% | 103.8% | 103.1% | 109.5% | 112.5% | 97.3% | 106.5% | 108.8% | 102.5% | 99.7% | 108.5% | 105.4% | 109.4% | 119.7% | 115.9% | 101.0% | 109.0% | 113.8% | 98.3% | 100.9% | 99.8% |
| 2019-05-01 | 105.8% | 104.0% | 100.2% | 112.4% | 100.8% | 107.4% | 113.6% | 104.2% | 108.2% | 121.2% | 111.7% | 105.9% | 107.2% | 117.3% | 98.2% | 105.2% | 104.7% | 100.4% | 101.9% | 103.0% | 99.8% | 110.2% | 111.5% | 100.0% | 107.7% | 98.0% | 99.9% | 106.0% | 106.3% | 112.8% | 104.7% | 104.6% | 103.9% | 103.1% | 109.6% | 112.4% | 97.4% | 106.6% | 108.8% | 102.5% | 99.9% | 108.6% | 105.5% | 109.6% | 119.9% | 116.1% | 100.9% | 109.1% | 114.0% | 98.4% | 101.0% | 99.9% |
| 2019-06-01 | 105.9% | 104.0% | 100.3% | 112.7% | 100.7% | 107.5% | 113.7% | 104.3% | 108.3% | 121.3% | 112.0% | 106.0% | 107.2% | 117.7% | 98.0% | 105.2% | 104.9% | 100.5% | 102.1% | 103.0% | 99.9% | 110.5% | 111.5% | 100.1% | 107.9% | 98.2% | 100.0% | 106.2% | 106.5% | 112.9% | 104.9% | 104.9% | 103.9% | 103.2% | 109.8% | 112.3% | 97.6% | 106.7% | 108.8% | 102.6% | 100.1% | 108.5% | 105.6% | 109.7% | 120.2% | 116.4% | 100.9% | 109.1% | 114.2% | 98.6% | 101.0% | 100.1% |
| 2019-07-01 | 106.2% | 104.0% | 100.4% | 113.0% | 100.8% | 107.6% | 113.8% | 104.5% | 108.3% | 121.2% | 112.2% | 106.2% | 107.1% | 118.1% | 97.9% | 105.3% | 105.1% | 100.7% | 102.2% | 102.9% | 100.1% | 110.9% | 111.5% | 100.1% | 108.1% | 98.3% | 100.1% | 106.5% | 106.7% | 113.1% | 105.0% | 105.2% | 103.9% | 103.2% | 110.0% | 112.2% | 97.7% | 106.7% | 108.9% | 102.6% | 100.4% | 108.4% | 105.7% | 109.7% | 120.4% | 116.6% | 100.9% | 109.1% | 114.4% | 98.8% | 101.0% | 100.4% |
| 2019-08-01 | 106.4% | 104.1% | 100.4% | 113.3% | 100.9% | 107.7% | 113.9% | 104.6% | 108.3% | 121.2% | 112.4% | 106.3% | 107.0% | 118.4% | 97.8% | 105.4% | 105.2% | 100.8% | 102.4% | 103.0% | 100.3% | 111.2% | 111.4% | 100.1% | 108.3% | 98.4% | 100.3% | 106.7% | 106.8% | 113.4% | 105.1% | 105.5% | 103.9% | 103.3% | 110.1% | 112.2% | 97.8% | 106.8% | 108.9% | 102.7% | 100.6% | 108.3% | 105.8% | 109.7% | 120.7% | 116.8% | 101.0% | 109.2% | 114.7% | 98.9% | 101.0% | 100.5% |
| 2019-09-01 | 106.6% | 104.2% | 100.3% | 113.6% | 101.0% | 107.8% | 114.1% | 104.7% | 108.2% | 121.3% | 112.6% | 106.4% | 106.9% | 118.7% | 97.7% | 105.5% | 105.3% | 100.9% | 102.5% | 103.1% | 100.4% | 111.5% | 111.4% | 100.1% | 108.5% | 98.3% | 100.5% | 107.0% | 107.0% | 113.7% | 105.3% | 105.7% | 104.0% | 103.4% | 110.3% | 112.2% | 97.9% | 106.9% | 108.9% | 102.8% | 100.8% | 108.3% | 105.8% | 109.7% | 120.9% | 117.1% | 101.1% | 109.4% | 115.0% | 99.0% | 101.0% | 100.7% |
| 2019-10-01 | 106.8% | 104.2% | 100.2% | 113.8% | 101.1% | 108.0% | 114.2% | 104.8% | 108.1% | 121.5% | 112.8% | 106.6% | 107.0% | 119.0% | 97.6% | 105.7% | 105.3% | 101.0% | 102.5% | 103.3% | 100.5% | 111.7% | 111.3% | 100.0% | 108.7% | 98.3% | 100.7% | 107.2% | 107.1% | 114.1% | 105.3% | 105.9% | 104.2% | 103.6% | 110.4% | 112.3% | 98.0% | 106.9% | 108.9% | 102.9% | 100.9% | 108.3% | 105.9% | 109.8% | 121.1% | 117.3% | 101.3% | 109.6% | 115.2% | 99.1% | 100.9% | 100.8% |
| 2019-11-01 | 106.8% | 104.3% | 100.2% | 114.1% | 101.2% | 108.2% | 114.4% | 104.9% | 108.0% | 121.9% | 112.9% | 106.7% | 107.1% | 119.3% | 97.5% | 105.7% | 105.2% | 101.0% | 102.6% | 103.4% | 100.5% | 111.9% | 111.2% | 99.9% | 108.9% | 98.2% | 100.9% | 107.4% | 107.2% | 114.4% | 105.4% | 106.1% | 104.4% | 103.7% | 110.5% | 112.3% | 98.2% | 106.9% | 108.8% | 102.9% | 101.0% | 108.4% | 105.9% | 109.9% | 121.2% | 117.5% | 101.4% | 109.7% | 115.4% | 99.2% | 100.9% | 101.0% |
| 2019-12-01 | 107.0% | 104.2% | 100.2% | 114.4% | 101.2% | 108.3% | 114.6% | 104.9% | 107.7% | 122.3% | 113.0% | 106.9% | 107.2% | 119.4% | 97.4% | 105.6% | 105.0% | 101.1% | 102.5% | 103.4% | 100.4% | 112.2% | 111.0% | 99.8% | 109.1% | 98.1% | 100.9% | 107.6% | 107.1% | 114.4% | 105.2% | 106.2% | 104.6% | 103.8% | 110.5% | 112.1% | 98.3% | 106.8% | 108.8% | 102.8% | 100.9% | 108.4% | 105.9% | 109.9% | 121.3% | 117.7% | 101.3% | 109.8% | 115.5% | 99.2% | 100.7% | 101.1% |
| 2020-01-01 | 106.9% | 104.1% | 100.1% | 114.5% | 101.2% | 108.4% | 114.5% | 104.7% | 107.4% | 122.6% | 112.8% | 106.9% | 107.3% | 119.5% | 97.3% | 105.4% | 104.6% | 101.0% | 102.2% | 103.1% | 100.2% | 112.3% | 110.7% | 99.5% | 109.3% | 97.9% | 100.8% | 107.5% | 106.9% | 114.4% | 104.9% | 106.1% | 104.7% | 103.7% | 110.4% | 112.0% | 98.3% | 106.6% | 108.6% | 102.6% | 100.6% | 108.3% | 105.7% | 109.8% | 121.2% | 117.7% | 101.2% | 109.7% | 115.6% | 99.1% | 100.5% | 101.2% |
| 2020-02-01 | 106.9% | 103.8% | 99.9% | 114.4% | 101.0% | 108.3% | 114.4% | 104.4% | 107.1% | 122.6% | 112.4% | 106.8% | 107.2% | 119.4% | 97.3% | 105.1% | 104.2% | 100.7% | 101.9% | 102.8% | 99.8% | 112.4% | 110.1% | 99.1% | 109.3% | 97.7% | 100.7% | 107.3% | 106.7% | 114.4% | 104.5% | 105.8% | 104.6% | 103.5% | 110.3% | 111.9% | 98.2% | 106.4% | 108.4% | 102.4% | 100.2% | 108.1% | 105.3% | 109.5% | 121.0% | 117.6% | 100.9% | 109.6% | 115.6% | 99.0% | 100.2% | 101.2% |
| 2020-03-01 | 105.7% | 103.6% | 99.7% | 114.2% | 102.4% | 106.8% | 116.6% | 104.1% | 108.3% | 121.9% | 111.7% | 106.8% | 107.1% | 119.0% | 96.5% | 102.6% | 103.7% | 100.4% | 101.4% | 104.3% | 99.4% | 112.3% | 109.3% | 98.6% | 109.1% | 97.5% | 100.7% | 107.0% | 107.2% | 113.8% | 104.0% | 105.3% | 103.1% | 103.1% | 105.6% | 111.9% | 96.7% | 106.1% | 108.2% | 102.1% | 99.6% | 107.9% | 105.1% | 109.1% | 120.0% | 117.4% | 100.8% | 109.7% | 114.9% | 98.7% | 99.9% | 101.0% |
| 2020-04-01 | 101.6% | 100.3% | 95.9% | 111.6% | 102.0% | 103.4% | 110.7% | 98.5% | 104.8% | 117.7% | 102.4% | 101.7% | 100.9% | 117.1% | 95.0% | 99.9% | 103.1% | 99.8% | 100.9% | 97.3% | 93.4% | 106.7% | 101.0% | 91.7% | 104.7% | 92.4% | 95.6% | 105.7% | 106.2% | 104.6% | 100.5% | 101.2% | 97.2% | 97.8% | 102.1% | 112.4% | 92.0% | 104.7% | 105.4% | 99.3% | 95.7% | 107.9% | 105.0% | 105.3% | 114.4% | 116.7% | 103.3% | 108.8% | 117.7% | 94.6% | 99.8% | 98.2% |
| 2020-05-01 | 102.7% | 104.0% | 98.1% | 112.9% | 100.9% | 103.2% | 113.9% | 102.5% | 110.0% | 115.2% | 109.6% | 103.8% | 103.3% | 118.3% | 95.1% | 102.1% | 100.3% | 100.1% | 101.4% | 99.2% | 95.6% | 106.9% | 108.0% | 98.0% | 106.8% | 93.3% | 93.7% | 106.3% | 106.2% | 100.1% | 102.2% | 102.6% | 97.5% | 99.2% | 105.0% | 111.2% | 93.9% | 105.8% | 109.5% | 100.9% | 99.8% | 108.4% | 105.2% | 107.2% | 119.7% | 117.4% | 97.9% | 106.8% | 115.6% | 96.3% | 100.3% | 101.6% |
| 2020-06-01 | 103.8% | 104.3% | 98.4% | 112.7% | 100.0% | 105.6% | 114.1% | 102.2% | 111.2% | 115.3% | 108.7% | 102.6% | 103.3% | 118.1% | 94.4% | 102.3% | 98.9% | 99.5% | 95.0% | 99.4% | 94.3% | 106.2% | 109.5% | 100.4% | 110.2% | 93.5% | 97.0% | 105.8% | 105.7% | 109.2% | 101.9% | 103.5% | 97.3% | 99.9% | 105.1% | 110.8% | 94.0% | 105.6% | 109.4% | 100.9% | 99.8% | 108.2% | 104.8% | 106.9% | 119.5% | 117.2% | 96.0% | 106.1% | 114.2% | 96.1% | 100.1% | 100.2% |
| 2020-07-01 | 104.0% | 104.8% | 99.4% | 113.2% | 100.0% | 105.7% | 110.3% | 102.6% | 107.0% | 116.1% | 111.6% | 102.4% | 105.1% | 118.6% | 94.6% | 103.1% | 98.7% | 100.0% | 97.1% | 100.5% | 95.4% | 106.3% | 109.8% | 99.3% | 109.5% | 94.2% | 100.6% | 106.1% | 105.8% | 110.8% | 102.4% | 105.7% | 97.8% | 100.1% | 106.0% | 111.3% | 94.7% | 106.2% | 110.1% | 101.5% | 100.4% | 108.9% | 105.4% | 107.5% | 120.4% | 117.8% | 95.2% | 106.4% | 113.9% | 96.6% | 100.5% | 99.9% |
| 2020-08-01 | 104.4% | 104.7% | 96.8% | 113.3% | 99.5% | 104.6% | 111.1% | 100.9% | 108.3% | 116.4% | 110.2% | 101.9% | 105.1% | 118.7% | 93.9% | 103.2% | 98.6% | 100.1% | 97.7% | 100.7% | 94.6% | 105.6% | 109.1% | 97.8% | 108.5% | 94.7% | 100.3% | 106.1% | 105.8% | 110.9% | 102.2% | 105.8% | 97.8% | 99.1% | 106.1% | 111.3% | 94.7% | 106.4% | 109.9% | 101.5% | 99.7% | 109.1% | 105.6% | 107.6% | 120.5% | 118.1% | 94.2% | 106.1% | 112.9% | 96.5% | 100.3% | 99.6% |
| 2020-09-01 | 104.1% | 104.9% | 97.7% | 113.9% | 99.4% | 103.5% | 112.4% | 100.6% | 109.7% | 116.8% | 111.3% | 101.7% | 97.2% | 119.3% | 94.0% | 103.7% | 98.9% | 100.5% | 98.4% | 101.2% | 95.3% | 105.5% | 109.7% | 97.5% | 107.8% | 95.5% | 100.2% | 106.5% | 105.8% | 111.7% | 102.5% | 102.2% | 103.3% | 99.1% | 106.6% | 111.4% | 95.2% | 106.9% | 110.5% | 101.7% | 100.3% | 109.5% | 106.0% | 108.5% | 121.3% | 118.8% | 93.9% | 106.0% | 112.8% | 96.7% | 100.7% | 99.6% |
| 2020-10-01 | 104.5% | 104.5% | 98.0% | 114.1% | 99.0% | 103.1% | 112.8% | 99.6% | 107.9% | 116.3% | 110.3% | 106.8% | 100.5% | 119.4% | 93.6% | 103.7% | 99.0% | 100.5% | 98.7% | 100.9% | 95.5% | 104.9% | 109.1% | 96.6% | 106.8% | 95.9% | 99.9% | 106.4% | 105.7% | 111.4% | 102.3% | 102.5% | 102.8% | 98.4% | 106.6% | 111.0% | 95.1% | 107.1% | 110.4% | 101.4% | 98.2% | 109.6% | 106.1% | 108.6% | 121.3% | 119.0% | 93.3% | 105.4% | 112.4% | 96.6% | 100.7% | 99.4% |
| 2020-11-01 | 104.3% | 104.1% | 98.5% | 114.3% | 98.8% | 103.2% | 113.4% | 99.4% | 108.6% | 115.7% | 110.4% | 106.6% | 102.0% | 119.8% | 93.6% | 103.8% | 99.3% | 100.6% | 99.0% | 100.8% | 96.0% | 104.8% | 109.1% | 96.3% | 106.0% | 96.2% | 99.8% | 106.4% | 105.7% | 111.5% | 102.2% | 103.3% | 102.4% | 98.3% | 107.0% | 110.7% | 95.2% | 107.3% | 110.5% | 101.3% | 98.8% | 109.7% | 106.2% | 108.8% | 121.7% | 119.3% | 93.1% | 105.1% | 112.3% | 96.6% | 100.8% | 99.2% |
| 2020-12-01 | 104.4% | 103.7% | 99.0% | 114.5% | 98.7% | 103.5% | 114.1% | 99.2% | 109.2% | 115.1% | 110.7% | 106.6% | 103.1% | 120.1% | 93.7% | 103.8% | 99.5% | 100.5% | 99.2% | 100.8% | 96.5% | 105.1% | 109.0% | 94.5% | 105.2% | 96.4% | 99.7% | 106.4% | 105.7% | 111.8% | 102.2% | 103.7% | 102.0% | 98.1% | 107.5% | 110.5% | 95.1% | 107.4% | 110.8% | 101.1% | 99.1% | 109.7% | 106.2% | 108.8% | 122.1% | 119.5% | 92.9% | 104.9% | 112.4% | 96.7% | 100.9% | 99.2% |
| 2021-01-01 | 104.1% | 103.3% | 99.2% | 114.6% | 98.5% | 103.5% | 114.3% | 98.9% | 109.6% | 114.2% | 110.6% | 106.4% | 103.1% | 120.3% | 93.6% | 103.6% | 99.6% | 100.3% | 99.3% | 100.6% | 96.8% | 104.7% | 108.6% | 95.7% | 104.4% | 96.4% | 99.6% | 106.4% | 105.7% | 111.8% | 102.0% | 104.0% | 101.4% | 97.9% | 107.6% | 110.2% | 95.0% | 107.5% | 110.8% | 101.0% | 99.1% | 109.7% | 106.2% | 108.7% | 122.1% | 119.7% | 92.8% | 104.7% | 112.4% | 96.8% | 101.0% | 99.1% |
| 2021-02-01 | 104.2% | 103.1% | 99.5% | 114.9% | 98.4% | 103.7% | 114.7% | 98.9% | 110.0% | 113.8% | 110.8% | 106.4% | 103.4% | 120.6% | 93.7% | 103.6% | 99.8% | 100.3% | 99.5% | 100.7% | 97.1% | 104.6% | 108.5% | 95.6% | 104.0% | 96.5% | 99.7% | 106.6% | 105.8% | 111.8% | 102.0% | 104.2% | 101.3% | 97.7% | 107.8% | 110.0% | 95.0% | 107.6% | 111.1% | 100.9% | 99.4% | 109.7% | 106.3% | 108.6% | 122.4% | 119.9% | 92.9% | 104.6% | 112.5% | 97.0% | 101.1% | 99.1% |
| 2021-03-01 | 104.4% | 103.1% | 99.8% | 115.2% | 98.5% | 104.2% | 115.1% | 98.9% | 110.5% | 114.0% | 111.2% | 106.5% | 103.7% | 120.8% | 93.8% | 103.7% | 100.1% | 100.4% | 99.7% | 100.9% | 97.4% | 104.8% | 108.6% | 95.6% | 103.8% | 96.6% | 99.8% | 107.0% | 106.0% | 111.7% | 102.1% | 104.3% | 101.3% | 99.8% | 108.1% | 110.0% | 95.1% | 107.7% | 111.4% | 100.8% | 99.7% | 109.9% | 106.5% | 108.7% | 122.6% | 120.2% | 93.0% | 104.7% | 112.7% | 97.2% | 101.3% | 99.1% |
| 2021-04-01 | 104.6% | 103.1% | 100.2% | 115.5% | 98.5% | 104.7% | 115.5% | 99.2% | 110.8% | 114.5% | 111.7% | 106.6% | 104.3% | 121.1% | 94.0% | 103.8% | 100.4% | 100.5% | 100.0% | 101.2% | 97.7% | 105.0% | 108.9% | 95.8% | 103.9% | 96.6% | 99.8% | 107.3% | 106.2% | 111.4% | 102.2% | 104.8% | 101.7% | 99.8% | 108.4% | 109.9% | 95.3% | 107.8% | 111.6% | 100.8% | 100.1% | 110.2% | 106.8% | 108.8% | 122.9% | 120.5% | 93.2% | 104.7% | 113.0% | 97.5% | 101.4% | 99.1% |
| 2021-05-01 | 104.5% | 103.1% | 100.3% | 115.7% | 98.5% | 104.9% | 115.7% | 99.2% | 111.0% | 115.1% | 112.2% | 106.7% | 104.6% | 121.3% | 94.1% | 103.8% | 100.6% | 100.6% | 100.2% | 101.3% | 97.7% | 105.2% | 108.9% | 96.0% | 104.0% | 96.5% | 99.8% | 107.7% | 106.3% | 111.0% | 102.2% | 104.7% | 101.8% | 99.5% | 108.7% | 109.7% | 95.5% | 107.8% | 111.6% | 100.7% | 100.3% | 110.4% | 107.0% | 109.0% | 123.1% | 120.8% | 93.3% | 104.6% | 113.2% | 97.7% | 101.5% | 99.0% |
| 2021-06-01 | 104.7% | 103.0% | 100.7% | 115.9% | 98.5% | 105.5% | 116.2% | 99.7% | 111.1% | 116.0% | 112.9% | 106.8% | 105.3% | 121.6% | 94.3% | 103.7% | 100.8% | 100.7% | 100.3% | 101.4% | 97.9% | 105.9% | 109.3% | 96.3% | 104.2% | 96.5% | 99.8% | 107.9% | 106.5% | 110.6% | 102.2% | 105.4% | 102.1% | 99.7% | 109.0% | 109.6% | 95.6% | 107.8% | 111.7% | 100.6% | 100.7% | 110.5% | 107.2% | 109.2% | 123.5% | 121.0% | 93.4% | 104.5% | 113.5% | 97.9% | 101.6% | 98.9% |
| 2021-07-01 | 104.8% | 102.8% | 100.8% | 116.0% | 98.4% | 105.5% | 116.2% | 99.6% | 111.0% | 116.4% | 113.2% | 106.8% | 105.4% | 121.8% | 94.3% | 103.4% | 100.8% | 100.7% | 100.5% | 101.1% | 97.6% | 106.0% | 109.2% | 96.4% | 104.2% | 96.3% | 99.8% | 108.1% | 106.6% | 110.1% | 102.1% | 104.9% | 102.0% | 99.2% | 109.3% | 109.6% | 95.6% | 107.6% | 111.5% | 100.3% | 100.7% | 110.6% | 107.3% | 109.3% | 123.6% | 121.2% | 93.3% | 104.4% | 113.8% | 97.9% | 101.5% | 98.8% |
| 2021-08-01 | 104.9% | 102.7% | 101.2% | 116.0% | 98.3% | 105.6% | 116.3% | 99.6% | 110.9% | 116.7% | 113.5% | 106.9% | 105.5% | 121.9% | 94.4% | 103.0% | 100.7% | 100.6% | 100.7% | 100.9% | 97.4% | 106.4% | 109.3% | 96.4% | 104.4% | 96.1% | 99.9% | 108.3% | 106.8% | 109.7% | 102.0% | 104.9% | 102.0% | 98.9% | 109.5% | 109.6% | 95.5% | 107.3% | 111.6% | 100.0% | 100.6% | 110.6% | 107.4% | 109.3% | 123.7% | 121.4% | 93.3% | 104.3% | 114.2% | 98.0% | 101.5% | 98.7% |
| 2021-09-01 | 104.9% | 102.6% | 101.4% | 116.0% | 98.3% | 105.4% | 116.1% | 99.5% | 110.7% | 116.5% | 113.5% | 106.9% | 105.2% | 122.0% | 94.4% | 102.7% | 100.5% | 100.5% | 100.9% | 100.7% | 97.1% | 106.2% | 109.2% | 96.4% | 104.5% | 95.9% | 99.9% | 108.4% | 107.0% | 109.5% | 101.9% | 104.3% | 101.7% | 98.3% | 109.7% | 109.7% | 95.4% | 107.2% | 111.6% | 99.8% | 100.3% | 110.6% | 107.4% | 109.4% | 123.8% | 121.6% | 93.3% | 104.3% | 114.5% | 98.0% | 101.4% | 98.7% |
| 2021-10-01 | 105.0% | 102.7% | 101.8% | 116.1% | 98.4% | 105.5% | 116.3% | 99.6% | 110.7% | 116.6% | 113.7% | 107.1% | 105.2% | 122.1% | 94.6% | 102.6% | 100.4% | 100.5% | 101.0% | 100.8% | 97.0% | 106.5% | 109.3% | 96.4% | 104.6% | 95.9% | 100.1% | 108.6% | 107.2% | 109.5% | 101.9% | 104.1% | 101.8% | 98.1% | 109.8% | 109.9% | 95.4% | 107.1% | 111.9% | 99.6% | 100.1% | 110.7% | 107.5% | 109.5% | 124.0% | 121.8% | 93.3% | 104.4% | 114.7% | 98.1% | 101.4% | 98.7% |
| 2021-11-01 | 105.3% | 102.7% | 101.9% | 116.1% | 98.4% | 105.2% | 116.3% | 99.4% | 110.7% | 116.3% | 113.6% | 107.1% | 105.0% | 122.1% | 94.6% | 102.6% | 100.3% | 100.4% | 101.1% | 100.9% | 96.8% | 106.2% | 109.1% | 96.3% | 104.6% | 95.9% | 100.1% | 108.7% | 107.2% | 109.5% | 102.0% | 103.8% | 101.7% | 97.9% | 109.8% | 110.0% | 95.4% | 107.2% | 111.9% | 99.6% | 99.9% | 110.7% | 107.5% | 109.5% | 123.9% | 121.8% | 93.3% | 104.4% | 114.7% | 98.1% | 101.4% | 98.7% |
| 2021-12-01 | 105.4% | 102.7% | 101.9% | 116.1% | 98.3% | 105.1% | 116.3% | 99.2% | 110.8% | 116.3% | 113.6% | 107.0% | 105.1% | 122.1% | 94.5% | 102.7% | 100.3% | 100.4% | 101.1% | 101.0% | 96.7% | 106.1% | 109.0% | 96.3% | 104.6% | 96.0% | 100.0% | 108.7% | 107.2% | 109.6% | 102.0% | 103.8% | 101.5% | 97.9% | 109.7% | 109.9% | 95.4% | 107.2% | 111.9% | 99.6% | 99.8% | 110.7% | 107.5% | 109.5% | 123.9% | 121.8% | 93.3% | 104.4% | 114.6% | 98.1% | 101.4% | 98.7% |
| 2022-01-01 | 106.3% | 103.1% | 102.5% | 116.3% | 98.6% | 105.6% | 116.9% | 100.0% | 111.1% | 116.6% | 114.1% | 107.4% | 105.3% | 122.5% | 95.1% | 102.7% | 100.6% | 100.5% | 101.3% | 101.3% | 96.9% | 106.4% | 109.5% | 96.5% | 105.1% | 96.1% | 100.3% | 108.9% | 107.3% | 109.7% | 102.1% | 104.0% | 101.9% | 98.1% | 110.0% | 110.4% | 95.5% | 107.3% | 112.6% | 99.7% | 99.7% | 110.8% | 107.7% | 109.7% | 124.3% | 121.9% | 93.6% | 104.8% | 115.1% | 98.3% | 101.4% | 98.8% |
| 2022-02-01 | 106.5% | 103.5% | 102.7% | 116.5% | 99.0% | 105.7% | 117.4% | 100.1% | 111.1% | 116.4% | 114.3% | 107.8% | 105.2% | 122.9% | 95.5% | 103.1% | 101.0% | 100.5% | 101.4% | 101.7% | 97.0% | 106.3% | 109.6% | 96.6% | 105.6% | 96.4% | 100.5% | 109.1% | 107.4% | 110.0% | 102.2% | 103.6% | 102.2% | 97.9% | 110.2% | 110.8% | 95.6% | 107.4% | 113.0% | 99.7% | 99.6% | 111.0% | 107.8% | 110.1% | 124.7% | 122.1% | 93.7% | 105.2% | 115.7% | 98.3% | 101.5% | 98.9% |
| 2022-03-01 | 106.8% | 104.0% | 102.7% | 116.7% | 99.3% | 106.1% | 117.8% | 100.6% | 111.2% | 116.6% | 114.8% | 108.1% | 105.2% | 123.5% | 95.9% | 103.6% | 101.3% | 100.7% | 101.6% | 102.3% | 96.9% | 106.5% | 109.7% | 96.9% | 106.0% | 96.7% | 100.7% | 109.6% | 107.6% | 110.4% | 102.5% | 103.5% | 102.3% | 98.0% | 110.5% | 110.9% | 95.8% | 107.9% | 113.4% | 100.0% | 99.7% | 111.3% | 108.1% | 110.5% | 125.0% | 122.8% | 94.1% | 105.6% | 116.3% | 98.4% | 101.7% | 98.9% |
| 2022-04-01 | 106.6% | 104.3% | 102.7% | 116.9% | 99.7% | 106.6% | 118.3% | 101.1% | 111.2% | 116.7% | 115.1% | 108.5% | 105.4% | 124.2% | 96.2% | 104.1% | 101.7% | 100.9% | 101.7% | 102.8% | 96.8% | 106.4% | 109.7% | 97.2% | 106.3% | 97.0% | 100.9% | 110.0% | 107.8% | 110.8% | 102.7% | 103.8% | 102.4% | 98.3% | 111.1% | 111.2% | 96.0% | 108.3% | 114.0% | 100.3% | 99.7% | 111.7% | 108.4% | 111.1% | 125.4% | 123.4% | 94.5% | 106.1% | 116.9% | 98.4% | 101.8% | 99.0% |
| 2022-05-01 | 106.8% | 104.6% | 102.9% | 117.4% | 99.9% | 107.0% | 118.9% | 101.5% | 111.5% | 116.9% | 115.7% | 108.7% | 105.7% | 125.0% | 96.4% | 104.6% | 102.0% | 101.1% | 101.8% | 103.2% | 96.9% | 106.6% | 109.7% | 97.6% | 106.6% | 97.3% | 100.7% | 110.4% | 108.0% | 111.3% | 103.0% | 104.1% | 102.7% | 98.8% | 111.8% | 111.2% | 96.3% | 108.7% | 114.4% | 100.8% | 99.9% | 112.1% | 108.8% | 111.7% | 125.9% | 124.0% | 94.7% | 106.5% | 117.3% | 98.6% | 101.8% | 99.0% |
| 2022-06-01 | 106.6% | 104.8% | 103.0% | 117.6% | 100.1% | 107.3% | 119.2% | 101.8% | 111.6% | 116.9% | 116.1% | 108.9% | 105.9% | 125.7% | 96.4% | 105.0% | 102.3% | 101.2% | 101.8% | 103.2% | 97.0% | 107.0% | 109.7% | 97.7% | 106.7% | 97.3% | 100.3% | 110.8% | 108.1% | 111.6% | 103.3% | 104.5% | 102.8% | 99.2% | 112.1% | 111.1% | 96.3% | 108.8% | 114.6% | 100.9% | 100.2% | 112.2% | 109.2% | 111.9% | 126.2% | 124.4% | 95.1% | 106.7% | 117.4% | 98.7% | 101.7% | 99.0% |
| 2022-07-01 | 106.5% | 105.0% | 102.8% | 117.8% | 100.2% | 107.2% | 119.2% | 101.7% | 111.6% | 116.7% | 116.4% | 108.8% | 105.9% | 126.2% | 96.3% | 105.5% | 102.4% | 101.1% | 101.7% | 103.0% | 96.8% | 107.0% | 109.4% | 97.8% | 106.6% | 97.3% | 99.7% | 111.0% | 108.0% | 111.7% | 103.6% | 104.5% | 102.3% | 99.4% | 112.4% | 110.9% | 96.3% | 109.0% | 114.6% | 100.9% | 100.5% | 112.0% | 109.4% | 111.8% | 126.5% | 124.7% | 95.3% | 106.7% | 117.1% | 98.8% | 101.4% | 98.8% |
| 2022-08-01 | 107.0% | 105.1% | 102.8% | 118.2% | 100.1% | 107.3% | 119.5% | 102.0% | 111.6% | 116.5% | 116.9% | 108.7% | 106.2% | 126.8% | 96.3% | 105.7% | 102.4% | 100.8% | 101.7% | 102.6% | 96.6% | 107.4% | 109.4% | 97.7% | 106.4% | 97.1% | 99.6% | 111.3% | 108.0% | 112.2% | 103.9% | 105.2% | 102.1% | 99.7% | 112.6% | 110.7% | 96.2% | 109.1% | 114.7% | 100.9% | 100.8% | 111.8% | 109.4% | 111.5% | 126.6% | 124.9% | 95.5% | 106.5% | 116.8% | 98.7% | 101.1% | 98.6% |
| 2022-09-01 | 107.0% | 105.1% | 102.4% | 118.6% | 100.0% | 106.9% | 119.4% | 101.9% | 111.5% | 115.6% | 117.0% | 108.6% | 105.9% | 127.2% | 96.1% | 105.7% | 102.4% | 100.7% | 101.6% | 102.3% | 96.4% | 106.9% | 109.0% | 97.8% | 106.3% | 96.9% | 99.6% | 111.4% | 108.1% | 112.9% | 104.1% | 104.8% | 101.8% | 99.3% | 112.7% | 110.3% | 96.0% | 109.0% | 114.4% | 100.9% | 101.1% | 111.6% | 109.4% | 111.0% | 126.5% | 125.1% | 95.6% | 106.5% | 116.6% | 98.6% | 100.7% | 98.5% |
| 2022-10-01 | 107.0% | 104.6% | 101.1% | 119.7% | 101.3% | 106.9% | 117.2% | 102.5% | 110.4% | 117.3% | 118.4% | 107.7% | 106.4% | 126.5% | 96.3% | 106.0% | 103.0% | 101.1% | 100.6% | 101.9% | 95.7% | 105.4% | 108.4% | 97.2% | 106.5% | 95.3% | 100.1% | 111.8% | 107.7% | 115.2% | 103.9% | 106.8% | 101.7% | 100.5% | 113.4% | 112.0% | 95.0% | 109.5% | 113.5% | 101.4% | 99.4% | 110.7% | 108.6% | 108.9% | 127.6% | 126.2% | 97.4% | 109.2% | 116.7% | 97.1% | 99.2% | 100.0% |
| 2022-11-01 | 106.9% | 104.6% | 101.2% | 119.7% | 101.4% | 106.9% | 117.3% | 102.4% | 110.4% | 117.4% | 118.4% | 107.8% | 106.4% | 126.5% | 96.4% | 106.0% | 103.1% | 101.1% | 100.5% | 102.0% | 95.8% | 105.4% | 108.3% | 97.2% | 106.5% | 95.3% | 100.1% | 111.7% | 107.7% | 115.2% | 103.9% | 106.7% | 101.8% | 100.5% | 113.4% | 112.1% | 95.0% | 109.5% | 113.5% | 101.4% | 99.3% | 110.7% | 108.7% | 108.9% | 127.6% | 126.2% | 97.6% | 109.4% | 116.7% | 97.1% | 99.2% | 100.0% |
| 2022-12-01 | 107.2% | 104.6% | 101.2% | 119.7% | 101.4% | 106.9% | 117.3% | 102.5% | 110.5% | 117.5% | 118.3% | 107.8% | 106.4% | 126.5% | 96.5% | 106.0% | 103.2% | 101.2% | 100.6% | 102.0% | 95.8% | 105.3% | 108.3% | 97.2% | 106.5% | 95.3% | 100.1% | 111.7% | 107.7% | 115.2% | 103.9% | 106.8% | 101.9% | 100.6% | 113.4% | 112.2% | 95.1% | 109.5% | 113.5% | 101.4% | 99.2% | 110.7% | 108.7% | 108.9% | 127.5% | 126.2% | 97.7% | 109.5% | 116.7% | 97.2% | 99.2% | 100.0% |
| 2023-01-01 | 107.7% | 104.7% | 101.4% | 119.9% | 101.5% | 107.1% | 117.6% | 102.4% | 110.6% | 117.8% | 118.5% | 107.9% | 106.3% | 126.7% | 96.5% | 106.0% | 103.1% | 101.3% | 100.6% | 102.3% | 96.0% | 105.3% | 108.4% | 97.3% | 106.5% | 95.3% | 100.1% | 111.9% | 107.7% | 115.3% | 104.1% | 107.1% | 102.2% | 100.7% | 113.5% | 112.3% | 95.1% | 109.7% | 113.5% | 101.6% | 99.2% | 110.9% | 108.7% | 108.9% | 128.0% | 126.6% | 97.9% | 110.0% | 116.9% | 97.1% | 99.2% | 100.3% |
| 2023-02-01 | 108.0% | 104.7% | 101.5% | 120.1% | 101.5% | 107.2% | 118.0% | 102.3% | 110.6% | 117.9% | 118.8% | 108.1% | 106.2% | 127.0% | 96.6% | 106.0% | 103.1% | 101.5% | 100.6% | 102.7% | 96.1% | 105.4% | 108.7% | 97.4% | 106.4% | 95.3% | 100.3% | 112.0% | 107.7% | 115.4% | 104.0% | 107.5% | 102.5% | 100.8% | 113.6% | 112.4% | 95.4% | 109.9% | 113.4% | 101.7% | 99.2% | 111.2% | 108.9% | 109.1% | 128.5% | 127.1% | 98.1% | 110.4% | 117.3% | 97.0% | 99.3% | 100.6% |
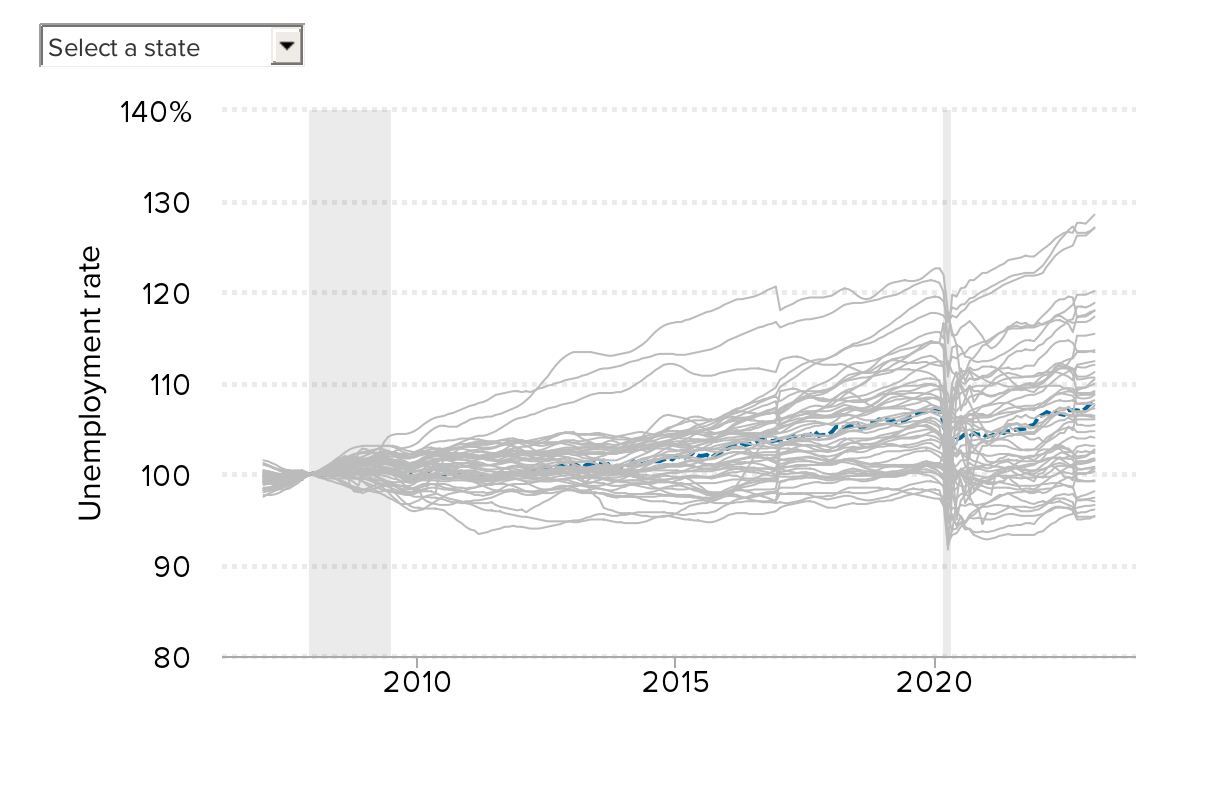
Notes: Shaded areas represent recessions.
Source: EPI/EARN analysis of Bureau of Labor Statistics Local Area Unemployment data.
When workers lose a job or cannot find work, they and their families lose wages and benefits, and the adverse effects may last a very long time as career trajectories are interrupted. When more workers are unemployed, it also depresses wage growth for those workers who have a job, since employers have little need to raise pay to attract or retain staff. Although the country remains on a positive trend of job growth and falling unemployment, many states still have rates of job growth that are leaving many unable to find work and paychecks failing behind. To ensure workers in every community have access to jobs and rising pay, policymakers should prioritize a full employment agenda.
Data come from the State and Regional Employment report, released monthly by the Bureau of Labor Statistics. Explore the map to see how these indicators differ across the country and read EPI’s recent research analyzing jobs and unemployment.