Briefing Paper #158
by Joydeep Roy and Lawrence Mishel
In late summer of 2004 researchers at the American Federation of Teachers (AFT), drawing upon data in a not-yet-published study of charter schools by the National Assessment of Educational Progress (NAEP), issued a report concluding that charter school students had lower achievement in both reading and mathematics compared to students in regular public schools. The differences were significant overall as well as for some of the very groups of students for whom charter schools are said by proponents to offer particular benefits, e.g., low-income children eligible for free or reduced-price lunches and students in central cities. However, the AFT also found that minorities in charter schools had test scores that were not significantly different than those of their counterparts in regular public schools.1
The AFT study, reported on the front page of the New York Times (Schemo 2004), generated a spirited debate among researchers and policy analysts in the education community and beyond. In an important rebuttal, Professor Caroline Hoxby of Harvard University argued that the AFT report was fundamentally flawed because of its reliance on the NAEP’s small and uneven sample size (Hoxby 2004a).2 In her own study, Hoxby compared reading and math scores of fourth-grade students in nearly all (99%) charter schools to the scores of fourth-grade students in neighboring regular public schools. (She selected fourth grade for consistency with the NAEP sample.)3 For the country as a whole, Hoxby found that charter school students were 3.8% more likely to be proficient on their state’s reading exam when compared to students in the nearest regular public school; the advantage rose to 4.9% when the racial composition of the charter school and the nearest regular public school was similar. The corresponding charter advantages in math were 1.6% and 2.8%. North Carolina was the only state in which charter students’ proficiency was lower in a statistically significant way.4
Hoxby’s analysis, however, suffers from the fact that her method of comparing charter schools to their neighboring regular public schools (and to those neighboring public schools with a similar racial composition) inadequately controls for student backgrounds. In her sample of matched schools there are often significant differences in the demographic and socioeconomic characteristics of the students. For instance, comparing the charter schools in Hoxby’s sample to the matched neighboring public schools with a similar racial composition shows that the charter schools have a disproportionately higher black population (34% vs. 28%) and higher white population (43% vs. 36%), while the share of Hispanics is lower (18% vs. 30%). Her sample of charter schools also has disproportionately fewer low-income students than does the matched “racially similar” sample of neighboring public schools (49% vs. 60%). The same picture emerges in terms of the demographics of charter schools in central cities: charter schools serve a disproportionately lower share of minorities and low-income students compared to their matched regular public schools. Thus, without further controls, Hoxby’s method of comparing “racially matched” schools does not appear to be effective in controlling for student characteristics.5
Hoxby’s result of a positive charter effect on math proficiency disappears when racial composition is controlled for directly. Further, when both racial composition and low-income status are controlled for, the positive effect of attending a charter school disappears for both math and reading (it becomes very small and not statistically significantly different than zero). Thus, Hoxby’s conclusion that “although it is too early to draw sweeping conclusions, the initial indications are that the average student attending a charter school has higher achievement than he or she otherwise would” (Hoxby 2004a) does not hold up against direct controls for student background.6
Though Hoxby’s sample includes charter schools from 37 states, only nine states have close to or more than 50 charter schools. These nine states are considered “major charter states” — the performance of charter schools in these states is of particular interest to policy makers. The states are California (200 schools), Michigan (133), Florida (98), Arizona (96), Texas (90), Ohio (67), North Carolina (65), Colorado (64), and Pennsylvania (48).
Controlling for racial composition, California alone among the major charter states retains a significant charter advantage in reading proficiency. For math, charter schools in none of the nine states have any statistically significant edge over their matched regular public schools. Controlling for low-income status (proxied by free and reduced-price lunch eligibility) in addition to racial composition, only one state (California) has a significant charter school advantage in reading and none in math. In fact, in the four states where charter school students are relatively similar in socioeconomic composition to their peers in matched regular public schools7 — Michigan, North Carolina, Ohio, and Texas — the effect of charter schools is mostly negative in both reading and math, though the difference is rarely statistically significant.
In terms of solely central city schools, charters have no significant effect in math once racial composition is controlled for; further controlling for low-income status lowers the charter school coefficient. There is a modest and marginally significant positive effect in reading when only racial composition is controlled for, but this advantage vanishes when a control is added for low-income status. In fact, analyses by location show no significant positive impact in either math or reading for charter schools in any type of location: central city, suburb, town, or rural area.
The selective nature of charter schools (students choose to attend charter schools; they are not assigned randomly) may be one reason why some of the smaller states in terms of charter presence enjoy a large charter advantage in Hoxby’s results. For example, in Louisiana charter schools outperform their matched regular public schools by 30 points in both reading and mathematics. Yet Louisiana’s charter schools are majority white, while the share of whites in the matched public schools is only 12%; there is also a large 40 percentage-point difference in the share of students eligible for free or reduced-price lunches. The case of Nevada is similar: the proportion of whites in charter schools and matched regular public schools is 55% and 26%, respectively, and there is a 30 percentage-point difference in the shares eligible for lunch subsidies.8
During the recent controversy generated by the release of the NAEP charter school pilot study results, many education analysts correctly noted that it is problematic to discern the true effect of charter schools on achievement using cross-sectional or “point-in-time” data. Indeed, the most persuasive and informative assessments of charter school performance are based on analyses of longitudinal data (following schools or students over time) that can control for observed and unobserved characteristics of students and schools, especially initial test scores. Nevertheless, cross-sectional analysis has frequently been employed to learn about factors driving educational achievement, including charter schools effects,9 but they are more persuasive when they control for student and school characteristics. The cross-sectional analyses offered by Hoxby have been widely cited by charter school advocates, including former Secretary of Education Rod Paige. The purpose of this reanalysis is to assess whether Hoxby’s cross-sect
ional matched schools study is useful or informative regarding the impact of charter schools on achievement.
The following section outlines the dataset used by Hoxby and discusses how we incorporate data on student characteristics in the charter and matched schools. This is followed by a comparison of the demographic composition of students attending charter schools and students attending the matched regular public schools. The subsequent section then re-estimates the charter school advantage by state and type of locale by explicitly accounting for differences in racial composition and low-income status across charters and matched public schools. Appendix A describes our methodology for measuring the charter school effect, and Appendix B re-examines the Hoxby results under alternative weighting schemes and fixed effects estimation.
Hoxby’s dataset and its shortcomings
Professor Hoxby’s dataset10 consists of two separate samples, which differ only by the comparison group. In the first sample, henceforth called the distance sample, Hoxby matches the charter schools with their nearest regular public school.11 In the second sample, henceforth called the race sample, she matches charter schools with the nearest regular public school with a similar racial composition. Each sample has data on the names, locations, and achievement of the charter schools and their matched regular public schools. But the data do not include any other characteristics of the student body, including race and free or reduced-price lunch eligibility.
To incorporate information on such student characteristics, we assigned the schools their respective NCES unique identifying numbers and then merged this dataset with the Common Core of Data (CCD) Public Elementary/Secondary School Universe Survey Data for 2002-03. The CCD dataset has detailed information on every school, including enrollment, free lunch eligibility, and racial composition. Our merged dataset thus has information on the proficiency of the school’s students as well as their backgrounds.12
For a significant number of schools, both charter and regular public, the number of students receiving free or reduced-price lunches is missing from their data. Moreover, a number of schools show zero as their free-lunch-eligible population; on closer inspection, it turns out that a disproportionately larger number of these are charter schools. For example, in the distance sample, out of the 196 schools with zero as their free-lunch-eligibility number, 180 are charter schools. To avoid the problem of this disproportionate share biasing the results, which they might if they are mistakenly attributed, we have deleted these observations from any analyses using the free-lunch-eligibility variable.13 That is, when we include the percentage of free-lunch-eligible students in a school as an explanatory variable, we drop the observations that have either a missing value or zero as the reported free lunch number. The use of this smaller sample does not seem to impart a bias to an analysis of the charter school effect: replication of Hoxby’s analysis (shown below in Tables 3A and 3B) using these smaller samples yields estimates of charter advantage similar to those in her original study.
Of the 37 states in the sample, some have only a small number of charter schools. All schools (with relevant data) have been included in the calculation of the charter advantage at the national level. But when we consider individual states, we have restricted our analysis, as did Hoxby, to states that have close to or more than 200 charter school students in the relevant grade (Hoxby 2004a, Table 1). Some of these states have only a few charter schools in the sample — Delaware (8 schools), Idaho (9), Illinois (9), Louisiana (7), New Mexico (4), Nevada (5) and Oregon (8) — so their results should be treated with caution. We do not report the results with controls for these states, since the degrees of freedom are too low. Overall, the charter school effect is estimated separately for 25 individual states, and for 17 of these we report results that control for racial composition and low-income status.14
Data for schools in two states present particular problems. Hoxby’s initial results for Washington D.C. were mistakenly based on faulty statistics (see Dobbs 2004; Hoxby has since corrected the dataset, and her new (2004b) is based on updated proficiency data). So, when reporting the proficiency results for the individual states we do not include Washington D.C. When reporting the results for the nation as a whole we present two sets of results, one including and one excluding D.C.15
For North Carolina, Hoxby used a measure of proficiency known as the “performance composite” in the state. This measure summarizes the performance of students in a school with respect to attaining a particular achievement level, taking different grades and subjects into consideration. It is neither the fourth-grade reading score nor the fourth-grade math score, but rather a hybrid.16 For comparability, all of the analyses presented below use the same test information employed by Hoxby.17
With regard to comparison schools, Hoxby argues that the nearest public school, either in distance or in racial composition, should serve as an adequate control group for a charter school. However, charter schools are schools of choice, and it is possible that charter schools draw their students from multiple schools. This is especially true in cities, where charter schools are primarily located, and where a distance of two or three miles vs. one mile may not be much of a deterrent to attendance.18 In this study we take Hoxby’s matches as given, and investigate only whether controlling for student characteristics alters her results. In later work we will examine the selection criteria for comparison to regular public schools; it would be particularly interesting to see if associating a charter school with multiple regular public schools in the neighborhood, instead of a single one, generates different results.
With regard to proficiency measures, Hoxby uses the proportion of students in the fourth grade that scores above the state-mandated achievement level for proficiency. While this approach is undoubtedly useful, it should ideally be combined with other measures that look more closely at performance at the top or at the bottom (e.g., the percentage of students scoring at or above the basic and advanced levels). It is interesting to note that the NAEP data offer several measures of proficiency as well as scale test scores at the individual level that could provide a more robust measure of achievement.
The demographic composition of charter schools and Hoxby’s matched regular public schools
When comparing achievement between schools, it is important to account for differences in student characteristics. Here we focus on racial composition and free or reduced-price lunch eligibility; the latter characteristic is highly correlated with family socioeconomic status.19Table 1 shows that, for the nation as a whole, charter schools serve a higher proportion of blacks but fewer Hispanics than do regular public schools, and they serve a higher proportion of whites.20 Charter schools also serve a disproportionately lower percentage of free-lunch-eligible students than do their regular counterparts, 49% vs. 64% (note that the schools, nearly all charter, reporting zero free lunch eligibility are excluded from this comparison).21 Overall, it seems reasonable to conclude that charter schools serve a relatively more advantaged student body than do their matched regular public schools.22

The analysis by states in Table 1 includes all states with more than 10 charter schools, plus Louisiana and Nevada; the latter have fewer than 10 charter schools but are included because the
Hoxby study found a significant charter school advantage there. The two states with the largest number of charter schools, and the only two with more than 100 charter schools each, are California (200 schools) and Michigan (132). In Michigan the differences between charter schools and regular public schools appear to be small, though the former serve a somewhat higher proportion of blacks and a lower proportion of poor students. In California, however, charter schools serve a disproportionately lower percentage of Hispanics than do their matched schools and a higher percentage of whites. The share eligible for subsidized lunches is 21 percentage points lower in charter schools.
Three other states with close to 100 charter schools each are Arizona (95 schools), Florida (98) and Texas (90). Arizona, which leads the nation in the proportion of public school students attending charter schools (other than Washington D.C.), has a much lower proportion of Hispanics (26% vs. 46%) and a much higher proportion of whites (61% vs. 42%) in charter schools.23 The free lunch eligibility number is higher for charters, but less than 20% of the charter schools reported non-zero numbers. In Florida, charter schools seem to serve a higher proportion of whites, and there is a particularly large difference in terms of children qualifying for free lunch programs (37% in charter schools but 61% in matched regular public schools). In Texas, charter schools attract a much larger share of blacks and a correspondingly smaller share of Hispanics, though the differential in terms of low-income status is not large.
Some of the other states with a significant number of charter schools are Colorado (64 schools), North Carolina (65), Ohio (62) and Pennsylvania (48). In Colorado, as in most other states, charters serve a lower proportion of Hispanics, 15% vs. 27%, and a higher proportion of whites, 75% vs. 64%. They also have less than half as many free-lunch-eligible students as do regular public schools, 16% vs. 37%. In North Carolina and Ohio there is not much difference in the composition of the student bodies between charter and regular public schools.24 In Pennsylvania, however, charter schools serve a much larger proportion of whites and have a disproportionately lower share of free lunch students.
Among the states with a relatively small charter school movement, Louisiana and Nevada stand out for large differences between charter schools and their matched counterparts. In Louisiana, the proportion of blacks in charter schools is half that in regular public schools, and the charter schools are majority white despite being close to predominantly black (87%) regular public schools. Not surprisingly, the proportion of poor students is quite different across the two types of schools. In Nevada, the differences are not as stark but still significant. These differences can be important because in the Hoxby study charter schools have large proficiency advantages in both Louisiana (a 33-point gap in reading, 29 in mathematics) and Nevada (a 10-point gap in reading).25
This analysis shows that race and incomes of students in charter schools often differ systematically from those of students in matched regular public schools. Since these background attributes are believed to be correlated with academic performance, Hoxby’s methodology may not yield the true effect of attending a charter school. Whether better controls for student characteristics change the estimated advantage of charter schools is examined in the next section.
Tables 2A and 2B further compare the demographic composition of charter schools and regular public schools by looking specifically at location. The CCD survey classifies each school in 2002-03 as falling into one of eight different locales. Locales 1 and 2 refer to central city schools of large and mid-size cities, respectively. Locales 3 and 4 refer to the respective urban fringes. Locales 5 and 6 designate large and small towns, respectively. Locale 7 refers to a rural area outside the core-based statistical area (CBSA), while Locale 8 refers to a rural area inside a CBSA. For ease of comparison we have combined into single groups Locales 1 and 2 (central city), Locales 3 and 4 (urban fringe), Locales 5 and 6 (large/small town), and Locales 7 and 8 (rural).


Table 2A shows that the comparisons for the four separate locations26 follow the basic trends reported in Table 1. Charter schools located in central cities serve a higher proportion of blacks (48% vs. 37%) but a lower proportion of Hispanics (21% vs. 35%); on the whole, central city charter schools serve more whites (27% vs. 23%). Charter schools outside of central cities also disproportionately enroll blacks, but not to the degree that central city charter schools do. At the same time, however, charter schools outside of central cities are disproportionately white to a greater degree than their counterparts in central cities. Charter schools serve a lower proportion of Hispanics than do regular public schools in every location, though the differences are not large for large/small towns. Looking at all non-Asian minorities combined (Indians, Hispanics, and blacks), charter schools in all locations, including charter schools located in central cities, have a smaller proportion than do their matched regular public schools. As was seen in Table 1, charter schools serve a lower proportion of poor students as proxied by free or reduced-price lunch eligibility — there is a 13-17 point difference across the various locations.
Table 2B provides a closer look at the demographic composition of central city charter schools and regular public schools across major charter states.27 As we have seen above, for the U.S. as a whole, charter schools located in central cities serve a higher proportion of blacks (48% vs. 37%), but a smaller proportion of Hispanics (21% vs. 35%);28 there is also a significant 13 percentage-point difference in the percentage of students eligible for free or reduced-price lunches.29 In Arizona, California, Colorado, and Florida, charter schools in central cities serve a much smaller fraction of non-Asian minorities relative to the matched regular public schools. The largest gaps are in Colorado (where charter schools have a student population that is 63% white vs. the 40% share in matched regular public schools) and in Florida (52% white in charter schools, 38% in matched regular public schools). The differences in the composition of students are small for the other four states, Michigan, North Carolina, Ohio, and Texas. But in every state, charter schools have a smaller percentage of Hispanic students than do the regular public schools.30 Central city charter schools have a much lower proportion of poor students in nearly every state — Michigan and Texas are the exceptions, but even there the difference is at least 5 percentage points. (Central city charter schools in North Carolina seem to serve more poor students than the matched regular public schools, but data are available only for a handful of schools.)
Estimating the charter ‘advantage’
As we saw in the previous section, there are important differences in the demographic composition between the charter schools in Hoxby’s sample and the regular public schools that are matched to them. In this section we examine differences in reading and math proficiency between charter schools and these regular public school pairs, with and without controlling for student backgrounds. The methodology employed in this exercise is detailed in Appendix A.
Results for reading
Table 3A details the results for reading proficiency.31 The first column reproduces Hoxby’s estimates; state
s for which results were not statistically significant are indicated by “n/r” (“not reporting”).32 The second column follows Hoxby’s specification and replicate her results. The next two columns report results controlling for two demographic characteristics, the racial composition of the schools (column 3) and the extent of poverty (column 4), as measured by the percentage of students eligible for free or reduced-price lunch programs. For ease of comparison, (as in Hoxby), all the regressions in the table have been weighted by the number of test takers in the respective charter schools. Since in some states there are a significant number of schools with missing free-lunch data, the sample size sometimes drops sharply as we go from the third to the fourth columns. The last column reports the results of Hoxby’s specification run on this smaller sample.

For the nation as a whole, Hoxby’s estimates show charter schools to have a statistically significant 4.9-point advantage in reading proficiency.33 However, when the racial composition and low-income status at the matched schools are taken into account, the charter school advantage drops sharply. Race alone reduces the charter advantage at the national level to less than a third (from 4.80 to 1.47); the further inclusion of free lunch eligibility drops it to a statistically insignificant 1.10.34
As with the national results, the findings of a charter school advantage in most states disappear once direct controls are added for student race and income. In California, the charter school advantage drops by more than half when controlling either for race or for race and poverty, then increases slightly when further controlling for income (note though that data on free lunch eligibility are missing for a large percentage of California charter schools). In three other big states — Arizona, Florida, and Texas — controlling for race and poverty measures yields a negative charter school effect, though the results are generally not significant. In Michigan, the only other state with more than 100 charter schools in the sample, allowing for race and poverty increases the estimated advantage of the charter schools, but it still remains negative. The charter school advantage also drops in major charter states like Colorado (declining from a statistically significant 11-point advantage to a statistically insignificant 1 point ) and Pennsylvania (from 8.5 points to less than 1 point). Hawaii, which is not a big charter school state, nevertheless witnesses a huge drop in the charter advantage when controlling for student characteristics.
These differences when race and income are controlled for would seem to suggest that much of the estimated charter school advantage in the Hoxby study reflects the fact that charters tend to enroll students from higher-scoring racial and income groups than do their nearest regular public schools. If we hold racial composition and low-income status constant — in effect, comparing charter schools and regular public schools with identical racial composition and income levels — the charter school advantage in the U.S. overall and in most states disappears, becoming substantially smaller, sometimes negative, and statistically insignificant.
On the other hand, the charter advantage remains important and significant in some states even after controlling for race and poverty. In Georgia, charter schools seem to maintain a statistically significant 5-point advantage; in Wisconsin they do even better. In New Jersey and Massachusetts, too, charter schools appear to have an edge, though the differences are not statistically significant.
Overall, one can conclude that controlling for race and poverty significantly reduces charter schools’ proficiency advantage, both at the national level and for individual states. Of the major charter states, only California manages to have a significant charter school advantage after controlling for student characteristics.
Results for mathematics
Table 3B shows the results for proficiency in mathematics. Hoxby’s estimates imply that, for the nation as a whole, about 3 percentage points more students in charter schools are proficient in math, compared to their matched regular public schools. However, the 3-point advantage drops sharply when race and income are taken into account — to 0.23, when only racial composition is controlled for, and to 0.33, when both racial composition and low-income status are controlled for. (The coefficient becomes negative if D.C. is omitted, though it is statistically insignificantly different from zero.)

The charter school advantage for math is lower than that for reading at the national level and tends to be lower at the state level as well. Of the nine major charter states (California, Michigan, Florida, Arizona, Texas, North Carolina, Colorado, Ohio, and Pennsylvania), none has a charter school proficiency advantage that is statistically significant once race and poverty are controlled for. In fact, only two out of the nine — Colorado (2.45) and California (0.04) — show a positive (though insignificant) charter coefficient when controlling just for race. The only positive and significant effects are found in Wisconsin and New Jersey. Tables A-3A and A-3B show the results for the distance sample, where the charter schools are matched with their nearest regular public schools. The coefficients are very similar to those in Tables 3A and 3B, respectively, though overall they are slightly smaller in magnitude.
Results for different locales
It is often argued that charter schools serve a disproportionate number of central and inner-city children, and that they are particularly effective in helping these overwhelmingly poor and minority students. Indeed, CCD survey data confirm that charter schools are more likely to serve urban populations. Most are located either in large cities (35%) and their urban fringes (25%), or in mid-size cities (17%) and their urban fringes (8%). Only about 3% of all charter schools are in large or small towns, and about 12% are in rural areas. (Appendix Table A-4 shows the distribution of charter schools by locales; the exact definitions are available on the CCD website at http://nces.ed.gov/ccd/data/txt/psu021alay.txt.)
Table 4 shows the estimates of charter school advantage for both reading and math across different locales (the CCD’s eight locales are combined here into four groups, as in Tables 2A and 2B). The first column under each subject lists the original (aggregate) Hoxby estimates, and the second column applies Hoxby’s methodology to produce estimates of the charter school advantage for the different locations. The third column controls for racial composition, and the fourth column for poverty in addition to race. All the results are weighted by the number of test takers in the respective charter schools, as in Hoxby, to maintain comparability of the results.

With no other controls, charter schools seem to enjoy an advantage over public schools in reading regardless of location. The effect in the urban fringe is the largest, exceeding the (aggregate) effect for the nation as a whole. The advantage for central cities becomes much smaller when Washington D.C. is taken out, but it is still significant. But the addition of controls for race and income reduces the charter school advantage in all locales to the point where the effect is no longer statistically significant. In particular, there is now no longer any meaningful charter
school advantage in either the central cities or their urban fringes.
The results for mathematics are similar. Under Hoxby’s methodology, i.e., with no other controls, there is a small charter school advantage in the urban fringes (and a marginally significant effect for central cities, though this appears to be due mostly to Washington D.C.). But there is no charter school advantage in math in any locale once the analysis introduces a direct control for student racial composition and/or poverty.35
The results for the distance sample, shown in Appendix Table A-5, are similar. Initially, charter schools seem to hold a significant advantage over regular public schools in central cities and urban fringes for reading and in urban fringes for mathematics. Once race and poverty are taken into account, the advantage disappears — for mathematics the charter school effect is mostly negative, though the difference is statistically insignificant.
Robustness checks — using alternate weights and fixed effects estimation
Hoxby’s results do not seem to be robust to the use of alternate weighting procedures or a fixed effects estimation strategy (see Appendix B). When we do not weight the results, or weight them using the number of test takers in the public school (unlike Hoxby, who uses the number of test takers in the charter school as weights) — the estimates are often significantly different from Hoxby’s results. This implies that the charter school effect may vary depending on the size of the school. Further, when we correct for heteroscedasticity using a fixed effects formulation, we find no significant charter school advantage in math, even without controls. For reading the coefficient is positive and significant, though lower than Hoxby’s estimates, but this disappears when we control for racial composition and low-income status.
Conclusion
In “A Straightforward Comparison of Charter Schools and Regular Public Schools in the United States,” Caroline Hoxby argued that charter school students were 3.8% more likely to be proficient on their state’s reading exam when compared to students in the nearest public school. They were 4.9% more likely to be proficient when compared to students in the nearest public school with a similar racial composition. The corresponding “charter advantage” in math was 1.6% and 2.8%. But Hoxby’s method of matching schools based primarily on distance inadequately controls for differences in racial composition and socioeconomic status. When one directly takes into account racial composition and poverty (proxied by free and reduced-price lunch eligibility), the perceived advantage of charter schools vanishes. In math, in fact, the coefficient becomes negative in some cases, though it is not statistically significant.
This is true not only for the U.S. as a whole and most of the major charter states, but also for charter schools in different locales, e.g., central cities and rural areas.
In retrospect, this is perhaps not surprising. When Hoxby matches charter schools with their nearest public schools with a similar racial composition, instead of matching them with just the nearest public schools, the charter school advantage appears much larger. For example, in reading the estimate increases from 3.8% to 4.9% (an increase of about 30%), and in mathematics the increase is from 1.6% to 2.8% (an increase of about 75%). This is despite the fact that only about 8% of the schools differ between the two samples. That such a large change occurs by switching such a small number of schools in the sample underscores the importance of adequately controlling for racial composition and similar background variables — the results are likely to be seriously biased otherwise.
A cross-sectional study such as this one has its limitations, particularly in assigning causality based on the estimates. As is now widely accepted, the ideal way to determine effectiveness of policy changes or reform proposals is to randomize across students, and then follow the treatment and control groups over time. However, it is difficult to randomize on a large scale, and results can be sensitive to students leaving the study population as it progresses from year to year. It is often difficult even to gather longitudinal data on students by following the same students over time, and the problem of selection may not be satisfactorily resolved by a simple tracking of students over time. In the absence of adequate randomized trials and panel data, careful cross-sectional studies can often throw up interesting insights and alert us to potential problems and solutions, particularly when the sample is large and diverse enough. But their ability to expand our particular knowledge of what works and what doesn’t in education is severely limited.
We are grateful to Prof. Caroline Hoxby for generously sharing her dataset with us. We are also grateful to her secretary, Trina Ott, for assistance in this regard. We received helpful comments and suggestions from Jack Buckley, Martin Carnoy, Helen Ladd and Jonah Rockoff. This study has also benefited from the advice of Eileen Foley and our other colleagues at the Economic Policy Institute, too numerous to mention individually. In addition, Patrick Watson and Joseph Procopio, our editors, were of tremendous help during the publications process. We alone remain responsible for all remaining errors.
— April 2005
Appendix A: Methodology for measuring the charter school effect
The first step in assessing the effect of charter schools for reading and math proficiency is to run weighted least squares regressions on the proficiency difference between a charter school and its matched regular public school. As in Hoxby, we use the following regression:
![]()
where ![]() is the difference in proficiency between the charter school and its matched public school in match-group j,
is the difference in proficiency between the charter school and its matched public school in match-group j, ![]() =difference in values of the other regressors, defined below and similarly differenced, and
=difference in values of the other regressors, defined below and similarly differenced, and ![]() is the error term. (Specifically, yjk is the percentage of students at school k in match-group j scoring at or above the proficient level, k={public, charter}. Note that, because of the differencing within each match-group, each of the match-groups, which consists of one charter school and its matched regular public school, generates one observation. (This has implications for weighting, as discussed later.) The constant term will give an estimate of the charter school advantage. If no other regressors are included, this is just the average of the charter school proficiency across all matched pairs. The inclusion of additional covariates (measures of student characteristics) yields the charter school effect net of the effect of student backgrounds. The subsequent analysis includes controls for the racial composition and the low-income status of students in the schools. In particular, we control for the difference between the charter school and its matched regular public school in the percentage of students who are American Indian, Asian, Hispanic, or black (the percentage of students who are white is the omitted category) and in the percentage of students who are eligible for free or reduced-price lunch programs.
is the error term. (Specifically, yjk is the percentage of students at school k in match-group j scoring at or above the proficient level, k={public, charter}. Note that, because of the differencing within each match-group, each of the match-groups, which consists of one charter school and its matched regular public school, generates one observation. (This has implications for weighting, as discussed later.) The constant term will give an estimate of the charter school advantage. If no other regressors are included, this is just the average of the charter school proficiency across all matched pairs. The inclusion of additional covariates (measures of student characteristics) yields the charter school effect net of the effect of student backgrounds. The subsequent analysis includes controls for the racial composition and the low-income status of students in the schools. In particular, we control for the difference between the charter school and its matched regular public school in the percentage of students who are American Indian, Asian, Hispanic, or black (the percentage of students who are white is the omitted category) and in the percentage of students who are eligible for free or reduced-price lunch programs.
The implicit assumption behind this methodology is that, if the students currently attending charter schools were to attend their nearest regular public school instead, their average score would be equal t
o the average score of the students currently attending those public schools. So a straightforward comparison of proficiency levels between charter schools and their matched regular public schools yields a measure of charter schools’ average proficiency advantage. Hoxby’s original paper (Hoxby 2004a) includes no controls for racial composition (other than matching schools on that basis) or low-income status (subsidized lunch eligibility). In the revised version (2004b), Hoxby argues that “matching is a superior statistical method because it does not rely on unrealistic assumptions about linearity,” and says that “an example of such an unrealistic assumption is that being Hispanic always has the same effect on a student’s achievement, regardless of whether he lives in South Texas, Miami, or Minnesota!” While this assertion would be true if the matching exercise generated schools that were very similar in observable characteristics within each group, the summary statistics in Table 1 do not support it. Further, because we run separate regressions for each of the larger states — including Texas, Florida, and Minnesota — we do not have to make the assumption that being Hispanic always has the same effect on a student’s performance. On the other hand, by not controlling for differences in racial composition, the implicit assumption is that the matching methodology adequately controls for race and ethnicity.
Note that we do have to assume that racial composition and free lunch eligibility affects performance linearly within a state. Matching is considered an improvement over regression-type adjustment in certain circumstances since in the former we do not have to rely on some implicit out-of-sample comparisons. However, this is true only when we can be fairly certain that the matched pairs are very similar and will lead to valid causal inference. A common way to increase the reliability of matching is to match observations on multiple dimensions using a summary score such as the propensity score or the Mahalanobis metric. See Buckley and Schneider (2003) for an example related to charter schools in Washington D.C. In future work it will be interesting to see what happens if we increase the sample size of the current study to include multiple public schools for each charter school, and then choose among the competing public schools based on multiple dimensions like distance, race, income, size, etc.
Table A-1 shows racial compositions across grades 2-5.


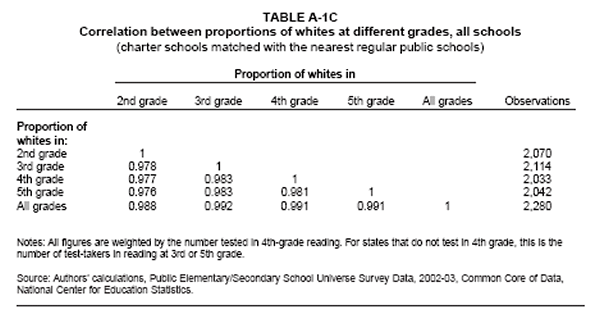
Table A-2 summarizes the proficiency differences between charter schools and their matched regular public schools. For the nation as a whole, 54% of the charter schools, accounting for about 61% of the charter school students in the sample, outperformed their counterparts in reading. The relevant figures for mathematics are 48% and 54%, implying that while a (small) majority of the charter schools scored lower than the matched regular public schools, a majority of the charter school students belonged to schools that scored higher. Looking at both subjects together, 40% of the charter schools had higher average proficiency levels in both reading and mathematics — a number almost equal to the percentage of charter schools (37%) that performed worse in both subjects. However, because the better charter schools are also those with relatively higher enrollments, 47% of the charter school students belonged to schools in the former category while 31% belonged to those that were outperformed in either subject.

Among the individual states, the charter advantage generally appears to be larger in reading than in mathematics, sometimes by significant margins, e.g., California, Ohio, Pennsylvania, and Texas. Wisconsin is the only state where there is a significant difference in the other direction. Note that these summary statistics do not control for differences in student characteristics that, as seen in Table 1, can be quite large and hence consequential.


Tables A-3A and A-3B show proficiency differences between charter schools and regular public schools focusing on the distance sample. Table A-4 shows the distribution of charter schools by locales. Table A-5 combines these locales to examine the charter school effect using the distance sample.


Appendix B: Robustness checks — using alternate weights and fixed effects estimation
An examination of the robustness of the results in Hoxby’s study using alternate weighting procedures and a fixed effects estimation strategy finds that charter schools’ estimated proficiency advantage often differs significantly across the different specifications.
Our first step is to run regressions of equation (1) in Appendix A without using any weights. The coefficient on the constant in this case indicates the expected proficiency difference between a charter school and its matched public school if one were to randomly draw a match-group from the sample. Next we weight the results by the number of test takers in the charter school.36 Here the estimate of the constant indicates the improvement that a randomly drawn charter school student has by attending his particular charter school (as compared to the matched public school that he might otherwise have attended). In this case, which is the weighting scheme that Hoxby uses, the results will be representative of the charter school student population. Finally, we weight the results by the number of test takers in the respective public schools. Here the coefficient can roughly be interpreted as the proficiency gain a randomly drawn public school student might have by attending the (matched) charter school. Now the results are representative of the public school students whose schools are located close to a charter school.37
In technical terms, ignoring the heteroscedasticity issue, and assuming that the difference in proficiency rates between each charter and its matched public school is an unbiased estimate of that charter’s treatment effect, weighting by the number of test takers in the charter school gives the effect of the treatment on the treated — the average treatment effect (proficiency gain) experienced by students who are currently attending charter schools. Weighting by the number of test takers in the public school gives the effect of the treatment on the untreated — the average treatment effect that would be experienced if all the students who now attend the matched public schools transferred to the corresponding charters.38
However, the more important concern in this context seems to be measurement problems in the dependent variable (i.e., sampling error-induced heteroscedasticity). One way to correct for this involves weighting a school’s proficiency by its respective enrollment (number of test-takers in this case) — public school proficiency by the public school enrollment and charter school proficiency by the respective charter school enrollment.39 Fixed effects regression, where we compare
the average proficiencies within each match-group, allows us to do so. Specifically, we assign a fixed effect to each match-group and then compare the within-group differences across the match-groups. These results are reported after the regressions that experiment with alternate weights. The fixed effects estimator is the most efficient estimator of a constant treatment effect, and should be preferred to weighting by the number of test takers in either the charter school or the public school if the goal is to adjust for heteroscedasticity.40
Table B-1 reports the coefficients from regressions that use alternate weights. The first three columns are for reading proficiency, the next three are for mathematics. In the first column under each subject we report results from regressions where we do not weight the regressions. Intuitively, this yields the simple average of the charter school proficiency advantage. In the next column we weight the regressions by the number of test takers in the charter school. In effect this simply replicates Hoxby’s estimates, and the numbers are identical to those in the second column of Tables 3A and 3B, respectively. Finally, in the third column we weight by the respective public school enrollment.

Consider first the results for reading. As is evident, many of Hoxby’s estimates are not robust to using alternate weights. If the results are not weighted, then the charter advantage at the national level drops by more than half, though it still remains significant at the 5% level. This implies that, while the larger charter schools are performing better than their public school counterparts, the smaller charter schools are performing disproportionately worse.41 If we use public school enrollment as the weighting variable, the charter coefficient is only marginally significant, and the proficiency advantage shrinks to just over 1. This suggests that the charter schools that are closer to larger public schools are the ones that are performing poorly.42
Looking at individual states, in states like Alaska, California, Illinois, Louisiana, Massachusetts, New Jersey, and Nevada using alternate weights does not change the results much. In states like Wisconsin (and Idaho), the estimated charter advantage actually increases when we use different weights.43 However, in some of the major charter states there are significant differences when the regressions are alternatively weighted or not weighted at all. The largest declines occur for states like Colorado and Hawaii, implying that some or most of the perceived charter advantage in these states may be coming from a small number of highly performing charter schools, which may not be representative of the average charter school in these states. While not as dramatic, there is a significant drop in the charter school coefficient in some other states as well — in Arizona, Florida, Georgia, and Pennsylvania the coefficient is only marginally significant, if at all, in the alternate specifications. In states like North Carolina, New York, Ohio, and Texas (and to some extent Michigan too), the already negative coefficient in Hoxby’s formulation becomes more negative and often significant while applying different weighting procedures.
A similar picture emerges when looking at the results for proficiency in mathematics. Here the coefficient actually becomes negative (and significant too, when weighted by the number of test takers in the public school).44 Most of the individual states follow the same pattern as in reading, though in Hawaii, for example, the decline in charter advantage is not as dramatic.
Table B-2 shows the results for the distance sample. This mirrors the patterns evident in Table B-1, though now the (overall) advantage of charter schools in reading is lower and insignificant. In mathematics, the coefficient changes sign, and the perceived disadvantage of the charter schools seems larger than it does in the race sample.

Fixed effects estimates
Table B-3 shows the estimates for the fixed effects regressions using the race sample; Table B-4 uses the distance sample. Here each school is weighted by the number of test takers in that particular school, a method that arguably provides a better correction for heteroscedasticity. The first four columns are for reading, the last four are for mathematics. The first column under each subject reproduces the Hoxby estimates. For states where she did not report the coefficients — because of statistical insignificance — we have added our own estimates from the second columns of Tables 3A and 3B. Not surprisingly, the results of the fixed effects regressions where we do not weight the observations are almost identical to those reported in the first and fourth columns of Table B-1 (OLS without weights). For brevity these are not reported.45
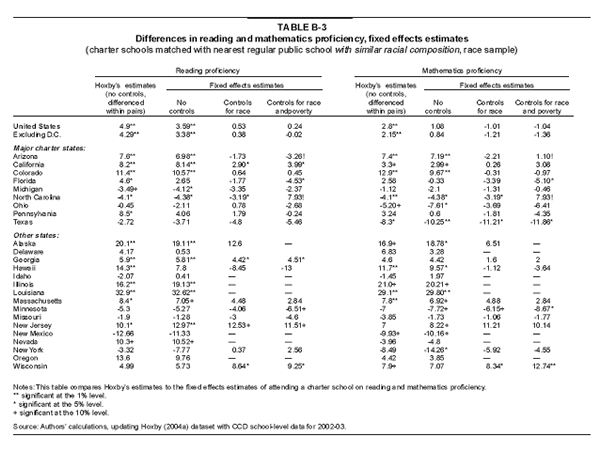

Looking at Table B-3 for reading, charter schools seem to maintain a significant advantage over their matched counterparts, comparable to Hoxby’s estimates, as long as we do not introduce any additional controls. When we do control for race or for race and income, the coefficient is only marginally above zero and becomes statistically insignificant. Only California among the charter-important states has a positive and significant charter advantage. In fact, the coefficients for the other large states are mostly negative (Arizona, Florida, Michigan, Texas) or barely positive (Ohio, Pennsylvania, Colorado).
The picture is similar for mathematics, though now a charter school advantage is even harder to find. Just running a fixed effects regression reduces the charter coefficient to less than half and makes it statistically insignificant from zero. Further controlling for race and for race and poverty makes the coefficients negative, though they are generally not significant. None of the larger states has a positive and significant charter advantage now, including California — the only state to do so in the entire sample is Wisconsin, which has about 27 schools. Like in reading, for most of the states the estimated effect of charter schools is negative (Arizona, Colorado, Florida, Michigan, Ohio, Pennsylvania, and Texas).
To summarize, Hoxby’s estimates of charter school proficiency advantage is not robust to alternative weighting strategies, and is not sustained when there are controls for observable differences in school socioeconomic composition. Using alternate weights often changes the results significantly and, perhaps more importantly, including student background characteristics as additional covariates neutralizes the apparent charter school advantage.
Endnotes
1. NAEP is a congressionally mandated project of the National Center for Education Statistics within the Institute of Education Sciences of the U.S. Department of Education. Its full written report on charter schools, America’s Charter Schools: Results From the NAEP 2003 Pilot Study, was published in December 2004 and is available online at http://nces.ed.gov/nationsreportcard/pdf/studies/2005456.pdf. The AFT study, Charter School Achievement on the 2003 National Assessment of Educational Progress, by F. Howard Nelson, Bella Rosenberg, and Nancy Van Meter, is available online at http://www.aft.org/pubs-reports/downloads/teachers/NAEPCharterSchoolReport.pdf. The
AFT results are very similar to those reported in the published NCES report.
2. Hoxby writes: “Because charter schools are highly unusual and idiosyncratically distributed, the NAEP sample of charter school students is unusual and idiosyncratically distributed&.Crude comparisons using NAEP data inevitably include inappropriate public school students in the control group” (Hoxby 2004a, endnote 5). Hoxby also argues that, because charter schools enroll only about 1.5% of students at the national level, it is important to include nearly all of them in an analysis, which her study does and which the NAEP data, being a sample of charter students, does not. Note however that the NAEP data have detailed information at the individual level on performance, student characteristics, parental background, etc. The Hoxby study, and this reanalysis, instead has to rely on comparisons among school aggregates rather than among individuals.
3. In states that do not test in fourth grade, she used third- or fifth-grade achievement.
4. Texas charter students were significantly less proficient in math, but not in reading.
5. Professor Hoxby recently published a revised and expanded version of the above study (Hoxby 2004b). However, because the revised study, like its predecessor, does not explicitly control for race and poverty in the proficiency regressions, the results are liable to be biased as in the former study.
6. Alternate corrections for heteroscedastic standard errors in schools’ proficiency measures yield lower estimates of charter advantage, as do allowing for heterogeneous treatment effects — even without controlling for race and low-income status.
7. In these four states the difference in the percentage of whites between the two types of schools is less than 6 percentage points (the difference in the percentage of non-Asian minorities between the two types of schools is less than 8 percentage points), and the difference in the percentage of students eligible for free lunch programs is less than 15 percentage points.
8. Note that because of the small sample sizes it is not possible to control directly for race and socioeconomic status in the regressions for Louisiana, Nevada, and other states with a small charter school presence.
9. See, e.g., the section on charter schools in Loveless (2002).
10. The dataset containing data on the charter schools and their matched public schools was provided by Hoxby. The authors are grateful to Professor Hoxby and her secretary, Trina Ott, for quick access to and help with these data.
11. There are 1,153 charter schools in all, and each is matched to a neighboring regular public school. Each charter school and its matched regular public school constitute a match-group. Thus, there are 1,153 different match-groups in each sample.
12. CCD data are publicly available at http://www.nces.ed.gov/ccd/pubschuniv.asp.
Though data on free and reduced-price lunch eligibility are available only at the overall school level, data on racial composition are available for each grade. However, the number of missing observations is often substantial at the grade level. Since racial compositions are highly correlated across grades, we mostly focus on the school-level breakdown. See Appendix Table A-1 for these correlations across grades 2-5. This table also shows that, out of the 2,306 schools in the sample, data on racial breakdowns are available for 2,280 (99%) if we look at the overall school-level distribution. However, if we look at a particular grade, say the fourth grade, we have 2,033 observations, a loss of about 250 observations (11%).
The school year 2002-03 is the last for which CCD data are available. Most of the data we use are at the school level, and year-to-year changes in demographic composition at the school level should not be large. So it should make little difference that we use 2002-03 data on racial composition and free lunch eligibility instead of 2003-04 data, even though the proficiency data for many of the states are for 2003-04.
13. The schools reporting zero free lunch eligibility are geographically clustered. Out of the 180 charter schools, 67 are in California, 55 in North Carolina, and 23 in Pennsylvania. Most of the regular public schools (12 out of 16) are in North Carolina.
If some of these charter schools reporting zero eligibility indeed have a free-lunch-eligible population, not accounting for it will yield a downward-biased estimate of the charter school effect. This is because, in general, free lunch eligibility is negatively correlated with performance.
14. Alaska has 16 charter schools, but, while this number would permit controlling for racial composition, we cannot control additionally for free lunch eligibility since such data are missing for most of the schools. Free lunch data are also missing from a significant number of schools in Arizona and North Carolina.
15. In Hoxby’s initial study the proficiency advantage for charter schools in Washington D.C. was particularly large — 35-36 points for reading and 40-42 points for math. So omitting D.C. from the regressions reduces the average advantage of charter schools at the national level. Assuming that the charter schools in D.C. do indeed have an advantage over their regular counterparts (as reported in Hoxby 2004b), excluding D.C. should give us a downwardly biased estimate of “true” charter school advantage, while including D.C. would give us an upwardly biased estimate.
16. The details are available on the website of the North Carolina State Board of Education, at http://www.ncpublicschools.org/accountability/reporting/2004memo/composite04.pdf. This use of a performance composite rather than actual proficiency levels is the reason why Hoxby’s results for reading are identical to those for mathematics in North Carolina; see Tables 2 and 3 in Hoxby (2004a). The actual fourth-grade reading and mathematics scores for 2003-04 are available on the state education department’s website at http://disag.ncpublicschools.org/2004/.
17. Bifulco and Ladd (2004) found that students in North Carolina charter schools made considerably smaller achievement gains than they would have in nearby traditional public schools.
18. Hoxby argues that the nearest regular school should be an adequate control group since we are looking at elementary grades (3-5), and at this level parents are generally wary of sending their children to schools far from home. While the latter part is undoubtedly true, confining oneself to the single nearest school may not be appropriate, particularly in larger cities when there can be multiple neighborhood schools with varying levels of reputation and achievement.
19. In the main section of the paper we report the results only for the race sample, where the comparison public school is the closest one with a similar racial composition. Most of the corresponding tables for the distance sample, where charter students are compared to their peers in the nearest public school, can be found in Appendix A
20. Hoxby reports that for the distance sample, compared to students in the nearest regular public school, charter schools’ fourth-graders are 2.4% more likely to be black, 1.0% less likely to be Asian, and 8.0% less likely to be Hispanic (Hoxby 2004a, endnote 13). This is broadly in line with the figures here, though they show that charter school students are even more likely to be black.
21. Examination of the characteristics of the neighborhoods of the omitted charter schools suggests that the 15-point gap may be an under-estimate of the true difference between the two types of schools, but it is difficult to be exact about this. We computed the
percentage of students eligible for free or reduced-price lunches in regular public schools belonging to match-groups where such data were available for both types of schools. We then compared this number to the corresponding number in regular public schools belonging to match-groups where such free lunch data were unavailable (or reported to be zero) for the matched charter school. The respective figures were 64% and 51%. This suggests that the match-groups left out when we control for free-lunch eligibility serve somewhat more advantaged student bodies than the ones included, and that some of the reported zeroes can indeed be the true free-lunch eligibility numbers for the corresponding schools.
22. Hoxby writes, “Charter schools that are small or recent start ups tend not to participate in the lunch programs even if some of their students are eligible” (Hoxby 2004a, endnote 13). She argues that free and reduced-price lunch programs measure participation, not the eligibility of students, and hence can yield misleading statistics. In this analysis we have restricted the free lunch statistics to only those schools that report a non-zero number. The CCD survey questionnaire for 2002-03, available online at http://nces.ed.gov/ccd/pdf/psu02form.pdf, asks schools about their students’ eligibility, not participation in an actual program, but it is possible that there are errors in reporting. Note that the statistics will be biased only if the reporting errors are greater for charter schools than the matched regular public schools.
23. These statistics for Arizona are in line with those of Dee and Fu (2004), who concluded that the introduction of charter schools in Arizona increased pupil-teacher ratios in traditional public schools by 6% and reduced the proportion of white non-Hispanic students by 2%.
24. In Ohio, though, public schools have a somewhat higher percentage of poor children.
25. Because the number of charter schools in the sample from Louisiana and Nevada is small (seven and five, respectively), we are not able to estimate proficiency differences while controlling for race and income.
26. A match-group is considered to be in one location, say central city, if the charter school in that match-group is located in a central city. For most of the match-groups, both the charter school and the matched regular public school fall in the same locale (or at least in the same category defined above). For example, for the 597 charter schools located in central cities, 562, or more than 94%, of the matched regular public schools are also located in central cities.
27. In Arizona, 58% of the charter schools in the sample are located in a central city. The respective figures for other states are California 45%, Colorado 27%, Florida 33%, Michigan 50%, North Carolina 38%, Ohio 82%, and Texas 77%. In Colorado and Florida, most of the charter schools in the sample are in urban fringe areas (45% and 55%, respectively). Recall that the sample consists of all charter schools in a state offering a fourth grade.
28. Overall, central city charter schools serve a marginally lower proportion of non-Asian minorities than do their matched regular public schools, 70% to 73%.
29. The NAEP study found that, although charter schools are much more likely than regular public schools to locate in a central city (50% to 29%), overall they serve a slightly smaller proportion of students eligible for free or reduced-price lunches (42% to 44%). (This study compares charter school students to a random sample of all public school students.) This suggests that central city public schools serve a somewhat higher proportion of low-income students than do central city charter schools, since public schools located in central cities are likely to serve more disadvantaged children than do public schools in other locations.
30. Conversely, in states like North Carolina and Texas, charters serve a much higher percentage of black students.
31. As mentioned above, we focus here on the results for the race sample. The results for the distance sample can be found in Appendix Tables A-3A and A-3B.
32. Hoxby (2004a) reports results at two different levels of statistical significance — 10% and 1%. We use three levels — 10% (+), 5% (*), and 1% (**). Thus, in some of the cases the exact significance levels in the first column may differ from those in Table 2 in Hoxby (2004a).
33. The results in the first row include the faulty statistics for Washington D.C., so these are slightly biased upward. The second row omits D.C. altogether. Since in the latest study Hoxby finds some proficiency advantage for charter schools in D.C., the true effect should lie somewhere in between.
34. For most of the states, and for the United States as a whole, the difference between the smaller and the larger sample is small. As is seen when comparing the last two columns, the decline in the estimated value of charter advantage is due to controlling for poverty and not due to using a different sample. (Some of the exceptions include Ohio, Pennsylvania, etc.)
35. For regressions that include separate dummies for each of the eight different locales, the results are broadly similar to those in Table 4. Initially, only locale 1 (large city) and locale 3 (urban fringe of a large city) seem to have a significant charter advantage in either reading or mathematics. Controlling for race and poverty, however, only locale 3 still has a comparative advantage, though this is significant only in reading. It is interesting to note that, while charters in locales 1 and 3 seem to perform relatively better, those in locales 2 and 4 (mid-size city and urban fringe of a mid-size city — conceptually quite close to locales 1 and 3) seem to do quite poorly, sometimes significantly so.
36. The number of test takers in the charter schools in the sample ranges from a minimum of one to a maximum of 313, with a mean of 43 and a standard deviation of 38. The number of test takers in the public schools range from four to 423, with a mean of 80 and a standard deviation of 45.
37. For illustration, consider a state with two charter schools, one small and near a large public school, the other large and near a small public school. The unweighted estimate gives the average of the two charter schools’ proficiency advantages. Hoxby’s approach, i.e., weighting by the charter school enrollment, essentially gives the advantage of the second charter school, while the public-school-weighting gives in effect the advantage of the first charter school. Of course, if the effects are the same — that is, relative charter school proficiency is the same in either case — then all the three methods give identical results.
38. Strictly speaking the last point is not correct. If we want to estimate the “true” effect of the treatment on the untreated we have to do the matching in reverse, i.e., assign charter schools to public schools instead of the other way around. But the above should give a rough idea of the magnitude of this effect.
39. Another way to correct for heteroscedasticity is to compute Huber-White robust standard errors. But this only changes the standard errors on the coefficients, and not the coefficient estimates themselves. Generally this increases the standard errors, so as to make coefficients that earlier were significant insignificant. Since we have only a small number of significant coefficients, we have refrained from using robust standard errors — the results are unlikely to be any different.
40. Hoxby’s dependent variable is the difference in proficiency between a charter school and its matched public school (differenced within a match-group), so each match-group generates one observation and can be weighted by either the number of test-takers in the public school or the number of t
est-takers in the charter school. Hoxby argues that since charter schools are much smaller compared to the regular public schools, a first correction for heteroscedasticity should be weighting the dependent variable (difference in proficiency) by the number of test-takers in the charter school.
41. A similar finding, that larger charter schools score higher than smaller charter schools, was reported by Tom Loveless in the 2002 Brown Center Report on American Education, mentioned earlier. Loveless argues that this might be related to school administration, and that economies of scale may play an important part. Another explanation for this may be that it is the better charter schools that expand over time. Unfortunately, the data at hand do not permit any detailed examination of this issue at present.
42. This is intriguing, though it is not obvious why this should be so.
43. This is also true of a few smaller states like Missouri and New Mexico, where the charter disadvantage actually goes down for regressions using alternate weights.
44. This is not surprising, since as Appendix Table A-2 shows, in a small majority of the match-groups it was the public school that outperformed its charter school counterpart in mathematics. For the U.S. as a whole, 47% of the charter schools scored higher than their matched regular public schools. (However, a majority of charter school students (53%) attended schools that scored higher than their matched regular public schools.)
45. We have dropped the match groups where either the charter school or the regular public school had missing values for proficiency or enrollment. There are 13 schools (10 charter and three public) with missing values for reading proficiency, though none has a missing value for math proficiency (two schools have a value greater than 100). Nineteen schools (15 charter and four public) have a missing value or zero for number of test-takers in reading; all but two of them, one charter and one regular public school, have missing values for the number of test-takers in math as well. When running the regressions with controls, we have dropped the match groups where at least one of the schools has missing values for these controls.
Bibliography
Bifulco, Robert, and Helen F. Ladd. 2004. The Impacts of Charter Schools on Student Achievement: Evidence From North Carolina. Durham, N.C.: Sanford Public Policy Institute, Duke University.
Buckley, Jack, and Mark Schneider. 2003. “Making the Grade: Comparing D.C. Charter Schools to Other D.C. Public Schools” Educational Evaluation and Policy Analysis, 25(2).
Dee, Thomas, and Helen Fu. 2004. “Do Charter Schools Skim Students or Drain Resources?” Economics of Education Review, 23.
Dobbs, Michael. 2004. “Charter vs. Traditional: Two Types of D.C. Public School Are Not Easy to Compare.” Washington Post, December 15, p. B01.
Hoxby, Caroline. 2004a. “A Straightforward Comparison of Charter Schools and Regular Public Schools in the United States.” Mimeo. Harvard University, September. Available at http://post.economics.harvard.edu/faculty/hoxby/papers/charters_040909.pdf.
Hoxby, Caroline. 2004b. “Achievement in Charter Schools and Regular Public Schools in the United States: Understanding the Differences.” Mimeo. Harvard University, December. Available at http://post.economics.harvard.edu/faculty/hoxby/papers/hoxbycharter_dec.pdf.
Loveless, Tom. 2002. How Well Are American Students Learning? Brown Center Report on American Education. Washington, D.C.: Brookings Institution. Available at http://www.brookings.org/dybdocroot/gs/brown/bc_report/2002/bcr_report.pdf.
Schemo, Diana Jean. 2004. “Nation’s Charter Schools Lagging Behind, U.S. Test Scores Reveal.” New York Times, August 17.
